Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы сложения скоростей и ускорений ⇐ ПредыдущаяСтр 3 из 3
Теорема сложения скоростей Для установления зависимостей между абсолютными, относительными и переносными скоростями и ускорениями точки будем предполагать, что подвижная система отсчета Axryrzr движется поступательно вместе с полюсом А, и совершает вращение вокруг мгновенной оси АР с угловой скоростью ω е и угловым ускорением ε е переносного движения (рис. 2.26).
Рис.2.26
Движение точки М относительно системы Axryrzr задано с помощью радиус-вектора
Запишем:
где Продифференцируем соотношение (2.73) с учетом (2.74) по времени:
В соответствии с определением скорости, Производные по времени от вращающихся геометрических векторов постоянной длины есть скорости движения их концов, которые определяются в соответствии с формулой (2.51):
Таким образом, второе слагаемое в правой части (2.75) приобретет вид:
В последней форме записи (2.77) поступательные и вращательные скорости переносного движения объединены в соответствии с (2.70) в общую скорость Итак, сформулируем теорему сложения скоростей (2.77): вектор абсолютной скорости точки при сложном движении равен геометрической сумме ее переносной и относительной скоростей. Теорема сложения ускорений Если продифференцировать по времени полученное уравнение (2.77), то можно получить выражение, связывающее ускорения в неподвижной и подвижной системах отсчета. Оно носит название теорема о сложении скоростей, или теорема Кориолиса. Опустив необходимые преобразования, сформулируем ее в окончательном виде:
Абсолютное ускорение точки при сложном движении является векторной суммой трех ускорений – переносного, относительного и ускорения Кориолиса.
В формулировке теоремы обозначены: · · · ·
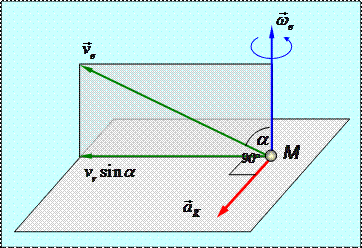
Рис.2.27 Ускорение Кориолиса определяется по следующей формуле:
Ускорение Кориолиса есть удвоенное векторное произведение вектора угловой скорости переносного движения на вектор относительной скорости. Как видно из определяющей формулы (2.79), вектор ускорения Кориолиса зависит как от угловой скорости переносного движения, так и от относительной скорости точки. Его величина определяется выражением:
Из формулы следует, что это ускорение будет отсутствовать при
Рис.2.28 Направление вектора ускорения Кориолиса определяется по правилу векторного произведения (рис. 2.28).
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое абсолютные, относительные и переносные движения, скорости и ускорения точки? 2. Сформулируйте теоремы о сложении скоростей и ускорений при сложном движении точки. 3. Как определить направление и величину ускорения Кориолиса?
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.200.66 (0.009 с.) |

 , а относительно неподвижной системы отсчета – с помощью радиус-вектора
, а относительно неподвижной системы отсчета – с помощью радиус-вектора  . Движение начала подвижной системы отсчета А относительно неподвижной системы Oxyzопределяетс я радиус-вектором
. Движение начала подвижной системы отсчета А относительно неподвижной системы Oxyzопределяетс я радиус-вектором  . Очевидно:
. Очевидно: .
.
 ,
,
 - орты подвижных осей координат.
- орты подвижных осей координат. .
.
 – абсолютная скорость точки М;
– абсолютная скорость точки М;  – скорость начала (т. А) подвижных координат или скорость точки Мпри переносном поступательном движении,
– скорость начала (т. А) подвижных координат или скорость точки Мпри переносном поступательном движении,  - относительная скорость точки М.
- относительная скорость точки М. .
.
 - это скорость точки Мпри переносном вращательном движении с угловой скоростью ω е. Тогда выражение (2.75) можно записать в виде:
- это скорость точки Мпри переносном вращательном движении с угловой скоростью ω е. Тогда выражение (2.75) можно записать в виде: .
.
 .
. .
.
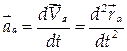 - вектор абсолютного ускорения;
- вектор абсолютного ускорения; - вектор переносного ускорения, имеющий поступательную
- вектор переносного ускорения, имеющий поступательную  , вращательную
, вращательную 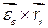 и осестремительную
и осестремительную  составляющие, в соответствии с (2.72);
составляющие, в соответствии с (2.72); - вектор относительного ускорения, который в соответствии с (2.20), (2.21) и (2.27) можно расписать в декартовых и естественных осях подвижной системы координат;
- вектор относительного ускорения, который в соответствии с (2.20), (2.21) и (2.27) можно расписать в декартовых и естественных осях подвижной системы координат; - т.н. «поворотное» ускорение, названного в честь французского механика Густава Гаспара Кориолиса (1792 – 1843 г.г.), рис.2.27.
- т.н. «поворотное» ускорение, названного в честь французского механика Густава Гаспара Кориолиса (1792 – 1843 г.г.), рис.2.27.
 .
.
 .
.
 = 0,
= 0,  = 0, илипараллельности векторов
= 0, илипараллельности векторов  и
и  .
.