
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика абсолютно твердого телаСтр 1 из 3Следующая ⇒
Как уже отмечалось во введении, в абсолютно твердом теле сохраняется неизменным расстояние между любыми его точками, как бы само тело ни перемещалось. Это означает, что точки абсолютно твердого тела движутся согласованно. В этом параграфе будут рассмотрены законы этих согласованных движений точек для различных случаев движений самих абсолютно твердых тел.
Поступательное движение Поступательным называют такой вид движения абсолютно твердого тела, при котором прямая, проходящая через любые две точки тела, движении остается параллельной самой себе. Иными словами, при поступательном движении пространственная ориентация тела не меняется. Примеры поступательного движения тел: ступенька в движущемся эскалаторе, кабина в колесе обозрения.
Рис. 2.10 Пусть некоторое тело, в котором выделены точки А и В перемещается поступательно (рис.2.10). При таком движении, согласно определению, отрезок АВ не меняя пространственную ориентацию, перемещается в новое положение А′В′. Положения точек А и В в пространстве определяются радиус-векторами
Поскольку отрезок Продифференцируем (2.33) по времени:
Поскольку отрезок
Очередное дифференцирование (2.34) приводит к равенству ускорений рассматриваемых точек:
Поскольку А и В – произвольно выбранные в теле точки, то из предыдущего следует, что при поступательном движении все точки абсолютно твердого тела двигаются по одинаковым траекториям и имеют равные скорости и равные ускорения в любой момент времени. В этих условиях для описания поступательного движения тела достаточно знать, как движется хотя бы одна его точка, что сводит задачу к уже рассмотренной выше кинематике материальной точки.
Как будет следовать из анализа других видов движений твердого тела, только поступательное движение обладает указанными свойствами. Это значит, что кроме поступательного, при всех других видах движения точки тела двигаются с различными скоростями и ускорениями. Таким образом, понятия «скорость тела» или «ускорение тела», движущегося не поступательно, не имеют смысла и их использовать некорректно.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Приведите еще примеры плоскопараллельного движения. 2. К чему приводится описание плоскопараллельного движения твердого тела?
Вращательное движение Вращение - это такой вид движения абсолютно твердого тела, при котором у тела есть две неподвижные точки. Прямая, проходящая через эти неподвижные точки, называется осью вращения тела.
Из геометрических соображении легко показать, что все точки абсолютно Рис 2.11 твердого тела, лежащие на оси вращения, также неподвижны. Пусть ось вращения тела связана с точками А и В (рис.2.11). Произвольная точка К абсолютно твердого тела может находиться на фиксированных расстояниях от точек А и В. Геометрическими местами точек, равноудаленных от них, являются сферы с радиусами АК и ВК соответственно. Их пересечение – окружность радиуса h, центр которой лежит на оси АВ. Таким образом, при вращении тела все точки тела описывают окружности с центрами, лежащими на оси вращения тела.
Скалярные характеристики вращательного движения
Угол поворота тела При повороте тела на некий угол φ произвольная точка К переместится вдоль окружности радиуса h по дуге
Путь, пройденный точкой тела при его вращении, равен произведению радиуса на угол поворота тела.
Здесь φ – угол поворота тела в радианах, определяет закон вращательного движения тела вокруг оси:
Угловая скорость вращения Продифференцируем (2.35) по времени, учтя, что радиус h постоянен:
Введем понятие угловой скорости вращения тела:
Угловая скорость есть производная по времени от угла поворота.
Размерность угловой скорости – радианы в секунду (рад/с). Поскольку радиан – безразмерная единица (определяется как отношение длины дуги окружности, равной радиусу, к самому радиусу), часто вместо радиана в размерности угловой скорости ω пишут единицу (1/с, или Тогда, используя (2.16), выражение (2.37) запишется в виде:
Алгебраическая скорость точки тела при его вращении равна произведению угловой скорости на радиус. Заметим, что направление вектора скорости, как и в общем случае движения точки по траектории, направлен вдоль касательной к траектории, а в нашем случае – по касательной к окружности, т.е. перпендикулярно радиусу (см. рис.2.11).
Угловое ускорение тела Снова продифференцируем по времени (2.40):
Введем понятие углового ускорения тела:
Угловое ускорение есть производная по времени от угловой скорости или вторая производная от угла поворота.
Размерность углового ускорения – радианы в секунду в квадрате (рад/с2), или 1/ с2, с-2).
Учтя (2.28) и (2.42), выражение (2.41) приобретет вид:
Касательное ускорение точки тела при его вращении равно произведению углового ускорения на радиус.
Выражение для второго компонента ускорения – нормального ускорение точки может быть получено с использованием (2.28) и (2.40), если в качестве радиуса кривизны ρ принять радиус окружности траектории движения точки h:
Окончательно:
Нормальное ускорение точки тела при его вращении равно произведению квадрата угловой скорости на радиус.
Полное ускорение точки, с учетом (2.29), (2.43) и (2.44), будет:
Угол μ между главной нормалью и полным ускорением
Из полученного результата (2.46) следует, что поскольку угол μ не зависит от выбора точки тела и его величина определяется только параметрами углового движения тела, то вектора полных ускорений точек вращающегося тела ориентированы по отношению к радиусам точек под одним и тем же углом. Изобразим графически полученные соотношения, рассматривая вращающееся тело со стороны оси вращения. Рисунки, на которых изображены вектора и указаны изменения при их приложении к различным точкам, называются планами или эпюрами. Угловые характеристики вращения тела – угол поворота φ, угловую скорость ω и угловое ускорение ε в таких случаях принято изображать в виде круговых стрелок вокруг оси вращения. Направления стрелок связано с положительной величиной соответствующего углового параметра (рис.2.12, а также 2.11).
Рис. 2.12 Вектора скоростей точек вращающегося тела направлены перпендикулярно радиусам и будут меняться пропорционально их величинам. План скоростей для точек вращающегося тела выглядит так:
Рис. 2.13 Вектора ускорений точек вращающегося тела направлены под углом μ к радиусам и будут меняться пропорционально их величинам. План ускорений для точек вращающегося тела выглядит так:
Рис. 2.14 ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Сформулируйте определения понятий «угловое перемещение», «угловое скорость» и «угловое ускорение» при вращательном движении тела. 2. Какими формулами определяется аналитическую связь между угловыми параметрами (φ, ω, ε) вращающегося твердого тела и кинематическими характеристиками движения его точек (s, V, a τ , a n , a)? 3. В какую сторону будет вращаться тело (рис.2.13), если его угловая скорость ω отрицательна?
Частные случаи вращательного движения 1) Угловое ускорение отсутствует (равно нулю) (ε= 0). Поскольку угловое ускорение определяется формулой (2.42) как производная по времени от угловой скорости и равна нулю, это означает отсутствие изменений угловой скорости во времени, т.е. она постоянна (ω = const). При постоянной угловой скорости путь угол меняется по линейному закону от времени. Такой вид движения носит название равномерное вращение тела и характеризуется следующими зависимостями от времени угловых характеристик:
где Следует отметить, что в технике широко применяются т.н. «технические» единицы измерения вращательного движения: число оборотов (N, об), скорость вращения (n, об/мин, либо об/с). Связь между угловыми и техническими единицами легко установить, исходя из соотношений между одним оборотом и радианом, минутой и секундой и сводится к следующим формулам:
2) Угловое ускорение – постоянная величина ( Из (2.42)следует, что поскольку угловое ускорение
Так же, как и при движении точки, различают равноускоренное вращение (ε > 0) и равнозамедленное движение (ε < 0). При равноускоренном вращении скорость равномерно нарастает, при равнозамедленном – падает.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Сформулируйте законы изменения углового перемещения, угловой скорости и углового ускорения при равномерном вращении тела. 2. Сформулируйте законы изменения углового перемещения, угловой скорости и углового ускорения при равнопеременном вращении тела.
3. В какую сторону будет вращаться тело (рис.2.13), если его угловая скорость ω отрицательна?
Векторные характеристики вращательного движения
Введенные в предыдущих параграфах скалярные параметры (угол поворота φ, угловая скорость ω и угловое ускорение ε) характеризуют вращательное движение тела, но обладают одним недостатком: они не несут в себе информацию о расположении и ориентации оси вращения тела. В скалярном рассмотрении это указывается отдельно. Можно придать этим характеристикам векторный характер, введя, например, вектора угловой скорости
 Рис.2.15 Рис.2.15
Проведем из точки О на оси АВ радиус-вектор Исследуем, что такое векторное произведение
Рис.2.16 Вектор
Продифференцируем обе части равенства (2.51) по времени:
Выражение
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Как определить величину и направление вектора скорости точки вращающегося тела, зная вектор его угловой скорости? 2. Как определить величину и направление вектора ускорения точки вращающегося тела, зная вектора его угловых скорости и ускорения? 3. Куда будет ориентирован вектор углового ускорения
Плоскопараллельное движение Плоскопараллельное движение – это такой вид движения, при котором точки абсолютно твердого тела движутся в плоскостях, параллельных друг другу. Многие звенья машин и механизмов совершают такое движение. например, качение колеса по прямолинейному рельсу, движение шатуна в кривошипно-ползунном механизме и т.д.
Закон плоскопараллельного движения Точки тела, лежащие на одном перпендикуляре к неподвижной плоскости H, имеют одинаковые траектории, скорости и ускорения, так как этот перпендикуляр движется поступательно. Следовательно, для изучения движений точек этого перпендикуляра, достаточно изучить движение одной из них, например М (см. рис.2.17), а значит, для изучения движения плоскопараллельного движения тела, достаточно изучить движение точек тела, лежащих в сечении тела плоскостью П, параллельной неподвижной плоскости H, т.е. движение плоской фигуры S.
Рис.2.17 Положение фигуры S в плоскости П определяется положением любого отрезка АМ (рис. 2.18), принадлежащего фигуре. В свою очередь, положение отрезка АМ задается координатами одной из его точек, например А, которую называют полюсом, и ориентационным углом
Рис. 2.18 Таким образом, для описания положение тела надо задать закон плоскопараллельного движения (или иногда говорят " плоского движения ") в виде функций:
при этом функции Отсюда следует, что плоскопараллельное движение можно рассматривать как совокупность (сумму) поступательного движения, при котором все точки тела движутся так же, как полюс А, и вращения тела вокруг оси, проходящей через этот полюс.
Скорости точек тела при плоском движении Определение скоростей через полюс Если в качестве полюса выбрать точку А, для любой другой точки тела (например, т. В) можно записать:
Продифференцируем это выражение по времени:
или
где ` Скорость движения точки В относительно полюса А определим по формуле для вращательного движения (2.40):
Естественно, вектор ` Таким образом, вектор скорости (
Рис. 2.19
Иллюстрацией такой формулировки служит рисунок 2.19, где векторное сложение
Определение скоростей через мгновенный центр скоростей (м.ц.с.) Мгновенный центр скоростей - точка P плоской фигуры, скорость `VP которой в данный момент времени равна нулю (VP =0).
Пусть такая точка существует. Тогда выражение (2.54) для точки P будет иметь вид:
При `VP = 0 должно быть:
Найдя такую точку и приняв ее за полюс, выражение (2.54) для произвольной точки С примет вид:
Формально отсюда следует, что скорость точки С и скорость движения (вращения) т. С относительно т. Р – одно и то же. Следовательно, скорости точек тела определяются, как если бы оно вращалось вокруг оси, проходящей через мгновенный центр скоростей (рис. 2.20). При этом скорости точек тела и расстояния от них до м.ц.с. определяется следующими соотношениями:
Рис. 2.20 Для определения положения мгновенного центра скоростей знать линии по которым направлены скорости двух любых точек А и В. М.ц.с. будет находиться на пересечении перпендикуляров к этим линиям. Для определения направления вращения фигуры необходимо знать направление вектора скорости одной из точек А или В. И, наконец, для определения величин скоростей других точек, согласно выражению (2.58), необходимо знать величину скорости одной из точек А или В. Так, например, при качении без проскальзывания колеса точка касания является мгновенным центром скоростей.
Определение скоростей по теореме о проекциях скоростей двух точек
Если спроецировать на прямую АВ скорости точек А и В (рис. 2.21, 2.22), определяемые векторным соотношением (2.54), то в силу перпендикулярности вектора  отрезку АВ его проекция будет равна нулю. отрезку АВ его проекция будет равна нулю.
Рис.2.21
Рис.2.22 Тогда после проецирования выражение (2.54) приобретет вид:
Сформулируем соответствующий вывод:
Проекции скоростей двух точек абсолютно твердого тела на прямую, проходящую через эти точки, равны.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое мгновенный центр скоростей? Как найти его местоположение? 2. Приведите формулировки трех рассмотренных приемов по определению скоростей точек тела при его плоскопараллельном движении. 3. Подумайте, как найти местоположение мгновенного центра скоростей в случае, если точки А, В и Р (рис.2.20) лежат на одной прямой?
Ускорения точек тела при плоском движении Определение ускорений через полюс Продифференцируем выражение (2.54) по времени:
Каждое из членов этого равенства представляет собой соответствующее ускорение, которое может быть записано кратко, в виде полного ускорения, так и в развернутом виде, через свои касательные и нормальные компоненты:
Вектор ускорения ( Следует отметить, касательные и нормальные направления в (2.60) каждого полного ускорения Иллюстрацией соотношений между векторами по (2.60) служит рис.2.23.
Рис. 2.23 Определение ускорений через мгновенный центр ускорений (м.ц.у.) Мгновенный центр ускорений - точка Q плоской фигуры, ускорение `
Используя подход, аналогичный примененному при рассмотрении мгновенного центра скоростей, можно так сформулировать основные результаты: · Мгновенный центр ускорений находится на пересечении прямых, проведенных к векторам ускорений точек абсолютно твердого тела под углами μ в направление углового ускорения ε (рис.2.24) ( · Ускорения точек тела определяются, как если бы оно вращалось вокруг оси, проходящей через мгновенный центр ускорений (т. Q, рис. 2.24). При этом ускорения точек тела и расстояния от них до м.ц.у. определяется следующими соотношениями:
Рис.2.24 Замечание Мгновенный центр ускорений (м.ц.у.) и мгновенный центр скоростей (м.ц.с.) – вообще говоря, разные точки. Они могут совпадать в отдельных случаях, например, при вращательном движении вокруг неподвижной оси. Так, в случае равномерного качении колеса без проскальзывания мгновенный центр скоростей (м.ц.с.) - это точка касания колеса опорной поверхности. Мгновенный же центр ускорений (м.ц.у.) – точка, совпадающая с движущимся центром колеса.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое мгновенный центр ускорений? Как найти его местоположение? 2. Сформулируйте методы определения ускорений точек тела при плоскопараллельном движении. 3. Подумайте, как найти местоположение мгновенного центра ускорений в случае, если точки А, В и Q (рис.2.24) лежат на одной прямой?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.8.247 (0.125 с.) |


 и
и 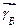 . Тогда, в соответствии с правилом сложения векторов,:
. Тогда, в соответствии с правилом сложения векторов,: .
.
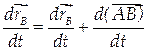 .
. , то выражение переходит в равенство скоростей точек:
, то выражение переходит в равенство скоростей точек: =
=  .
.
 =
=  .
.

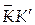 , причем связь длины дуги (криволинейной координаты s) с углом поворота тела определяется выражением:
, причем связь длины дуги (криволинейной координаты s) с углом поворота тела определяется выражением:
 =
= 
 .
.

 .
.


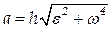 .
.
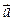 определим по формуле (2.30) с использованием выражений (2.43) и (2.44):
определим по формуле (2.30) с использованием выражений (2.43) и (2.44):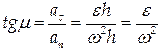 .
.


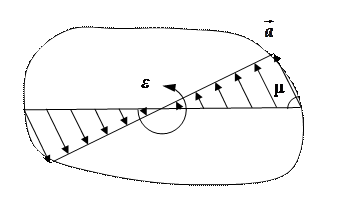

 угловая скорость и угол поворота тела в начальный момент времени, т.е. при
угловая скорость и угол поворота тела в начальный момент времени, т.е. при  .
.
 ).
). постоянно по времени, угловая скорость меняется линейно от времени, а угол поворота – по квадратичному закону. Этот случай движения носит название равнопеременное вращение тела и математически выражается следующими зависимостями:
постоянно по времени, угловая скорость меняется линейно от времени, а угол поворота – по квадратичному закону. Этот случай движения носит название равнопеременное вращение тела и математически выражается следующими зависимостями:
 и углового ускорения
и углового ускорения  тела. Расположение и ориентация векторов будут соответствовать оси вращения тела, т.е. они будут направлены вдоль оси по направлению движения правого винта (если его вращать в сторону действующих угловой скорости ω и углового ускорения ε), а их модули будут равны, соответственно, численным (скалярным) значениям угловой скорости и углового ускорения (рис.2.15).
тела. Расположение и ориентация векторов будут соответствовать оси вращения тела, т.е. они будут направлены вдоль оси по направлению движения правого винта (если его вращать в сторону действующих угловой скорости ω и углового ускорения ε), а их модули будут равны, соответственно, численным (скалярным) значениям угловой скорости и углового ускорения (рис.2.15).

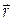 точки К (рис. 2.16).
точки К (рис. 2.16).
 . Модуль вектора равен
. Модуль вектора равен  . Следовательно, вектор, направленный вдоль
. Следовательно, вектор, направленный вдоль  , в соответствии с (2.17), и есть вектор скорости
, в соответствии с (2.17), и есть вектор скорости 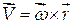 .
.
 .
. слева – вектор
слева – вектор 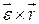 ), так же, как и вектор
), так же, как и вектор  . Вектор, соответствующий второму слагаемому справа (
. Вектор, соответствующий второму слагаемому справа (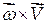 ), направлен по радиусу h к оси вращения (см. «Правило правого винта» и рис. 2.15). Модуль этого вектора равен нормальному (центростремительному) ускорению точки вращающегося тела:
), направлен по радиусу h к оси вращения (см. «Правило правого винта» и рис. 2.15). Модуль этого вектора равен нормальному (центростремительному) ускорению точки вращающегося тела:  . Таким образом, получены формулы для полного, касательного и нормального ускорений в случае задания вращения тела в векторной форме:
. Таким образом, получены формулы для полного, касательного и нормального ускорений в случае задания вращения тела в векторной форме: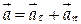 ,
,
 ,
,
 .
.

 отрезка АМ.
отрезка АМ.
 , либо
, либо
 ,
,
 и
и  описывают поступательное движение фигуры S вместе с полюсом А, функция
описывают поступательное движение фигуры S вместе с полюсом А, функция  - вращение фигуры вокруг полюса.
- вращение фигуры вокруг полюса. .
. ,
, ,
,
 – скорость произвольной точки В тела,
– скорость произвольной точки В тела,  – скорость полюса, `
– скорость полюса, `  = ω∙АВ.
= ω∙АВ.

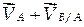 выполнено по правилу треугольника, и рисунок 2.21, где сложение выполнено по правилу параллелограмма.
выполнено по правилу треугольника, и рисунок 2.21, где сложение выполнено по правилу параллелограмма. .
. , откуда
, откуда  . Поскольку VР/А = w×AP и `
. Поскольку VР/А = w×AP и `  перпендикулярен отрезку AP, то мгновенный центр скоростей (м.ц.с.) будет находиться на перпендикуляре к
перпендикулярен отрезку AP, то мгновенный центр скоростей (м.ц.с.) будет находиться на перпендикуляре к  .
.
 . Поскольку VP = 0, то окончательно:
. Поскольку VP = 0, то окончательно:  , а ее модуль равен:
, а ее модуль равен: .
.
 .
.



 =
= 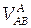 , или
, или  .
.
 .
.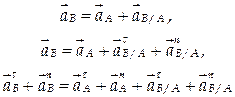
 ) произвольной точки В тела при плоскопараллельном движении равен геометрической сумме векторов ускорения полюса (
) произвольной точки В тела при плоскопараллельном движении равен геометрической сумме векторов ускорения полюса ( ) и полного ускорения (
) и полного ускорения (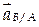 ) точки при ее вращении относительно полюса.
) точки при ее вращении относительно полюса. различаются, поскольку траектории движения точек А и В вообще говоря разные, а траектория движения т. В относительно т. А – окружность радиуса АВ. Поэтому нормальный вектор
различаются, поскольку траектории движения точек А и В вообще говоря разные, а траектория движения т. В относительно т. А – окружность радиуса АВ. Поэтому нормальный вектор  направлен из т. В в т. А вдоль ВА, а касательный вектор
направлен из т. В в т. А вдоль ВА, а касательный вектор  перпендикулярен АВ и направлен в сторону углового ускорения тела.
перпендикулярен АВ и направлен в сторону углового ускорения тела.
 которой в данный момент времени равна нулю (
которой в данный момент времени равна нулю ( ).
). .
.




