
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение твердого тела вокруг неподвижной точки.
Закон сферического движения
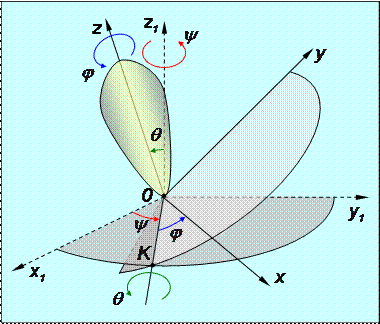
Рис.2.25 Скрепленная, связанная с этим телом координатная система Oxyz поворачиваясь вместе с ним, образует три ориентационных угла φ, ψ, θ, характеризующих положение тела относительно неподвижной системы координат Ox1y1z1. Эти углы, введенные Эйлером, носят названия угол собственного вращения φ, угол прецессии ψ и угол нутации θ. Названия углов соответствуют принятым в небесной механике. Рассмотрим их определение подробнее (рис. 2.25). · Назовем прямую ОК пересечения плоскостей Ox1y1 и Oxy линией узлов. Как следует из ее определения, она перпендикулярна осям Oz1 и Oz. · Угол собственного вращения φ связан с поворотом тела вокруг собственной оси вращения Oz (для волчка – поворот вокруг своей оси). · Угол нутации θ определяет отклонение оси собственного вращения Oz от направления неподвижной оси Oz1 (отклонение оси волчка от вертикали). · Угол прецессии ψ - это угол между линией узлов и неподвижной осью Ox1, или, что одно и то же, угол поворота плоскости осей Oz1z вокруг оси Oz1 (угол поворота оси волчка вокруг вертикальной оси). Заметим, что показанные на рис.2.25 направления углов соответствуют положительным направлениям, принятым в системах координат с правыми тройками направляющих ортов осей. Закон сферического движения абсолютно твердого тела, описывающего его положение в любой момент времени, можно сформулировать в виде:
Угловая скорость при сферическом движении Продифференцировав выражения (2.61) по времени, можно найти угловые скорости вращений по соответствующим осям
Таким образом, движение тела можно представить, как последовательность элементарных поворотов на угол Спроецируем равенство (2.62) на связанные с телом оси x, y, z и учтя, что
(следует из рис. 2.25), получим:
Действуя аналогично при проецировании вектора
Выражения (2.63) и (2.64) получили названия кинематические уравнения Эйлера. Они определяют проекции вектора мгновенной угловой скорости на подвижные и неподвижные оси. Угловое ускорение при сферическом движении В соответствии с определением, угловое ускорение тела есть производная по времени от вектора угловой скорости:
Проекции углового ускорения на неподвижные оси считаются, как производные по времени от соответствующих компонент угловой скорости:
Таким образом, вектора Скорости точек тела при сферическом движении Для определения скоростей точек тела при сферическом движениивоспользуемся формулой (2.51) для вращения с мгновенной угловой скоростью
Таким образом, раскрывая определитель, можно получить выражения для компонентов вектора скорости в связанных с телом координатах точки при его сферическом движении:
В используемых здесь координатах, скрепленных с телом, x, y, и z для конкретной точки есть величины постоянные (в отличие от меняющихся координат x1, y1, и z1 точки в неподвижной системе).
Ускорения точек тела при сферическом движении Для определения ускорений точек тела при сферическом движениивоспользуемся формулой (2.52):
Компоненты вектора полного ускорения, первое ускорение
На этом краткий анализ сферического движения закончим.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое сферическое движение абсолютно твердого тела? Каким законом движения оно характеризуется? 2. Как определяются угловые скорости и ускорения тела с неподвижной точкой при его движении? 3. Какими формулами определяются вектора скорости и ускорения точек твердого тела при его сферическом движении?
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.101.95 (0.011 с.) |
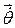
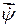
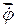
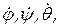 вектора которых направлены вдоль соответствующих осей Oz, Oz1,ОК (рис. 2.25). Их геометрическая сумма представляет собой т.н. «мгновенную угловую скорость тела», меняющуюся с течением времени по величине и направлению:
вектора которых направлены вдоль соответствующих осей Oz, Oz1,ОК (рис. 2.25). Их геометрическая сумма представляет собой т.н. «мгновенную угловую скорость тела», меняющуюся с течением времени по величине и направлению: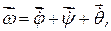
 , совершаемых вокруг перемещающейся в пространстве мгновенной оси вращения
, совершаемых вокруг перемещающейся в пространстве мгновенной оси вращения 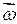 . Следует заметить, что мгновенная ось вращения при любых положениях тела всегда проходит через неподвижную точку О.
. Следует заметить, что мгновенная ось вращения при любых положениях тела всегда проходит через неподвижную точку О.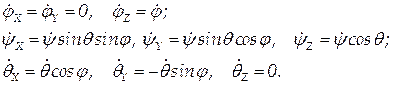

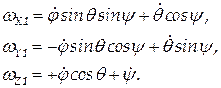
 .
.
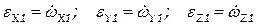 .
.
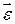 - основные характеристики движения тела с одной неподвижной точкой.
- основные характеристики движения тела с одной неподвижной точкой. .
.
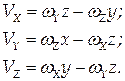
 .
.
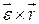 называют вращательным, а второе
называют вращательным, а второе 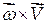 - осестремительным. Заметим, что, при сферическом движении, в отличии от вращения вокруг неподвижной оси, вращательное ускорение вообще говоря не является касательным, а осестремительное – нормальным ускорениями.
- осестремительным. Заметим, что, при сферическом движении, в отличии от вращения вокруг неподвижной оси, вращательное ускорение вообще говоря не является касательным, а осестремительное – нормальным ускорениями.


