
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чисельний аналіз розв’язуючих властивостей неоднорідної імпедансної смугиСодержание книги
Поиск на нашем сайте
4.1 Залежність розв’язуючих властивостей неоднорідної імпедансної смуги від кількості імпедансних смужок, розташованих на ній
В [5] показано, що ширину імпедансної смуги доцільно вибирати не більш за 5λ. Надалі всі розрахунки в дипломній роботі будуть дані для випадку Для оцінки розв’язуючих властивостей імпедансної смуги на величину розв’язки були проведені розрахунки величини При практичній реалізації імпедансної смуги за допомогою ребристої структури її канавки можуть бути розташовані на різній відстані друг від друга і мати різну ширину. У [4] показано, що канавки ребристої структури не впливають одна на одну в тому випадку, коли вони знаходяться друг від друга на відстані не менш 0,1λ. У зв'язку з цим необхідно з'ясувати, як буде мінятися величина 1).Розраховувалася величина 2). Розраховувалася величина 3). Для вище зазначених умов розраховувались модуль, дійсна та мнима частини щільності поверхневого струму на імпедансній смузі. В якості прикладів на рис 4.1 - 4.8 приведені залежності коефіцієнта придушення h та модуля, дійсної та мнимої частини щільності струму
Рисунок 4.1- Залежність коефіцієнта придушення h від кількості імпедансних смужок шириною
Рисунок 4.2- Залежність модуля щільності струму
Рисунок 4.3- Залежність дійсної частини щільності струму
Рисунок 4.4 - Залежність мнимої частини щільності струму

Рисунок 4.5- Залежність коефіцієнта придушення h від кількості імпедансних смужок шириною
Рисунок 4.6- Залежність модуля щільності струму

Рисунок 4.7- Залежність коефіцієнта придушення h від кількості імпедансних смужок шириною
Рисунок 4.8- Залежність модуля щільності струму Таблиця 4.1 - Значення коефіцієнта придушення η для величіні імпедансу
Таблиця 4.2 - Значення коефіцієнта придушення η для величіні імпедансу
Таблиця 4.3 - Значення коефіцієнта придушення η для величіні імпедансу
Із проведених розрахунків можна зробити слідуючи важливі висновки: 1). В області де на імпедансних смужках розподілений ємнісний імпеданс зі збільшенням їх числа на імпедансній смузі значення коефіцієнта придушення збільшуються. При цьому збільшення кількості імпедансних смужок більш ніж вісім не приводить до значного зросту значення коефіцієнта придушення. 2). Коли на імпедансних смужках розподілений ємнісний імпеданс, то зі збільшенням їх ширини 3) Із рисунка 4.2 видно, що осцилюючий характер модуля струму виникає на самих імпедансних смужках. Значення модуля струму при десятьох імпедансних смужках менш ніж при одній, що приводить до збільшення значень коефіцієнта придушення. Також максимальне значення поверхневого струму знаходиться біля джерела магнітного струму. Струм який розповсюджується на імпедансній смузі убуває. 4). Із рисунків 4.3-4.4 видно, що дійсна та мнима частини поверхневого струму мають найбільше значення біля джерела досягають при індуктивному імпедансі 5). Коли на імпедансній смузі розповсюджується поверхнева хвиля мається область, в якій коефіцієнт придушення від’ємний ( 6). Із рисунка 4.6 видно, що осцилюючий характер модуля струму виникає на самих імпедансних смужках, при цьому струм відбивається від країв імпедансних смужок. Значення модуля струму, як і у випадку ємнісного імпедансу при десятьох імпедансних смужках менш ніж при одній, що приводить до збільшення значень коефіцієнта придушення. Також максимальне значення поверхневого струму знаходиться біля джерела магнітного струму. Струм який розповсюджується на імпедансній смузі убуває. 7). Із рисунка 4.7 видно, що в області де на імпедансних смужках розподілений індуктивний імпеданс 8). Із рисунка 4.8 видно, що для імпедансу 9). Із таблиць 4.1-4.3 випливає, що найбільше значення коефіцієнта придушення можна досягти при індуктивному імпедансі, у випадку коли на імпедансній смузі не розповсюджується поверхнева хвиля, при десяти імпедансних смужках та їх ширині Проведені розрахунки показують, що збільшення ширини імпедансних смужок при однаковому їхньому числі, приводить до зменшення величини
4.2 Аналіз діапазонних властивостей неоднорідної імпедансної смуги
При практичній реалізації розв’язуючої плоскої структури необхідно враховувати її діапазонні властивості. Для оцінки діапазонних властивостей розв’язуючої імпедансної смуги розраховувалась величина В якості прикладів на рис 4.9-4.11 приведені залежності коефіцієнта придушення h від
Рисунок 4.9- Залежність коефіцієнта придушення h від довжини хвилі
Рисунок 4.10 - Залежність коефіцієнта придушення h від довжини хвилі
Рисунок 4.11 - Залежність коефіцієнта придушення h від довжини хвилі
Таблиця 4.4 - Значення коефіцієнта придушення η для величіні імпедансу
Із проведених розрахунків можна зробити слідуючи висновки: 1). Коли на імпедансній смузі розташовані смужки з ємнісним імпедансом, то зі збільшенням чи зменшенням довжини хвилі значення коефіцієнта придушення змінюються відповідно. При цьому значення коефіцієнта придушення при десяти смужках приблизно на 10 дБ більш ніж при одній смужці (див. рис. 4.9). 2). Із рисунку 4.10 видно, що характер змінення коефіцієнта придушення для різної кількості імпедансних смужок однаковий. Зі збільшенням кількості імпедансних смужок коефіцієнт придушення значно зменшується. Розв’язуючі властивості імпедансної смуги з однією смужкою зі збільшенням довжини хвилі більш ніж 3). Із рисунку 4.11 видно, що характер змінення коефіцієнта придушення для різної кількості імпедансних смужок однаковий. Зі збільшенням кількості імпедансних смужок коефіцієнт придушення збільшується. 4). В області коли на імпедансній смузі не розповсюджується поверхнева хвиля (див. рис 4.11), як і у випадку імпедансної смуги з однорідним розподілом імпедансу, зі збільшенням довжини хвилі від 3 см до 3,4 см коефіцієнт придушення збільшується. Максимум розв’язки при різній кількості імпедансних смужок досягає при 5). При довжині хвилі 6). Із таблиці 4.4 випливає, що найбільше значення коефіцієнта придушення досягає у випадку, коли довжина хвилі дорівнює Із проведеного аналізу властивостей неоднорідної імпедансної смуги випливає наступне: - найбільше значення коефіцієнта придушення можна досягти при індуктивному імпедансі, у випадку коли на імпедансній смузі не розповсюджується поверхнева хвиля; - найбільше значення коефіцієнта придушення можна досягти у тому випадку, коли імпедансні смужки розташовані безпосередньо біля країв імпедансної смуги; - коли на імпедансних смужках розподілений ємнісний імпеданс, то така розв’язуюча імпедансна смуга є широкополосною; - найбільше значення коефіцієнта придушення можна досягти у тому випадку, коли на імпедансних смужках розподілений індуктивний імпеданс та не розповсюджується поверхнева хвиля при зменшенні довжини хвилі.
ВИСНОВКИ та ПРОПОЗИЦІЇ
В дипломній роботі проведено аналіз розв’язуючих властивостей імпедансної смуги з однорідним та неоднорідним розподіленням імпедансу. Проведені дослідження діапазонних властивостей імпедансної смуги з однорідним та неоднорідним розподіленням імпедансу. Результати роботи такі.
4. Найбільшого значення коефіцієнта придушення можна досягти при неоднорідному індуктивному імпедансі, у випадку коли на імпедансній смузі не розповсюджується поверхнева хвиля. При цьому виявилося, що величина
Отримані в дипломній роботі результати можуть бути використані на практиці при розробці ребристих структур, які використовуються в якості розв’язуючих приладів.
ПЕРЕЛІК ПОСИЛАНЬ 1. Терешин О.Н. Развязка двух антенн щелевого типа, при помощи ребристой структуры, расположенной в плоскости щелей // Радиотехника и электроника. – 1960. - № 12. – С. 1943-1950. 2. Кюркчан А.Г. Связь между антеннами в присутствии ребристых структур // Радиотехника и электроника, АН СССР, 1985. - № 7. – С. 1362. 3. Цалиев Т.А., Черенков В.С. Анализ развязывающих свойств однородной импедансной полосы, расположенной на бесконечном экране // Радиотехника и электроника. – 1983. – № 1. С. 165-167. 4. Черенков В.С., Гладких В.И. Анализ развязывающих свойств ребристой структуры // Наукові праці ОНАЗ ім. О.С. Попова. – 2003. – № 2. – С. 43-48. 5. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. – М.: Радио и связь, 1983. – 376 с. 6. Терешин О.Н., Седов В.М., Чаплин Л.Ф. Синтез антенн на замедляющих структурах. – М.: Связь, 1980. – 135 с. 7. Лошухин Ю.Я., Чимитдоржиев Н.Б. Уменьшение взаимного влияния антенн на неровной проводящей кромке // Тезисы докладов и сообщений Всесоюзного научно-технического симпозиума «Электромагнитная совместимость радиоэлектронных средств». – М.: 1986. С. 57-58. 8. Ямпольский В.Г., Фролов О.П. Антенны и ЭМС. – М.: Радио и связь, 1983. – 272 с. 9. Полищук И.М., Черенков В.С. Об электродинамическом подходе к задаче синтеза антенн с излучающим отверстием в металлической поверхности // Радиотехника и электроника. – 1973. - № 12. – С. 242 250. 10. Полищук И.М., Черенков В.С. Задача дифракционного синтеза антенн с дополнительным условием на уровне поля в зоне тени // Радиотехника и электроника. – 1980. - № 7. – С. 1405-1419. 11. Чаплин А.Ф. О единственности решения уравнений Максвелла в области с импедансными граничными условиями // Известия вузов. Сер. Радиоэлектроника. – 1967. - № 12. – С. 1214-1218. 12. Цалієв Т.А. Електромагнітна сумісність радіоелектронних засобів. Ч.2 Методи забезпечення електромагнітної сумісності радіоелектронних засобів: Конспект лекцій. – Одеса: ОНАЗ, 2003. – 153 с. 13. Чаплин Л.Ф. Возбуждение импедансной полосы на бесконечном экране // Известия вузов. Сер. Радиофизика. – 1963. - № 3. – С. 585-590. 14. Терешин О.Н., Покас Г.И. Синтез пассивных структур, обеспечивающих заданную коррекцию ближних и дальних полей антенны с произвольной поляризацией // Вопросы радиоэлектроники. Сер. Теоретическая радиотехника. – 1975. – Вып. 5. – С. 134-144. 15. Васильев Е.Н. Возбуждение тел вращения. – М.: Радио и связь, 1987. 16. Верлань А.Ф., Сизиков В.С. Интегральные уравнения: методы, алгоритмы, программы. Справочное пособие. – Киев: Наукова Думка. – 1986. – С. 543. 17. Черенков В.С. Рекуррентные формулы в задачах дифракции волн на неоднородной импедансной плоскости // Наукові праці УДАЗ ім. О.С. Попова. – 2000. - №1. – С. 42-46. 18. Гладких В.И. Разработка рекуррентных методов решения задач радиосвязи, моделируемых интегральными уравнениями // Диссертация на соискание научной степени к.т.н. – ОНАС, 2004, 168 листов 19. Справочник по специальным функциям. Под редакцией М. Абрамовица и И. Тигана. – М.: Наука. – 1979. 20. Градштейн И.С., Рыжик И.М. и др. Таблицы интегралов, сумм, рядов и произведений. – М.: Наука. – 1974. 21. ДСТУ 3008 – 95. Документація. Звіти у сфері науки і техніки. Структура і правила оформлення. – К.: Держстандарт України. 1995. – 38 с.
ДОДАТОК А
Рисунок А.1 Функціональна блок-схема загального алгоритму ДОДАТОК Б
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.198 (0.007 с.) |

 .
. для різних значень імпедансу на смузі
для різних значень імпедансу на смузі 
 , друга канавка шириною
, друга канавка шириною  , третя канавка шириною
, третя канавка шириною  . Використовуючи розподіли імпедансу
. Використовуючи розподіли імпедансу  ,
, 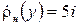 ,
,  , були проведені наступні розрахунки:
, були проведені наступні розрахунки: друг від друга розташовувались від однієї до десяти імпедансних смужок з імпедансом зазначеним вище.
друг від друга розташовувались від однієї до десяти імпедансних смужок з імпедансом зазначеним вище. від кількості імпедансних смужок для різних значень імпедансу.
від кількості імпедансних смужок для різних значень імпедансу.

 (товста лінія),
(товста лінія),  (тонка лінія),
(тонка лінія),  (пунктирна лінія), при
(пунктирна лінія), при 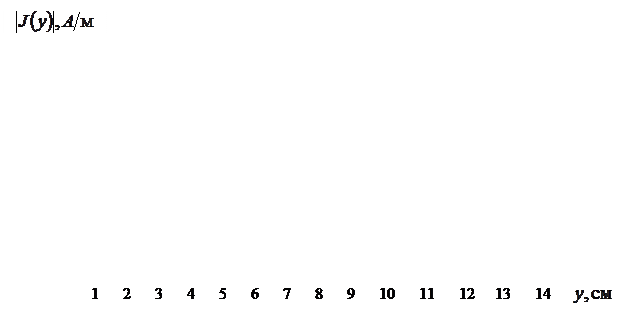

 , коли кількість імпедансних смужок шириною
, коли кількість імпедансних смужок шириною 










 , для випадку
, для випадку 
 , для випадку
, для випадку 
 , для випадку
, для випадку  значення коефіцієнта придушення збільшуються.
значення коефіцієнта придушення збільшуються. . Характер змінення струму на імпедансній смузі при різних імпедансах однаковий.
. Характер змінення струму на імпедансній смузі при різних імпедансах однаковий. ) див. рисунок 4.5. Також є області, в якій коефіцієнт придушення зі збільшенням кількості імпедансних смужок зменшується. Це явище можна пояснити наступним чином. На імпедансній смузі інтерферують дві хвилі – падаюча та відбита. Ці хвилі інтерферують в місцях, де знаходяться імпедансні смужки, при цьому якщо вони протифазні, то коефіцієнт придушення збільшується, якщо вони синфазні, то коефіцієнт придушення зменшується.
) див. рисунок 4.5. Також є області, в якій коефіцієнт придушення зі збільшенням кількості імпедансних смужок зменшується. Це явище можна пояснити наступним чином. На імпедансній смузі інтерферують дві хвилі – падаюча та відбита. Ці хвилі інтерферують в місцях, де знаходяться імпедансні смужки, при цьому якщо вони протифазні, то коефіцієнт придушення збільшується, якщо вони синфазні, то коефіцієнт придушення зменшується. . При цьому виявилося, що величина
. При цьому виявилося, що величина  при
при 








 покращуються. При
покращуються. При 
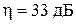 .
. .
. коефіцієнт придушення зменшується незначно.
коефіцієнт придушення зменшується незначно. при різній кількості імпедансних смужок для
при різній кількості імпедансних смужок для  .
.




