
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи оцінки розвязувальних імпедансних структурСодержание книги
Поиск на нашем сайте
2.1 Методи чисельного розв`язання інтегральних рівнянь Фредгольма другого роду.
Апарат інтегральних рівнянь широко застосовується при моделюванні процесів, які застосовуються в багатьох приладах радіозв’язку. Інтегральні рівняння є додатком до задач статистичної динаміки прикладами яких є визначення кореляційної функції стаціонарного випадкового процесу по експериментальним даним і визначення оптимальних динамічних характеристик системи. Важливим достоїнством багатьох чисельних методів, алгоритмів і програм є їх висока універсальність і незалежність від типів розв'язання рівнянь. Існує декілька класів методів розв'язання інтегральних рівнянь: проекційні, інтерполяційні, ітераційні та рекурентні [15-17]. Розглянемо один з найпоширеніших методів розв'язання інтегральних рівнянь другого роду – метод Крилова-Боголюбова, що належить до інтерполяційних методів, а також метод, який оснований на рекурентних формулах. 2.1.1 Метод Крилова-Боголюбова Нехай є ідеально провідна площина, яка збіжна з площиною XOY декартової системи координат. Розташуємо на площині двомірну імпедансну смугу шириною d так, як це показано на рисунку 2.1.На смузі шириною d задано сторонній імпеданс
Рисунок 2.1-Геометрия задачі
Нехай імпеданс Координату середини кожного відрізку позначимо через
Нехай функція розподілення імпедансу представлена кусочно – постійною функцією виду:
де
Звідси походить, що
Підставимо подання (2.2) у рівняння (1.13), тоді це рівняння можна записати у наступному вигляді:
Змінимо місцями додавання та інтегрування у рівнянні (2.4), тоді одержімо
Нехай відрізки шириною Δ настільки малі, що величину
Так як функція
Введемо наступне позначення:
Використаємо (2.8) та перепишемо вираз (2.7), отримаємо:
Подамо в рівнянні (2.9)
де
Співвідношення (2.10) є СЛАР, яку отримано методом Крилова-Боголюбова. Як видно з наведених формул, в цьому методі застосовується кусочно-постійна апроксимація функцій Як визначається в [6,11,16] точність розв’язання інтегральних рівнянь методом Крилова-Боголюбова визначається довжиною інтервалу Δ, яка в свою чергу, визначається в основному, швидкістю змінення ядра рівняння. При цьому, з одного боку, зменшення довжини інтервалу приводить до більш точної апроксимації інтегрального рівняння (1.13) системою (2.10), а з іншого, зменшення довжини інтервалу може привести до росту похибок обчислювання СЛАР (2.10). Звідси походить,що при використанні метода Крилова-Боголюбова необхідно визначати оптимальну кількість розбиття проміжку інтегрування [0,Т] у рівнянні (1.13).
2.1.2 Рекурентні формули чисельного розв'язання інтегральних рівнянь Фредгольма другого роду.
Розглянемо рекурентні формули розв'язання інтегрального рівняння (1.13) як запропоновано у роботі [17]. Розіб’ємо відрізок [0,Т] в рівнянні (1.13) на N елементарних інтервалів шириною Δ. Тоді рівняння (1.13) можна записати у наступному вигляді:
Розглянемо наступне рівняння:
де m може приймати значення 0,1,2,..... N. Очевидно, що при m = N рівняння (2.12) збігається з рівнянням (2.11), а звідси і з рівнянням (1.13). Подамо функцію
де
N – число елементарних інтервалів, на які розбито проміжок інтегрування [0,Т] в рівнянні (1.13).
Подамо в формулі (2.13)
Формула (2.13) зв’язує розв’язок рівняння (2.12) та рівняння (2.14). Іншими словами, формула (2.13) зв’язує розв’язок рівняння (1.13) при різному розподіленні на проміжку [0,Т]. Саме розподілення імпедансу для рівнянь відрізняється на одному елементарному інтервалі. В формулу (2.13) входять функції
де Для функції
Таким чином
З формул (2.13) та (2.16) видно що
Формули (2.13) та (2.16) дозволяють за вихідними функціями Ці формули є одночленними рекурентними формулами, які пов’язують розв’язання рівняння(1.13) при різному розподіленні імпедансу, яке відрізняється на сусідніх елементарних інтервалах. З формул (2.13) та (2.16) походить, що при їх чисельному застосуванні значення функції Відзначимо, точність розв’язання рівняння (1.13) за допомогою рекурентних формул визначається кількістю інтервалів розбиття проміжку [0,Т] N. Саме,чим більше N, тим з більшою точністю формула (2.13) визначає розв’язання рівняння (1.13). Це показано в роботі [18]. Відносна похибка наближеного розв’язання інтегральних рівнянь отриманих при використанні рекурентного методу та зведення рівнянь до СЛАР (метод Крилова-Боголюбова), однакова [18]. Найбільшою перевагою рекурентного методу є те, що рекурентні формули дозволяють визначити явні вирази для величини імпедансу та місцезнаходження канавок на імпедансної смузі.
2.2. Коефіцієнт придушення імпедансної смуги. Як відзначено в [19], прийомну антену можна охарактеризувати величиною стороннього імпедансу, що дорівнює відношенню дотичних складових векторів електричного і магнітного полючи в апертурі антени. У загальному випадку розподіл імпедансу по апертурі буде різним для різних типів антен. Для антен апертурного типу розподіл імпедансу в першому наближенні постійний і дорівнює хвильовому опору вільного простору. Одним з можливих методів проведення оцінки розв'язуючих властивостей імпедансної смуги є метод, при якому визначається відношення потужності, виділюваною прийомною антеною, коли на импедансной смузі розподілений деякий імпеданс до потужності, виділюваною прийомною антеною, коли на імпедансній смузі імпеданс дорівнює нулю. Недоліком такої оцінки є те, що в цьому випадку необхідно знати тип приймальної антени. Цей метод був використаний у роботах [19,20]. У [19] проводилась оцінка властивостей ребристої розв'язуючий структури шляхом визначення коефіцієнта придушення. Цей коефіцієнт визначається наступною формулою:
де З формули (2.18) видно, що коефіцієнт придушення h визначається відношенням норми щільності струму на відрізку Як уже відзначалося, недоліком коефіцієнта (2.18) є необхідність знання розподілу імпедансу приймальної антени. Відзначимо, що в роботі [19] розподіл імпедансу по апертурі приймальної антени було обрано рівним 120p тобто хвильовому опору вакууму. Проаналізуємо поводження коефіцієнта придушення h, що характеризує розв'язуючі властивості смуги
2.3. Про оцінку впливу приймальної антени на розв'язуючі властивості імпедансної смуги. Власний коефіцієнт придушення імпедансної смуги.
Для визначення оцінки впливу приймальної антени на розв'язуючі властивості імпедансної смуги були проведені розрахунки струму на смузі Розрахунки проводилися для різних моделей приймальної антени, для різних значень ширини імпедансної смуги з однорідним розподілом імпедансу. При цьому ширина Приклади розрахунків (для двох моделей приймальної антени) представлені на рисунках 2.2-2.5. Для першої моделі покладалося, що нормований імпеданс приймальної антени в області d дорівнює одиниці (

Рисунок 2.2 - Розподіл модулів струму (
Рисунок 2.3 - Розподіл модулів струму (
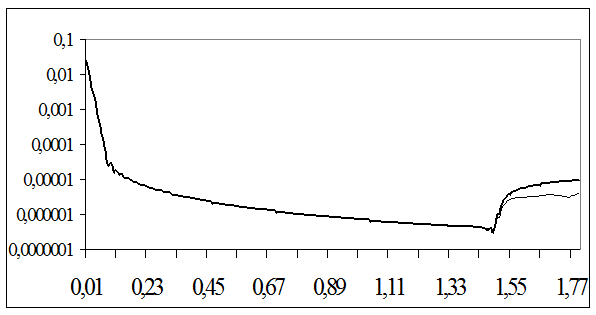
Рисунок 2.4 - Розподіл модулів струму (
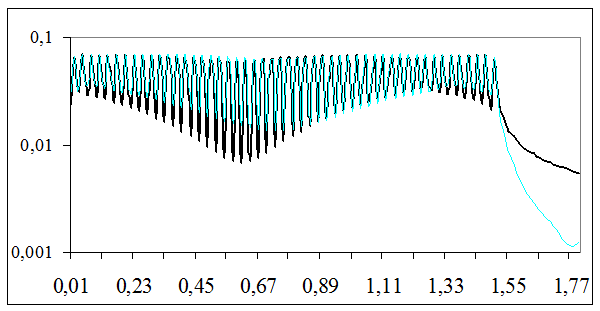
На рисунках 2.2–2.5 тонка лінія відповідає першої моделі ( Аналіз чисельних результатів для модулів струму дозволяє зробити наступні висновки: 1. На смузі d (місце розташування приймальної антени) норма струму при 2. Розподіл модуля струму на однорідній імпедансній смузі залежить тільки від величини її імпедансу і не залежить від імпедансу приймальної антени. 3. Якщо імпеданс має ємнісний характер, то модуль струму має максимальне значення біля краю смуги, розташованого поблизу стороннього джерела струму (див. рис. 2.2). Це підтверджує той факт, що ємнісний імпеданс «віджимає» електромагнітне поле від імпедансної поверхні. Характер розподілу модуля струму при однорідному ємнісному імпедансі на імпедансної смузі не міняється при зміні її ширини. 4. Мається область зміни величини однорідного індуктивного імпедансу (при l=3 см, 0£ Осцилірующий розподіл струму можна пояснити в такий спосіб. Уздовж імпедансної смуги поширюються дві поверхневі хвилі (пряма і відбита). Ці хвилі інтерферують одна з одною. При цьому Розрахунки “коефіцієнта бігучої хвилі,” (КБХ) на імпеданснії смузі показали, що КБХ у випадку 5. Якщо імпеданс має індуктивний характер і такий, що не належить області, відзначеної в попередньому пункті, тобто 6. У випадку розповсюдження поверхневої хвилі характер розподілу модуля струму в області приймальної антени відрізняється від випадку, коли поверхнева хвиля на смузі Перейдемо до аналізу коефіцієнта придушення імпедансної смуги h, визначеного формулою (2.18). На рис. 2.5 в якості прикладу приведені залежності коефіцієнта придушення (величина h) від величини індуктивного імпедансу На цьому рисунку тонка лінія відповідає
Рисунок 2.5 - Залежність коефіцієнта придушення від величини індуктивного імпедансу для двох моделей приймальної антени
Розрахунки коефіцієнта придушення дозволяють відзначити наступне: · коефіцієнт придушення (див. рис. 2.5, а також рис. 2.6, що приведений нижче) істотно міняється при зміні · коефіцієнт придушення h для · при зміні довжини імпедансної смуги характер зміни коефіцієнта придушення не змінюється. Проведені розрахунки говорять про те, що коефіцієнт придушення, обумовлений формулою (2.18), зручно використовувати в тому випадку, коли відома величина імпедансу приймальної антени, апертура якої розташовується в області d. У цьому випадку коефіцієнт h характеризує зменшення потужності на вході приймальної антени за рахунок використання імпедансної смуги. Коли величина стороннього імпедансу приймальної антени невідома, використання формули (2.18) не завжди дозволяє правильно оцінити вплив імпедансної смуги. У цьому випадку як оцінку розв'язуючих властивостей імпедансної смуги використовується величина
Відзначимо, що струм на імпедансної смузі практично не міняється при зміні імпедансу приймальної антени. З порівняння формул (2.18) і (2.19) видно, що для визначення h необхідно знати властивості приймальної антени. Для визначення величини За допомогою формул (2.18) і (2.19) були проведені чисельні розрахунки величин h і При розрахунку величини h імпеданс на відрізку Проведені розрахунки показують, що характер зміни величин h і При реалізації системи реальні величини розв'язки завжди будуть більше розрахованих величин.
Рисунок 2.6 - Залежність h і
Як показано в [21] величину доцільно використовувати при розгляді задачі порушення неоднорідної імпедансної смуги За допомогою рекурентних формул можна отримати нові формулі для вирішення задачі синтезу розв’язуючої імпедансної смуги, яка реалізована в вигляді ребристої структури. Ці формули у явному вигляді дозволяють знайти імпеданс та місце розташування канавок на ребристій структурі. При цьому мінімум норми комплексної амплітуди току шукається в області апертури приймальної антени. У зв’язку с цим у розділах 3 та 4 дипломної роботи буде розглядатись коефіцієнт придушення, який визначається формулою (2.18).
|
|||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.242.223 (0.008 с.) |

 . Нехай зліва від імпедансної смузі (при
. Нехай зліва від імпедансної смузі (при  ) розташована нитка стороннього (збуджуючого площину) магнітного струму одиничної амплітуди, а справа від смуги знаходиться область шириною
) розташована нитка стороннього (збуджуючого площину) магнітного струму одиничної амплітуди, а справа від смуги знаходиться область шириною 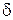 , в межах якої задано значення імпедансу
, в межах якої задано значення імпедансу 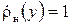 , де розташована апертура приймальної антени.
, де розташована апертура приймальної антени.
 , не дорівнює нулю на кінцевому відрізку [0,Т]. Розіб’ємо цей відрізок на N елементарних відрізків однакової довжини Δ.
, не дорівнює нулю на кінцевому відрізку [0,Т]. Розіб’ємо цей відрізок на N елементарних відрізків однакової довжини Δ. , яка визначається наступним виразом:
, яка визначається наступним виразом: . (2.1)
. (2.1)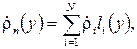 (2.2)
(2.2) , i = 1,2,….., N- 1.
, i = 1,2,….., N- 1. . (2.3)
. (2.3) . (2.4)
. (2.4) . (2.5)
. (2.5) на них можна вважати постійною. Позначимо значення щільності струму в середині кожного відрізку Δ через
на них можна вважати постійною. Позначимо значення щільності струму в середині кожного відрізку Δ через  . В цьому випадку рівняння (2.5) можна записати в наступному вигляді:
. В цьому випадку рівняння (2.5) можна записати в наступному вигляді: . (2.6)
. (2.6) дорівнює одиниці на проміжку
дорівнює одиниці на проміжку  , а поза ним дорівнює нулю, то останнє рівняння набуває вигляду
, а поза ним дорівнює нулю, то останнє рівняння набуває вигляду . (2.7)
. (2.7) . (2.8)
. (2.8) . (2.9)
. (2.9) , тоді отримаємо систему лінійних алгебраїчних рівнянь (СЛАР) наступного вигляду:
, тоді отримаємо систему лінійних алгебраїчних рівнянь (СЛАР) наступного вигляду: (2.10)
(2.10)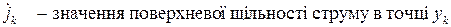 ;
; ;
; .
. ,
,  та функції правої частини. Ці функції визначені своїми значеннями в точках
та функції правої частини. Ці функції визначені своїми значеннями в точках  , які є серединами елементарних інтервалів та на які розбито проміжок інтегрування [0,Т] в рівнянні (1.13).
, які є серединами елементарних інтервалів та на які розбито проміжок інтегрування [0,Т] в рівнянні (1.13).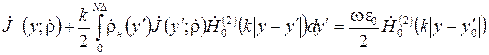 . (2.11)
. (2.11) . (2.12)
. (2.12) (2.13)
(2.13)
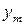 - середина m –го елементарного інтервалу Δ;
- середина m –го елементарного інтервалу Δ;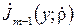 - функція, яка є розв’язком рівняння виду:
- функція, яка є розв’язком рівняння виду: . (2.14)
. (2.14) отримаємо:
отримаємо:
 . Ці функції є розв’язанням наступного інтегрального рівняння:
. Ці функції є розв’язанням наступного інтегрального рівняння: , (2.15)
, (2.15)
 визначається формулою (2.8).
визначається формулою (2.8). (2.16)
(2.16)

 , (2.17)
, (2.17) .
. та
та  обчислити функції
обчислити функції  ,
, 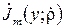 та
та  (2.18)
(2.18) ;
;  - нормовані сторонні імпеданси смуг
- нормовані сторонні імпеданси смуг  і d (див. рисунок 2.1);
і d (див. рисунок 2.1);  - значення імпедансу у відповідних смугах;
- значення імпедансу у відповідних смугах;  - комплексна амплітуда щільності електричного струму на смузі d, на якій розташована апертура прийомної антени, що залежить від величини стороннього імпедансу
- комплексна амплітуда щільності електричного струму на смузі d, на якій розташована апертура прийомної антени, що залежить від величини стороннього імпедансу  ;
;  - комплексна амплітуда щільності електричного струму на смузі d при
- комплексна амплітуда щільності електричного струму на смузі d при  = 0;
= 0;  ,
,  - абсолютні діелектрична і магнітна проникності верхнього півпростору.
- абсолютні діелектрична і магнітна проникності верхнього півпростору. у випадку, коли імпеданс на смузі
у випадку, коли імпеданс на смузі  і коефіцієнта придушення, визначеного формулою (2.18).
і коефіцієнта придушення, визначеного формулою (2.18).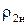 = 1), що відповідає імпедансу 120p, розподіленому в апертурі приймальної антени. Для другої моделі покладалося, що нормований імпеданс приймальної антени в області d дорівнює нулю (
= 1), що відповідає імпедансу 120p, розподіленому в апертурі приймальної антени. Для другої моделі покладалося, що нормований імпеданс приймальної антени в області d дорівнює нулю (
 ,
, 
 ,
, 
 ,
,  =0). На рисунках 2.2-2.4 представлені розподіли модулів струму на відрізку [0,
=0). На рисунках 2.2-2.4 представлені розподіли модулів струму на відрізку [0,  завжди більше, ніж при інших розподілах імпедансів
завжди більше, ніж при інших розподілах імпедансів 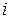 12,8), коли струм на імпедансній смузі осцилює. Розміри цієї області збільшуються з ростом довжини хвилі. При цьому число осциляцій струму залежить від величини імпедансу.
12,8), коли струм на імпедансній смузі осцилює. Розміри цієї області збільшуються з ростом довжини хвилі. При цьому число осциляцій струму залежить від величини імпедансу. поверхневої хвилі залежить від величини імпедансу, що і можна було очікувати.
поверхневої хвилі залежить від величини імпедансу, що і можна було очікувати. =0 завжди менше, ніж для інших моделей приймальної антени, що не суперечить відомим представленням [22].
=0 завжди менше, ніж для інших моделей приймальної антени, що не суперечить відомим представленням [22]. ³
³ 
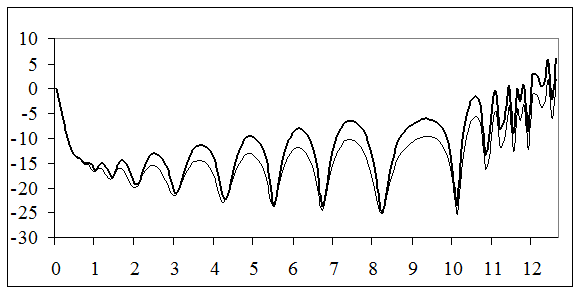
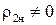 , крім випадку, коли величина
, крім випадку, коли величина  , що визначається за наступною формулою [5]:
, що визначається за наступною формулою [5]: (2.19)
(2.19) (
(





