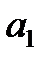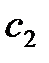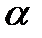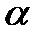Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перечень практических заданий для проведения зачетаСодержание книги
Поиск на нашем сайте
по дисциплине «Линейная алгебра» Контрольная работа №1 Задача 1. Даны матрицы:
1. Вычислить матрицу 2. Проверить выполнение равенства 3. Вычислить определители
4. Решить систему уравнений 5. Решить систему уравнений
Таблица данных по вариантам к задаче 1
Задача 2. 1. Даны векторы 2. Найти линейную комбинацию векторов 3. Будут ли векторы линейно зависимы или линейно независимы в случаях: а) в)
Задача 3. Даны три вектора Задача 4. 1. Даны векторы
2. Вычислить площадь и высоту треугольника 3. Вершины треугольной пирамиды находятся в точках
Задача 5. Даны две точки а) проходящей через точку б) проходящей через две точки
Задача 6. Даны три точки а) проходящей через точку б) проходящей через три точки
в) проходящей через прямую г) проходящей перпендикулярно плоскости
Задача 7. Найти точку пересечения плоскости
Задача 8. В треугольнике а) уравнение прямой б) уравнение высоты в) уравнение медианы
Задача 9. Построить кривые по их уравнениям и определить их тип: а) в) д) Таблица данных по вариантам к задачам 2-9
Вопросы к экзамену 1. Понятие матрицы и ее размерности. Линейные операции над матрицами. Умножение матриц. 2. Понятие определителя второго порядка. Правило треугольников вычисления определителей третьего порядка. 3. Понятие и свойства определителей произвольного порядка. 4. Минор и алгебраическое дополнение элемента определителя. Универсальное правило вычисления определителей. 5. Обратная матрица; 6. Ранг матрицы; 7. Система линейных уравнений; 8. Теорема Кронекера-Каппелли; 9. Формулы Крамера; 10. Матричный метод; 11. Метод Гаусса; 12. Метод Жордана Гаусса; 13. Определение вектора; 14. Линейные действия над векторами; 15. Базис. Линейная независимость векторов; 16. Определение скалярного произведения и его свойства; 17. Выражение скалярного произведения в координатах; 18. Правые и левые тройки векторов; 19. Определение и свойство векторного и смешанного произведений; 20. Понятие линейного оператора и его матрицы. 21. Собственные числа и векторы линейного операторы, методика их нахождения.
22. Общее уравнение прямой; 23. Каноническое уравнение прямой; 24. Параметрические уравнения прямой; 25. Уравнение прямой с угловым коэффициентом; 26. Условия пересечения, коллинеарности и ортогональности двух прямых заданных общими уравнениями; 27. Условия пересечения, коллинеарности и ортогональности двух прямых заданных уравнениями других форм; 28. Нормированное уравнение прямой. Расстояние от точки до прямой; 29. Общее уравнение плоскости; 30. Взаимное расположение двух плоскостей в пространстве; 31. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой; 32. Нормированное уравнение плоскости. Расстояние точки от плоскости; 33. Каноническое уравнение прямой в пространстве; 34. Параметрическое уравнение прямой в пространстве; 35. Взаимное расположение двух прямых линий в пространстве; 36. Взаимное расположение прямой и плоскости в пространстве; 37. Поверхности второго порядка. Простейшие уравнения сферы и эллипсоида. Параболоид вращения.
Основная литература: 1. М.С. Красс, Б.П. Чупрынов. Математика для экономистов. Спб.: Питер. 2007. 2. В.А. Ильин, А.В. Куркина. Высшая математика. М.: МГУ, Проспект. 2004. 3. Н.Ш. Кремер. Высшая математика для экономистов. Практикум. М.: ЮНИТИ. 2007. Дополнительная литература: 1. В.И. Ермакова, Справочник по математике для экономистов. 2. Д. Письменный. Конспект лекций по высшей математике. Тридцать пять лекций. М.: Айрис Пресс. 2008.
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ВОПРОСОВ ПО ДИСЦИПЛИНЕ «ФИЗКУЛЬТУРА» 1. Физическая культура в общекультурной и профессиональной подготовке студентов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.46.68 (0.008 с.) |

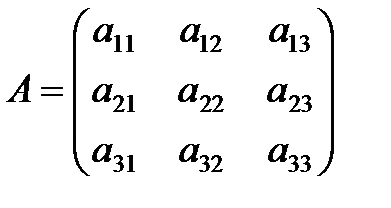 ;
;  ;
; 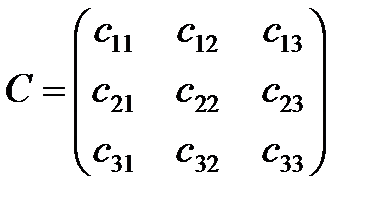 .
. .
. .
.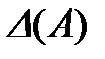 ,
,  ,
, 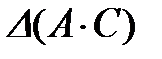 и проверить равенство
и проверить равенство .
.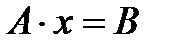 методом Крамера.
методом Крамера. матричным методом.
матричным методом.



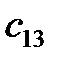



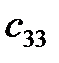

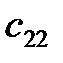


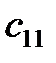


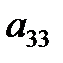



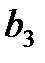
 ,
,  своими декартовыми координатами. Вычислить и изобразить в системе координат следующие линейные комбинации векторов
своими декартовыми координатами. Вычислить и изобразить в системе координат следующие линейные комбинации векторов  и
и  :
:  ,
,  ,
, 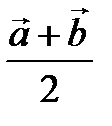 .
. ,
,  и
и 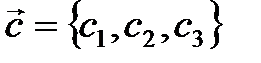 с коэффициентами
с коэффициентами  ,
,  и
и  .
. ) образует базис в пространстве
) образует базис в пространстве  . Найти разложение вектора
. Найти разложение вектора  по этому базису.
по этому базису. , угол между векторами
, угол между векторами и
и  , проекцию вектора
, проекцию вектора 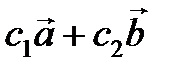 на вектор
на вектор  .
. с вершинами
с вершинами  ,
,  и
и 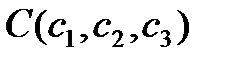 .
. . Вычислить: а) объем пирамиды; б) высоту, опущенную из вершины
. Вычислить: а) объем пирамиды; б) высоту, опущенную из вершины  на основание пирамиды
на основание пирамиды  .
. параллельно вектору
параллельно вектору  ;
; .
.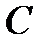 ;
; и точку в пространстве
и точку в пространстве  через точку
через точку  .
. ,
,  и
и  . Составить:
. Составить: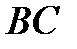 ;
; .
. ; б)
; б) 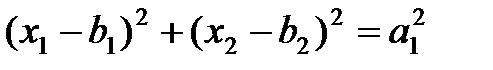 ;
; ; г)
; г)  ;
; ; е)
; е)  .
.