
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет координат батиграфических кривых водохранилища.Содержание книги Поиск на нашем сайте Таблица 1
В графы 1 и 2 вписываем отметки уровня воды и соответствующие им площади водной поверхности водохранилища из исходных данных. Частичные объемы начиная с уровня воды 100 м можно рассчитывать по упрощенной формуле ΔVi=[(Ωi+Ωi+1)/2]*ΔHi, а с 90 м до 100 м каждая последующая площадь превышает предыдущую больше чем в 1,5 раза.. Следовательно, используем формулу ΔVi=1/3(Ωi+ Ωi+1+√ΩiΩi+1)ΔHi. Величины по средней площади вносим в графу 3, принимая, что водная поверхность водохранилища горизонтальная. Первоначальный придонный объем воды в водохранилище (графа 5) определяем по формуле ΔVi=2/3* Ωi*ΔHi, одно последующее значение – по зависимости ΔVi=1/3(Ωi+ Ωi+1+√ΩiΩi+1)* ΔHi, а остальные – по упрощенной формуле ΔVi=[(Ωi+Ωi+1)/2]*ΔHi. В графе 6 последовательно суммируем частичные объемы по формуле VH=Σ ΔVi начиная ото дна. Площадь литорали (графа 7) определяем по формуле ΩLi= ΩHi- ΩHi-2, а критерий литорали (графа 8) – по зависимости LΩi=ΩLi/ ΩHi. Средние глубины воды в водохранилище hср (графа 10) при соответствующих отметках уровня воды в нем рассчитываем по формуле
По данным таблицы строим батиграфические кривые. Построения кривых принимаем таким, чтобы кривые не пересекались, а линии, соединяющие концы кривых V=V(H), Ω=Ω(H), LΩ= LΩ(H) и
Определение нормы годового стока при наличии данных гидрометрических условий. Условия задания. Построить эмпирическую кривую обеспеченности для реки Талой для средних годовых расходов с 1940 по 1956 гг. Найти аналитическую кривую по ординатам трехпараметрического гамма-распределения, оценить достоверность этих кривых по критериям наибольшего правдоподобия. Исходные данные: Таблица 2.
Вычисление параметров эмпирической кривой обеспеченности среднегодовых расходов воды р. Талой за 1940…1956гг. Таблица 3.
При n˂30 квадрат среднеквадратических отклонений равен:
Отсюда найдем дисперсию: По правилу «трех сигм» разброс случайных величин от среднего значения не должен превышать
В данном случае ряд гидрологических наблюдений находится в допустимом интервале. Вычисляем коэффициент вариации (изменчивости) Cυ и коэффициент асимметрии Cs для этого ряда:
9 столбец – процентная обеспеченность по Хазену
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

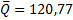
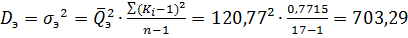 (
(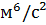 )
)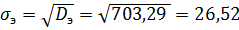 (м³/с).
(м³/с).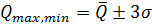 (при α=0,01):
(при α=0,01):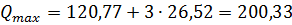 (м³/с),
(м³/с),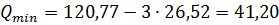 (м³/с).
(м³/с).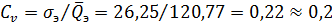 .
.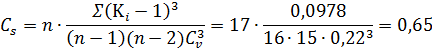
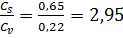 →
→ 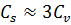 .
.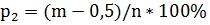 (при
(при 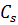 ˃2
˃2 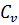 ).
).


