
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формы аналитического описания сигналов
Возможна форма представления сигналов с помощью спектров. Сигнал x () рассматривается как совокупность элементарных сигналов (), умноженных на коэффициенты c и составляющих систему функций { ()} определенного типа: При этом система функций { ()} называется базисной, а представление сигнала в виде (3.1) - его разложением по системе базисных функций или обобщенным рядом (многочленом). Если сигнал x () является комплексным, то и коэффициенты c и система базисных функций { ()} также будут являться комплексными. Если система функций выбрана, то сигнал полностью характеризуется набором (вектором) спектральных коэффициентов { c } - его спектром. В общем случае ряд (3.1) для непрерывных сигналов содержит бесконечное число членов. При практических расчетах такой ряд обычно ограничивают (усекают). В этом случае представление сигнала будет приближенным При этом необходимо сформулировать критерий приближения. 1. Можно потребовать, чтобы максимальное значение погрешности аппроксимации 2. В качестве критерия приближения можно выбрать среднюю погрешность
3. Если в качестве меры представления принимается минимум среднеквадратичной погрешности Все рассмотренные критерии приближения взаимосвязаны. Если ряд (3.2) сходится к x () равномерно, то он тем более сходится среднеквадратически. Из среднеквадратической сходимости вытекает сходимость в среднем. Для того, чтобы разложение сигнала в форме (3.1) было возможным, система базисных функций (СБФ) должна удовлетворять ряду требований: 1) Быть упорядоченной системой линейно независимых функций. 2) Быть полной, для того, чтобы по выбранной системе функций можно было разложить любой сигнал из заданного множества. 3) Число линейно независимых функций в полной системе должно быть равным размерности рассматриваемого множества сигналов, т.е. количеству чисел, с помощью которых можно выбрать любой сигнал из этого множества.
Наиболее удобно если базисная система ортогональна. При представлении сигналов в форме (3.2) необходимо определить способ вычисления спектральных коэффициентов. Он во многом будет зависеть от используемого метода аппроксимации (вида принятого критерия сходимости). В случае применения среднеквадратического критерия коэффициенты c, выбирают таким образом, чтобы среднеквадратическая ошибка s была минимальной. Это достигается с помощью обобщенной формулы Фурье расчета спектра: Увеличивая неограниченно число членов в аппроксимирующем многочлене с коэффициентами в форме (3.10), получим в пределе равенство В спектральном представлении (3.1) и в формуле расчета спектра (3.10) базисные функции являются функциями двух переменных и , а спектральные коэффициенты - функциями переменной . Это приводит к симметрии выражений (3.1) и (3.10), называемых соответственно прямым и обратным преобразованием Фурье, из которой следует математическое равноправие функций
Формулы (3.12) и (3.16) представляют собой дискретные преобразования Фурье.
|
|||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.56 (0.007 с.) |
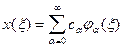 . (3.1)
. (3.1)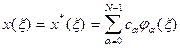 (3.2) и имеет место аппроксимация сигнала x () конечным рядом (3.2).
(3.2) и имеет место аппроксимация сигнала x () конечным рядом (3.2).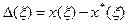 было минимальным на заданном интервале определения функции x (). Этот вид аппроксимации, при котором минимизируется величина
было минимальным на заданном интервале определения функции x (). Этот вид аппроксимации, при котором минимизируется величина 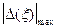 , называется равномерным приближением.
, называется равномерным приближением.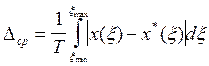 , где T = max - min. Такая аппроксимация называется приближением в среднем.
, где T = max - min. Такая аппроксимация называется приближением в среднем.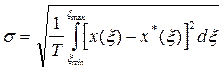 , то такой вид аппроксимации называется приближением в среднеквадратическом.
, то такой вид аппроксимации называется приближением в среднеквадратическом.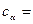 [1/(Q
[1/(Q 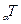 )]·
)]· 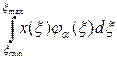 . (3.10)
. (3.10)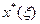 =
= 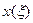 , выполняемое при s. При этом аппроксимирующий многочлен примет вид бесконечного ряда, называемого обобщенным рядом Фурье.
, выполняемое при s. При этом аппроксимирующий многочлен примет вид бесконечного ряда, называемого обобщенным рядом Фурье.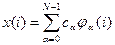 (3.12) – решетчатая функция. Для дискретных функций, удовлетворяющих условию
(3.12) – решетчатая функция. Для дискретных функций, удовлетворяющих условию 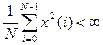 , справедлива следующая формула для определения спектра:
, справедлива следующая формула для определения спектра: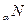 )]·
)]· 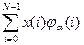 . (3.16)
. (3.16)


