
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы базисных функций (СБФ)
Один и тот же сигнал может быть разложен по различным СБФ или, что одно и то же, рассмотрен в различных системах координат. При этом внутренние закономерности сигналов не могут нарушаться при изменении системы координат. Однако спектральному анализу в различных СБФ соответствует различная физическая интерпретация и, что особенно важно, различная практическая реализация. При решении практических задач целесообразно подбирать наиболее подходящие СБФ. Выбор базиса во многом обусловлен спецификой решаемых задач и требованиями, предъявляемыми при их решении. Если задан ряд из N чисел X1, X2, …, Xk,…, XN,(1) то и функциональный базис следует выбрать из конечного набора N функций Фa (Х), a = 1, 2,…, N,(2) существующих на совокупности точек Xk. Тогда дискретное преобразование в этом базисе даст ровно N коэффициентов Ca, кoтoрыe находятся с помощью формального суммирования: Ca = S k Xk Фa (Xk), a = 1, 2,…, N. (3) Совокупность N коэффициентов Ca и составляет дискретное представление ряда чисел (1) в функциoнaльном базисе (2). Часто эту совокупность чисел Ca называют линейчатым спектром в выбранном базисе. Полных и ортогональных СБФ существует бесчисленное множество.
Такая система определена на целочисленном интервале [0, N). Система { u (i)} в форме (3.17) является ненормированной, и ее норма (корень квадратный из мощности)
Системы тригонометрический базисных функций. Система тригонометрических функций {cos(k), sin(k)} = { 1, sin(), cos(), sin(2 ), cos(2 ),...} является полной ортогональной системой с интервалом ортогональности [- , ], либо [0, 2 ]. Система является периодической с периодом 2 и ненормированной (норма равна 1/ Системы комплексных экспоненциальных функций. Полной ортогональной системой на интервале [- , ] или любом другом интервале длительностью 2 является система комплексных экспоненциальных функций. {ejkx} Это нормированная периодическая система с периодом 2 . Для нее характерно свойство мультипликативности, заключается в том, что произведение двух любых ее функций является также функцией этой системы: ejkx + ejmx = ejlx, где l = k + m. Дискретный аналог этой системы - система дискретных комплексных экспоненциальных функций {e2pki/N}, обладающая свойствами полноты, нормированности, ортогональности и мультипликативности на интервале, содержащим N отсчетов. Спектр c в этом базисе является комплексной функцией. Полиномиальные базисные системы. К ним относят системы, построенные на основе ортогональных полиномов. Полиномы Чебышева. На интервале [-1, 1] можно построить полную ортонормальную систему jn(x) = 2n(2p)-1/2 Tn(x), n=0,1,2,..., где Tn () - полиномы Чебышева, задаваемые следующим образом: T0 ()=1,
Полиномы Лежандра. Нормированные и ортогональные функции
Функции Уолша Для нормированных функций Уолша принято обозначение wal(n, ), где n - номер функции, а находится в интервале 0 <1. Обычно рассматривается множество функций Уолша wal(n, ) при n =0,1,..., N -1, где N =2 i и i =1,2,3,... Функции Уолша различают по их порядку и рангу. Под порядком понимают максимальный из содержащих единицу номеров разрядов при двоичном представлении числа n, рангом называют число единиц в двоичном выражении n. Например, порядок и ранг функции wal(5, ) равны соответственно 3 и 2, так как двоичным выражением числа 5 является 101. Функции Уолша могут быть упорядочены по Уолшу. Имеется упорядочивание функций Уолша по Пэли. Свойство симметрии: Wa (j / N) = Wj (a / N). Система Уолша-Пэли. Масштабирование данных. Во многих автоматизированных устройствах используются табличные данные. Одним из методов может быть метод сжатия табличной информации за счет ее спектрального разложения в некотором функциональном базисе. Более выгодным является использование для разложения базиса Уолша, так как для гладких функций коэффициенты разложения Уолша быстрее стремятся к нулю. Это допускает большую степень сжатия информации в базисе Уолша. Возможность сжатия информ. появляется, если число коэффициентов спектра можно сделать меньше числа N. Например, когда часть коэффициентов спектра равна нулю или близка к нему. Возможность сжатия информации и степень ее сжатия зависят как от самого ряда чисел, так и от набора функций, составляющих базис спектрального разложения Ca. Поскольку ряд чисел Хk нам задан, то управлять степенью сжатия мы можем, изменяя базис спектрального разложения. Функции Радемахера: R0 (z) = 1, Rk (z) = sign (sin (2 k p z)), k = 1,2,…, Наиболее интересной в плане сжатия информации является система функций Уолша-Пэли. Образование этой системы тесно связано с двоичными номерами составляющих ее функций. Конкретно, функция Уолша-Пэли с номером a есть произведение функций Радемахера с номерами тех двоичных разрядов a, в которых расположены 1. Если записать номер a в двоичном представлении с n = log N разрядами a = S k 2k-1 ak, то функции системы Уолша-Пэли можно представить так: Wa (z) = Pk [ Ra (z)] ak. Для проблемы сжатия исходной информации важна скорость убывания коэффициентов Ca разложения в базисе Уолша при росте номера a. Если функция, представляемая рядом (1), обладает непрерывной производной до m -го порядка, и максимальное значение модуля производной | X (m)| есть М, то коэффициенты спектра с номерами a, ранг которых не меньше порядка производной (r ³ m), удовлетворяет неравенству |C a (r ³ m)|< M / 2 m ( m +3)/2.
Именно это важное неравенство гарантирует быструю сходимость спектральных коэффициентов Ca с ростом номера a и открывает перспективы сжатия табличной информации. Действительно, ранг r функции Уолша увеличивается с ростом номера функции a так, что условие r ³ m выполняется для больших номеров a. Это значит, что оценка действует для финальных коэффициентов разложения. Чем меньше степень функции, которая порождает ряд чисел (l), тем большей степени сжатия можно достичь при разложении. Если ряд короткий, а степень велика, то сжатие вообще не достигается. Если при той же степени функции увеличивать число членов ряда и, следовательно, число коэффициентов спектра, то степень сжатия растет. 6.Классификация информационных сигналов. Сигналы. Модели процессов, аналитически представляющих сигнал. Аналитическое описание сигналов. Результаты обработки информации существенно зависят от выбора рациональной модели анализируемого сигнала. В зависимости от априорной информации о сигналах используются либо детерминированные, либо стохастические модели. Первые модели сигналов выражаются аналитическим описанием непосредственно самого изучаемого колебания (или функции), а вторые - описываются теми или иными вероятностными характеристиками и используются при анализе случайных процессов. Обычно в качестве детерминированных моделей используются следующие элементарные колебания: -импульс, функция включения (скачок) s (t)=1(t), треугольный импульс, гармонические функции sin (t), cos (t), отрезок гармонической функции, экспоненциальная функция exp (t), комплексно-экспоненциальная функция exp (jt), функция sin (t)/ t и другие. Детерминированные модели сигналов более сложного вида могут быть сформированы из элементарных путем линейных комбинаций. Одна из важных характеристик случайного процесса - это его частотная полоса. По этому признаку случайные процессы можно условно разделить на узкополосные и широкополосные. Чаще всего сигналы рассматривают как функции, заданные в определенных физических координатах. В этом смысле различают одномерные (например, зависящие от времени), двумерные, заданные на плоскости (примером могут служить различного рода изображения), трехмерные (характеризующие, например, пространственные объекты) сигналы. Математически такие сигналы описываются соответственно функциями одной, двух и трех переменных. Удобно применять и более сложные модели - комплексные и векторные функции.
Реальные сигналы всегда являются функциями с ограниченным интервалом определения. Так одномерный сигнал, с ограниченным интервалом определения можно записать в виде x (t), t [ tmin, tmax ], где tmin и tmax - соответственно нижняя и верхняя границы интервала определения. Если tmin и tmax - величины одного знака, то интервал определения будет односторонним, в противном случае интервал называется двусторонним. При tmin = - tmax интервал называется симметричным. Наряду с ограниченными по области определения сигналами в теории ИВС рассматриваются также сигналы, заданные на полубесконечном и бесконечном интервалах. Сигнал называется каузальным, если он имеет начало во времени. Все реальные сигналы являются каузальными. Сигнал называется периодическим, если любое его значение повторяется через интервалы, равные периоду. Финитным называется сигнал, равный нулю вне некоторого ограниченного интервала его определения. Все реальные сигналы могут рассматриваться как финитные. Непериодическим детерминированным сигналом называется любой детерминированный сигнал, для которого не выполняется условие: x (t) = x (t + kT), где период T является конечным отрезком, а k - любое целое число. Как правило, непериодический сигнал ограничен во времени. (прим. – импульсы, пачки импульсов, обрывки гармонических колебаний). Квазидетерминированный сигнал - это сигнал, закон изменения которого известен, но один или несколько параметров этого закона являются случайными величинами или процессами. В зависимости от формы представления сигналы могут быть непрерывными, квантованными по уровню, дискретными и цифровыми Формы представления сигнала
По характеру протекания во времени сигналы разделяются на два вида: - постоянные во времени; -переменные во времени. Переменные во времени - это сигналы, значение которых изменяется во времени. Сигнал называется случайным, если его значение в каждый момент времени есть случайная величина. Случайные сигналы делятся на: стационарные и нестационарные. У стационарных сигналов вероятностные характеристики не зависят от времени (постоянны). Стационарные сигналы, для которых вероятностные характеристики не зависят от способа усреднения (по времени и ансамблю) называются эргодическими.
Все случайные сигналы в итоге классифицируются по виду закона распределения плотности вероятности, который является полной и исчерпывающей характеристикой любого случайного сигнала.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 942; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.95 (0.026 с.) |

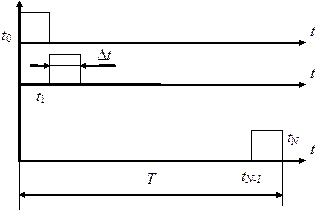 Системы единичных функций. Два прямоугольных импульса, не перекрывающие друг друга, ортогональны. Поэтому система прямоугольных импульсов, приставленных друг к другу и заполняющих интервал [ t 0, tN ], будет ортогональной системой.Такая система полна только для подмножества ступенчатых сигналов с шириной ступени t, где t - длительность импульсов, N = T / t - число импульсов на рассматриваемом интервале. Система таких функций будет полна для любого непрерывного сигнала при t 0 и N . В этом случае она превращается в систему единичных импульсов { u (t)}, имеющих единичную амплитуду и бесконечно малую длительность, положение которых определяется сдвигом по оси t = t при t 0, . Система функций { u (t)} является полной ортогональной системой.Из нее дискретизацией можно получить систему дискретных единичных функций { u (i)}, каждая из которых имеет вид единичного импульса бесконечно малой длительности и аналитически записывается в виде
Системы единичных функций. Два прямоугольных импульса, не перекрывающие друг друга, ортогональны. Поэтому система прямоугольных импульсов, приставленных друг к другу и заполняющих интервал [ t 0, tN ], будет ортогональной системой.Такая система полна только для подмножества ступенчатых сигналов с шириной ступени t, где t - длительность импульсов, N = T / t - число импульсов на рассматриваемом интервале. Система таких функций будет полна для любого непрерывного сигнала при t 0 и N . В этом случае она превращается в систему единичных импульсов { u (t)}, имеющих единичную амплитуду и бесконечно малую длительность, положение которых определяется сдвигом по оси t = t при t 0, . Система функций { u (t)} является полной ортогональной системой.Из нее дискретизацией можно получить систему дискретных единичных функций { u (i)}, каждая из которых имеет вид единичного импульса бесконечно малой длительности и аналитически записывается в виде

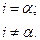 (3.17)
(3.17) Эта система представляет собой полную СБФ, служащую для разложения дискретных сигналов произвольной формы. Система дискретных единичных функций обладает тем свойством, что ее спектральный коэффициент с номером совпадает со значением сигнала в точке i = его интервала определения, т.е. ca = x ().
Эта система представляет собой полную СБФ, служащую для разложения дискретных сигналов произвольной формы. Система дискретных единичных функций обладает тем свойством, что ее спектральный коэффициент с номером совпадает со значением сигнала в точке i = его интервала определения, т.е. ca = x (). ). Проведя нормирование на ее основе, можно получить полную ортонормированную систему { 1,
). Проведя нормирование на ее основе, можно получить полную ортонормированную систему { 1, 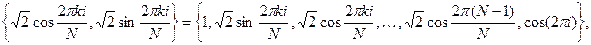 определенная на интервале [- N /2, N /2) или [0, N).
определенная на интервале [- N /2, N /2) или [0, N). . Полиномы Чебышева обладают важным свойством, из всех полиномов n -ой степени, имеющих коэффициент при n, равный единице, полином Чебышева Tn () наименее отклоняется от нуля на интервале [-1, 1].
. Полиномы Чебышева обладают важным свойством, из всех полиномов n -ой степени, имеющих коэффициент при n, равный единице, полином Чебышева Tn () наименее отклоняется от нуля на интервале [-1, 1]. ,
,  ,
,  образуют полную систему базисных функций на отрезке [-1,1]. Здесь { Pn ()} - полиномы Лежандра, определяемые по формуле
образуют полную систему базисных функций на отрезке [-1,1]. Здесь { Pn ()} - полиномы Лежандра, определяемые по формуле 
 Двоично-ортогональные системы базисных функций. Под этим условным названием объединены системы функций меандрового типа Радемахера, Уолша и Хаара, интервал ортогональности которых при их построении представляется совокупностью двоично-рационального числа равных подынтервалов. Эти системы имеют важное значение для практики спектральной обработки, поскольку принимают только значения 1 (функция Радемахера и Уолша) либо 1 и 0 (функция Хаара) и легко могут быть получены с помощью цифровых устройств. Все эти системы взаимосвязаны друг с другом и каждую из них можно получить из другой, образуя соответствующую линейную комбинацию.
Двоично-ортогональные системы базисных функций. Под этим условным названием объединены системы функций меандрового типа Радемахера, Уолша и Хаара, интервал ортогональности которых при их построении представляется совокупностью двоично-рационального числа равных подынтервалов. Эти системы имеют важное значение для практики спектральной обработки, поскольку принимают только значения 1 (функция Радемахера и Уолша) либо 1 и 0 (функция Хаара) и легко могут быть получены с помощью цифровых устройств. Все эти системы взаимосвязаны друг с другом и каждую из них можно получить из другой, образуя соответствующую линейную комбинацию.






