Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результаты девяти аналогичных опытов
Примечание. При проведении опытов увеличивали открытие крана, чтобы разность показаний пьезометров (потеря напора по длине) возрастала примерно в 1,5– 1,6 раза. Контрольные вопросы 1. Перечислите режимы движения жидкости и укажите их характерные особенности. 2. Что такое критерий Рейнольдса? Укажите факторы, от которых он зависит. 3. Что такое критическое число Рейнольдса? 4. Как и с какой целью определяется режим движения жидкости при гидравлических расчетах? 5. Что такое критическая скорость? От каких факторов она зависит? Как определяется критическая скорость? 6. Напишите и поясните аналитические зависимости потерь напора по длине от средней скорости потока при ламинарном и турбулентном режимах движения жидкости. 7. Изобразите график зависимости потерь напора по длине от средней скорости (в логарифмических координатах) и опишите его.
Цели работы: 1. Определить на опыте коэффициент гидравлического трения и коэффициент местного сопротивления для трех его видов; 2. Используя соотношения А.Н. Альтшуля или же график Никурадзе, установить области гидравлического сопротивления участков напорного трубопровода; 3. Вычислить коэффициенты гидравлического трения по эмпирическим формулам; 4. Найти справочные значения коэффициентов местных сопротивлений; 5. Оценить сходимость расчетного коэффициента сопротивления по длине и местных сопротивлений с их справочными значениями. Теоретические положения
Экспериментальными исследованиями установлено, что при движении жидкости часть полного напора (энергии) затрачивается на преодоление работы вязких и инерционных сил, т.е. возникают потери напора. При равномерном движении жидкости гидравлическое сопротивление, проявляющееся равномерно по всей длине потока, называют сопротивлением по длине, а вызываемые им потери напора ‑ потерями напора по длине (hl).Эти потери в круглых трубопроводах, работающих полным сечением, вычисляют по формуле Дарси – Вейсбаха:
где l – безразмерный коэффициент, называемый коэффициентом гидравлического трения (коэффициентом Дарси). Значение коэффициента l характеризует гидравлическое сопротивление трубопровода и зависит в общем случае от числа Рейнольдса Re и относительной шероховатости Dэ / d трубопровода, т.е. l = f (Rе, Dэ/ d); l, d – длина и внутренний диаметр трубопровода; Значение коэффициента l при гидравлических экспериментах вычисляют по опытным данным из формулы (4.1), при гидравлических расчетах – по эмпирическим и полуэмпирическим формулам (например, при ламинарном режиме lп = 64/Rе), при турбулентном режиме движения и работе трубопровода в области доквадратичного сопротивления – по формуле А.Д. Альтшуля:
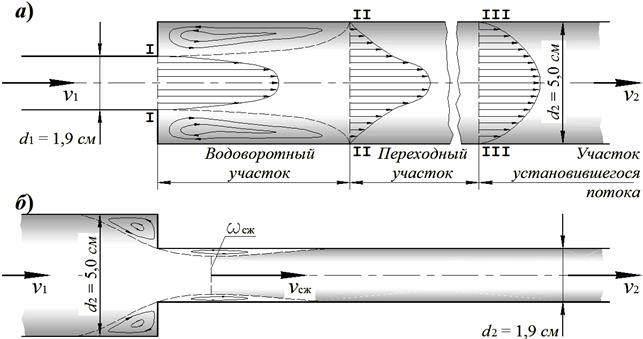
Значение абсолютной эквивалентной шероховатости Dэ при расчетах берут из справочной литературы в зависимости от материала трубопровода и состояния его внутренней поверхности. Например, для труб из органического стекла Dэ = 0,006 мм, а для стальных водопроводных умеренно заржавленных труб Dэ = = 0,20¸0,50 мм. Область гидравлического сопротивления при расчетах определяют или по графикам l = f (Re, Dэ / d) непосредственно, полученным опытным путем для труб из различных материалов и приведенным в справочной литературе, например, по графику Никурадзе (рис. 4.1), или же с помощью соотношений Вычисляют соотношения 10 d / Dэ и 500 d / Dэ и сравнивают их значения с числом Рейнольдса Re = υ d / n. При этом если При гидравлических расчетах в каждой области гидравлического сопротивления предложены и используются свои формулы для вычисления коэффициента l. Другой вид гидравлических сопротивлений, возникающих в местах резкого изменения конфигурации потока, – местные сопротивления, а вызываемые ими потери напора – местные потери напора (h м). При прохождении через любое местное сопротивление поток жидкости деформируется (рис. 4.2, а, б), – он становится неравномерным, резко изменяющимся. Для него характерны: 1) значительные искривления линий тока; 2) отрывы транзитной струи от стенок трубопровода (действие сил инерции) и возникновение в местах отрыва устойчивых водоворотов; 3) повышение пульсации скоростей и давлений (по сравнению с равномерным движением); 3) изменение формы (переформирование) эпюр скоростей.
Рис. 4.1. График зависимости коэффициента гидравлического трения l от числа Рейнольдса Re для труб с различной относительной шероховатостью D / d (график Никурадзе): I – I – зона вязкостного сопротивления; II – II – область гидравлически гладких труб; II – II и АВ – область доквадратичного сопротивления; область справа от АВ – область квадратичного сопротивления
Рис. 4.2. Схемы движения жидкости при резком изменении сечения трубопровода: а – резкое расширение трубопровода; б – резкое сужение Местные потери напора при гидравлических расчетах определяют по формуле Вейсбаха:
где Значение коэффициента ζ зависит в общем случае от числа Рейнольдса Re и от конфигурации, т.е. от формы проточной части местного сопротивления. В частности, если трубопровод, на котором расположено местное сопротивление, работает в области квадратичного сопротивления, то значение коэффициента ζ не зависит от Re. Значение ζ для каждого вида местного сопротивления определяют по данным гидравлических экспериментов, пользуясь формулой (4.3). Полученные таким образом значения коэффициентов ζ для различных видов местных сопротивлений (обычно в области квадратичных сопротивлений) для гидравлических расчетов приводятся в справочной и специальной литературе. Исключением являются резкое расширение и резкое сужение трубопровода (см. рис. 4.2, а, б), для которых численные значения координаты ζ определяются по формулам, полученным теоретически. Так, если трубопровод резко расширяется, средняя скорость в формуле (4.3) взята перед местным сопротивлением υ 1,
если же скорость берется за местным сопротивлением, т.е. υ 2, то
Коэффициент ζр. с сопротивления при резком сужении трубопровода принято относить к скорости после сужения. При этом
где Описание установки
Установка (рис. 4.3) представляет собой систему напорных трубопроводов с последовательно расположенными на ней гидравлическими сопротивлениями (по длине и местными). К каждому гидравлическому сопротивлению подключены по 2 пьезометра (до и после него). Все пьезометры для удобства выведены на щит 1.
Рис. 4.3. Схема установки для измерения гидравлических сопротивлений по длине и местных: 1 – ряд пьезометров, закрепленных на щите; 2 – вентиль;
Для регулирования расхода Q воды в системе служит вентиль 2. Значение Q измеряется с помощью мерного бака 3 и секундомера 4. Подача воды в систему осуществляется из питающего резервуара 4 по трубе 5. Постоянный уровень воды в резервуаре 4 (для обеспечения установившегося движения воды в системе труб) поддерживается переливным устройством. Вода в резервуар 4 подается центробежным насосом. Порядок выполнения работы и обработка
При закрытом вентиле 2 нужно включить насос и обеспечить подачу воды в питающий резервуар 5. После наполнения резервуара водой и стабилизации уровня воды (переливное устройство должно начать работать) плавным открытием вентиля 2 следует подать воду в систему трубопроводов. Далее необходимо измерить: отметки уровней воды во всех пьезометрах, расход воды в системе (с помощью мерного бака 3 и секундомера 4), а также ее температуру (термометром в резервуаре 5). Результаты измерений для двух опытов (при разных расходах воды) записать в табл. 1.7. Обработать опытные данные и результаты представить в виде таблицы. Сделать выводы по результатам работы. Контрольные вопросы 1. Напишите и поясните формулы Дарси – Вейсбаха и Вейсбаха. 2. Как опытным путем определяются значения коэффициентов l и ζ? 3. Что характеризуют коэффициенты l и ζ? 4. От каких факторов в общем случае зависят коэффициенты l и ζ? 5. Как определяются коэффициенты l и ζ при гидравлических расчетах? 6. Что такое Dэ и Dэ/ d? Как найти значение Dэ при гидравлических расчетах? 7. Укажите области гидравлического сопротивления трубопроводов. 8. Как определяется область сопротивления при гидравлических расчетах? 9. Изобразите схемы движения жидкости при резком повороте трубы на 90°, а также при резком расширении и резком сужении трубопровода и дайте пояснения к ним. 10. Что характерно для движения потока при протекании его через любое местное сопротивление?
Цели работы: 1. Определить экспериментально характерные коэффициенты при истечении жидкости через малое круглое отверстие диаметром 2 см при постоянном напоре в атмосферу и такие же коэффициенты для внешних насадков: цилиндрического и конического (сходящегося и расходящегося); 2. Сравнить значения коэффициентов, полученные экспериментально, со справочными значениями и подсчитать относительные отклонения. Теоретические положения Малым считается отверстие, вертикальный размер которого (для круглой трубы – диаметр d) не превышает 0,1 его глубины h. Здесь глубина (h) ‑ превышение свободной поверхности жидкости над центром отверстия. Стенку считают тонкой, если ее толщина d < (1,5…3,0) d (рис. 5.1). При выполнении этого условия значение d не влияет на характер истечения жидкости из отверстия, так как вытекающая струя жидкости касается только острой кромки отверстия. Поскольку частицы жидкости движутся к отверстию по криволинейным траекториям, из-за сил инерции струя, вытекающая из отверстия, сжимается. Благодаря действию сил инерции струя продолжает сжиматься и после выхода из отверстия. Наибольшее сжатие струи, как показывают опыты, наблюдается в сечении С ‑ С на расстоянии, примерно равном 0,5¸1,0 d входной кромки отверстия (см. рис. 5.1). Это сечение называют сжатым. Степень сжатия струи в этом сечении оценивают коэффициентом сжатия e:
где wс и w – соответственно площадь сжатого живого сечения струи и площадь отверстия.
Рис. 5.1. Истечение жидкости из малого отверстия в тонкой стенке
Среднюю скорость струи V c в сжатом сечении С – С при р 0 = р ат вычисляют по формуле, полученной из уравнения Д. Бернулли, составленного для сечений I – I и С – С (см. рис. 5.1):
где j – коэффициент скорости отверстия:
Согласно уравнению баллистической траектории струи, вытекающей из отверстия, получено выражение для коэффициента j:
В формулах(5.3) и (5.4) a – коэффициент Кориолиса; z – коэффициент сопротивления отверстия; xi и yi – координаты произвольно взятой точки траектории струи. Поскольку напор теряется главным образом вблизи отверстия, где скорости достаточно велики, при истечении из отверстия учитывают только местные потери напора. Расход жидкости Q через отверстие равен
где
Здесь m – коэффициент расхода отверстия, учитывающий влияние гидравлического сопротивления и сжатия струи на расход жидкости. С учетом выражения для m формула (5.5) принимает вид
Значения коэффициентов e, z, j, m для отверстий определяются опытным путем. Установлено, что они зависят от формы отверстия и числа Рейнольдса. Однако при больших значениях числа Рейнольдса (Re ³ 105) указанные коэффициенты не зависят от Re и для круглых и квадратных отверстий при совершенном сжатии струи они равны: e = 0,62¸0,64; z = 0,06; j= 0,97¸0,98; m = 0,60¸0,62. Насадкой называют патрубок длиной 2,5 d £ LH £ 5 d (рис. 5.2), присоединенный к малому отверстию в тонкой стенке с целью изменения гидравлических характеристик истечения (скорости, расхода, траектории струи жидкости).
Рис. 5.2. Истечение воды из насадков различных типов: а – внешние цилиндрические; б – внутренние цилиндрические; в – конические сходящиеся;
Насадки бывают цилиндрические (внешние и внутренние), конические (сходящиеся и расходящиеся) и коноидальные, т.е. очерченные по форме струи, вытекающей из отверстия. Использование насадка любого типа вызывает увеличение расхода Q жидкости благодаря вакууму, возникающему внутри насадка в области сжатого сечения С–С и обусловливающему повышение напора истечения. Среднюю скорость V истечения жидкости из насадка и расход Q определяют по формулам, полученным из уравнения Д. Бернулли, записанного для сечений 1–1 и В–В (см. рис. 5.2).
Здесь Для выходного сечения В–В коэффициент сжатия струи e = 1 (насадка в этой области работает полным сечением), поэтому коэффициент расхода насадки mн = jн. Расход жидкости, вытекающей из насадки, вычисляют по формуле, аналогичной (5.7):
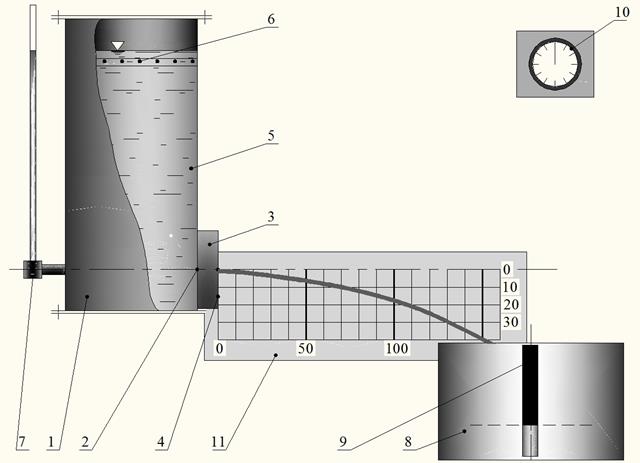
Описание установки Установка (рис. 5.3) представляет собой напорный резервуар 1, в боковой поверхности которого имеется отверстие 2, закрываемое рычажным клапаном 3. Перед отверстием 2 (снаружи резервуара 1) смонтирован поворотный круг 4 с отверстиями различной формы и насадками различных типов. Поворачивая круг, можно установить против отверстия 2 насадок нужного типа или отверстие требуемой формы. Воду 5 в резервуар 1 подают по трубопроводу открытием задвижки. Постоянный уровень воды в резервуаре 1 во время опытов поддерживается переливной трубой (не показано), а ослабление возмущений, создаваемых поступающей в него водой, осуществляется успокоительными решетками 6. Для определения напора h истечения воды резервуар 1 снабжен водомерной трубкой 7 (пьезометром) со шкалой, нулевая отметка которой совпадает с центром отверстия 2. Расход воды, истекающей из отверстий и насадков, измеряют с помощью широкого и передвижного мерного бака 8 снабжен водомерным стеклом 9 и секундомера 10. Координаты X и Y произвольных точек траектории струи измеряют с помощью координатного планшета 11.
Рис. 5.3. Установка для экспериментального изучения характера истечения жидкости из отверстий и насадков
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.139.50 (0.005 с.) |

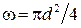

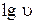



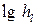
 (см. справочник)
(см. справочник)
 (4.1)
(4.1) – средняя скорость движения потока жидкости.
– средняя скорость движения потока жидкости. . (4.2)
. (4.2)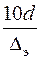 и
и 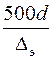 , предложенных А.Д. Альтшулем на основании использования этих графиков. В последнем случае поступают следующим образом.
, предложенных А.Д. Альтшулем на основании использования этих графиков. В последнем случае поступают следующим образом.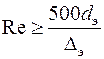 , то трубопровод работает в области гидравлически гладких труб. Если
, то трубопровод работает в области гидравлически гладких труб. Если  , то трубопровод работает в области квадратичного сопротивления. Если 10 d / Dэ < Re < 500 d э/Dэ, то трубопровод работает в области доквадратичного сопротивления.
, то трубопровод работает в области квадратичного сопротивления. Если 10 d / Dэ < Re < 500 d э/Dэ, то трубопровод работает в области доквадратичного сопротивления.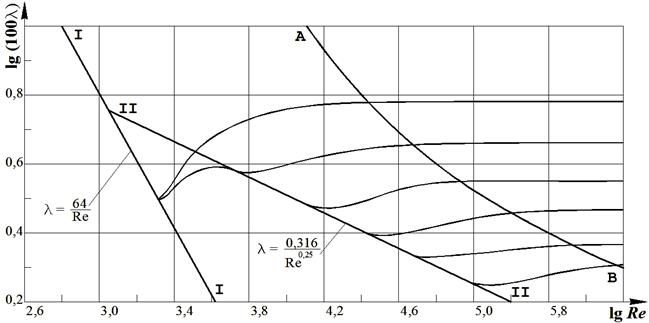
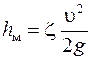 , (4.3)
, (4.3)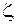 – коэффициент местного сопротивления (безразмерный);
– коэффициент местного сопротивления (безразмерный); 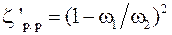 , (4.4)
, (4.4)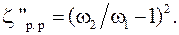 (4.5)
(4.5) , (4.6)
, (4.6)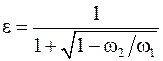 – коэффициент сжатия струи.
– коэффициент сжатия струи.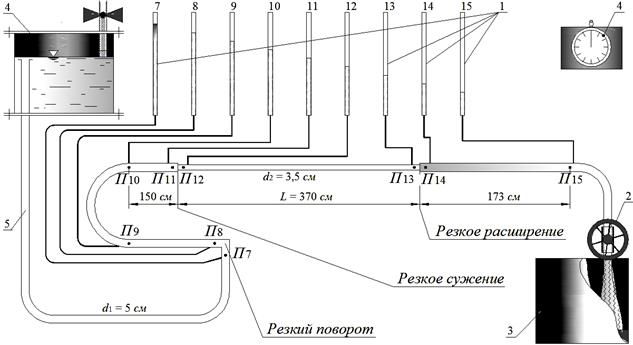
 Таблица 1.7
Таблица 1.7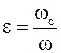 , (5.1)
, (5.1)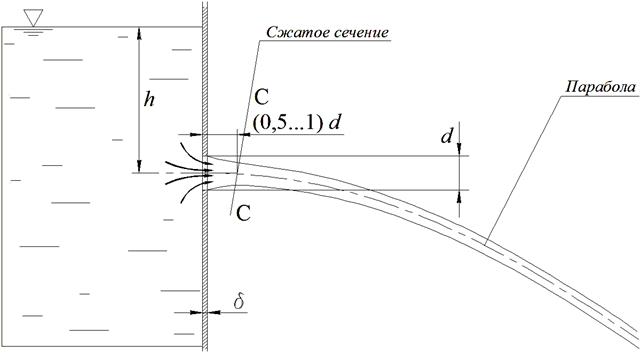
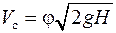 , (5.2)
, (5.2)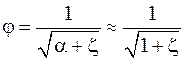 . (5.3)
. (5.3) . (5.4)
. (5.4) (5.5)
(5.5)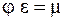 . (5.6)
. (5.6)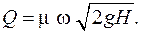 (5.7)
(5.7)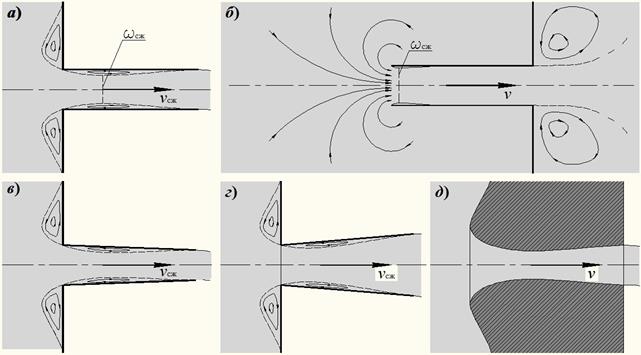
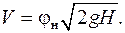 (5.8)
(5.8) – коэффициент скорости насадки; zн – коэффициент сопротивления насадки.
– коэффициент скорости насадки; zн – коэффициент сопротивления насадки.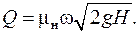 (5.9)
(5.9)