Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок проведения практических занятий
Практические занятия предназначены для изучения закона Паскаля и уравнений Д. Бернулли, а также влияния основных гидравлических параметров на гидростатические и гидродинамические процессы. На каждом практическом занятии студент должен: 1) восстановить знания из курса лекций, прочитав и усвоив теоретические сведения; 2) выполнить задание, вычертив схему изучаемого процесса и сделав необходимые расчеты; 3) ответить на контрольные вопросы; 4) оформить отчет по проделанной работе в соответствии с принятыми в ЧГУ правилами; 5) представить отчет преподавателю для его защиты, объяснить ход расчетов, сделать обоснованные выводы; 6) ответить на дополнительные контрольные вопросы; 7) получить оценку по данному практическому занятию.
Лабораторная работа 1 ИЗМЕРЕНИЕ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ
Цели работы: измерить с помощью пружинных манометров гидростатическое давление в трех точках (А, В и С), расположенных на различной глубине под уровнем жидкости, находящейся в абсолютном покое под действием только силы тяжести; подтвердить на основании экспериментальных данных закон Паскаля; построить по данным опыта № 2 в масштабе эпюру манометрического давления по глубине h. Теоретические положения
Гидростатическим давлением p называют нормальное сжимающее напряжение, возникающее в покоящейся жидкости под действием поверхностных и массовых сил:
где Δ P – элементарная равнодействующая поверхностных и массовых сил (гидростатическая сила), Н; Δ S – элементарная площадка действия, м2. Из формулы (1.1) видно, что гидростатическое давление p есть предел отношения элементарной гидростатической силы Δ P к элементарной площади Δ S ее действия, когда площадь последней стремится к нулю. За единицу гидростатического давления принято равномерно распределенное давление, создаваемое силой в 1 Н на площади в 1 м2, т.е.
Гидростатическое давление, отсчитываемое от 0, называют абсолютным (p абс), а отсчитываемое от атмосферного (p атм) – избыточным (p изб). Следовательно,
Очевидно, что
Из формулы (1.3) видно, что в зависимости от соотношения между p абс и p изб избыточное давление p изб может быть и положительным, и отрицательным. Положительное избыточное давление называют манометрическим, а отрицательное – вакуумметрическим. Приборы для их измерения называют соответственно манометрами и вакуумметрами.
По принципу действия манометры и вакуумметры делятся на 2 группы: жидкостные и механические. Жидкостный манометр (пьезометр) – стеклянная трубка, верхний ее конец открыт в атмосферу, а нижний –подключен к точке, где измеряют избыточное давление (рис. 1.1). Механические (пружинные) манометры в технике применяют весьма часто (рис. 1.2). В гидравлических расчетах величину нормального атмосферного давления считают равной p атм = 98 100 Па (760 мм рт. ст. ≈ Сравнительно небольшое давление, в том числе атмосферное, обычно измеряют барометром (рис. 1.3).
Манометрическое давление, выраженное через показания манометра:
где ρ g = γ – объемный вес жидкости; Действие механических приборов основано на деформации под действием давления упругого элемента (пружины или мембраны). Пружинный манометр показывает давление в точке жидкости на уровне оси вращения его стрелки. Если положения оси вращения стрелки и точки подключения манометра по высоте не совпадают (± y) (рис. 1.4), то в показание манометра (p м) вводят поправку (± ρ gy).
Для случаев, изображенных на рис. 1.4,
где y – превышение оси вращения стрелки манометра над точкой его подключения, м. В этой лабораторной работе предусмотрено измерение манометрического давления пружинными манометрами.
Когда на покоящуюся жидкость действует только сила тяжести, распределение гидростатического давления p по глубине h (см. рис. 1.1) описывается основным уравнением гидростатики, выражающееся следующей линейной функцией:
где p – гидростатическое давление в жидкости на глубине h (функция), Па; p 0 – внешнее давление, т.е. гидростатическое давление на свободной поверхности жидкости (свободный член), Па; h – глубина погружения в жидкость рассматриваемой точки (аргумент), м; ρ g – удельный вес жидкости (коэффициент), Н. Из уравнения (1.6) видно, что при p 0 = const и ρ = const давление p с изменением значения h изменяется по линейному закону (см. рис. 1.3). Уравнение (1.6) – линейное, т.е. его каноническая форма ах + b = 0 показывает, что функция p (давление) с изменением аргумента h (глубины) изменяется по линейному закону с коэффициентом a = ρ g (удельный вес жидкости). Из уравнения (1.6) следует, что внешнее давление p 0 в покоящейся жидкости распространяется по всем направлениям равномерно (закон Паскаля). Справедливость этого закона предстоит проверить на опыте, т.е. экспериментально. Описание установки
Установка (см. рис. 1.4) представляет собой толстостенный стальной цилиндр 1, частично заполненный водой, уровень которой измеряется водомерной трубкой со шкалой 2. Для изменения гидростатического давления над свободной поверхностью жидкости в точке А и в точках В и С подключения 4, заглубленных под уровень соответственно на hА, hВ и hС, посредством трубок 5 подключены пружинные манометры 3 (MA, MB и MC). В пространство над свободной поверхностью жидкости можно подавать сжатый воздух от компрессора 6 по трубопроводу. Для сброса избыточного гидростатического давления в цилиндре служит вентиль 7. В крышке цилиндра должен иметься предохранительный клапан, отрегулированный на давление, примерно равное 500 кПа, и вентиль 8 сообщения с атмосферой. Порядок выполнения работы и обработка результатов Необходимо выполнить два опыта, обеспечив в первом Опыт 1.Открыть вентиль 6 для обеспечения Таблица 1.1
Примечание.1, 2 – индексы, применяемые в обозначениях гидростатического давления (см. позицию 3 табл. 1.1), указывающие номер опыта. Опыт 2. Закрыть вентиль 6, а вентиль 7 открыть. Затем включить компрессор 1 для подачи сжатого воздуха в цилиндр 1. Довести Вычисляя по уравнению давление p в нескольких точках, заглубленных на различную величину h, построить диаграмму распределения гидростатического давления p по глубине h, называемую эпюрой гидростатического давления (рис. 1.5).
Выполнить все вычисления, предусмотренные табл. 1.1. Дать заключение по результатам работы. Контрольные вопросы Основные 1. Что такое гидростатическое давление и каковы его свойства? 2. Что такое абсолютное и избыточное гидростатическое давление и какова связь между ними? 3. Дайте определения понятий «внешнее давление» и «весовое давление». 4. Напишите и поясните основное уравнение гидростатики. 5. Поясните связь основного закона гидростатики с законом Архимеда. 6. Сформулируйте закон Паскаля. 7. Что такое пьезометрическая высота? 8. Опишите устройство и принцип действия барометра. 9. В чем заключается принципиальное отличие условий проведения 1-го и 2-го опытов? 10. Для чего нужно знать превышение оси вращения стрелки пружинного манометра над точкой его подключения? Дополнительные 11. Приведите примеры внешнего давления. 12. В чем заключается различие между понятиями «удельный вес жидкости» и «плотность жидкости»? 13. Какова связь основного уравнения гидростатики с законом сообщающихся сосудов? 14. Как называются приборы для измерения избыточного гидростатического давления? Сформулируйте их принципы действия. 15. Когда и с какой целью применяют ртутные и водяные пьезометры? В чем принципиальное различие между ними?
16. Какая величина принята за стандарт для атмосферного давления на уровне моря?
Цели работы: 1. Определить опытным путем слагаемые z, p / r g, U 2 / 2 g уравнения Д. Бернулли для сечений I – I и II – II, а также потери полного напора h ' w 1–2 между сечениями (рис. 2.1). 2. Вычислить средние скорости потока и отвечающие им скоростные напоры U 2/2 g для указанных живых сечений потока жидкости. 3. Построить в масштабе по опытным данным пьезометрическую линию и линию полного напора (см. рис. 2.1).
Теоретические положения
Сечение потока жидкости называется живым, если все линии тока (струйки), проходящие через него, в каждой его точке нормальны к нему. Для двух произвольно выбранных живых сечений I – I и II – II струйки реальной жидкости (рис. 2.1) при установившемся движении справедливо уравнение Д. Бернулли:
Рис. 2.1. Диаграмма уравнения Д. Бернулли для струйки реальной жидкости: 0 – 0 – плоскость сравнения; 1 – линия полной удельной энергии (полного напора); 2 – линия удельной потенциальной энергии (пьезометрическая линия); Слагаемые, входящие в уравнение (2.1), можно истолковать с геометрической и энергетической точек зрения. С геометрической точки зрения слагаемые уравнения (2.1) – высоты (напоры): Z – геометрическая высота (напор), т.е. превышение центра тяжести рассматриваемого поперечного сечения струйки над плоскостью сравнения 0 – 0, выбираемой произвольно (см. рис. 2.1); р /r g – пьезометрическая высота, т.е. высота подъема жидкости в пьезометре, подключенном к центру тяжести рассматриваемого сечения струйки, отвечающая гидродинамическому давлению р в этой точке; U 2 / 2 g – скоростная высота (скоростной напор), отвечающая местной скорости U, т.е. скорости в центре тяжести сечения; при этом
С энергетической точки зрения, слагаемые уравнения (2.1) представляют собой разновидности удельной энергии, а именно: Z – удельная потенциальная энергия положения жидкости в рассматриваемом сечении струйки в поле тяжести земли; р /r g – удельная потенциальная энергия давления; U 2 / 2 g – удельная кинетическая энергия;
h ' w 1–2 – потеря полной удельной энергии струйки, т.е. ее часть, затраченная на преодоление работы сил внутреннего трения, обусловленного вязкостью жидкости. Удельной энергией называется энергия, приходящаяся на единицу веса жидкости. Значения слагаемых уравнения (2.1) могут быть определены опытным путем следующим образом: Z ‑ геометрическим нивелированием, или же измерением линейкой;
p /r g ‑ с помощью пьезометрической трубки (пьезометра); U 2 / 2 g ‑ по разности отметок уровней жидкости в скоростной и пьезометрической трубках, подключенных к рассматриваемой точке живого сечения струйки (рис. 2.2); h ` w 1–2 ‑ по разности отметок уровней жидкости в скоростных трубках, подключенных к сечениям I – I и II – II (см. рис. 2.1).
Рис. 2.2. К измерению скоростного напора: а – напорное движение жидкости в трубопроводе; б – безнапорное движение жидкости в открытом водоеме; u – местная скорость; 1 – пьезометр; 2 – скоростная трубка; 0 – 0 – плоскость
Скоростная трубка (рис. 2.2) представляет собой трубку, верхний конец которой открыт в атмосферу, а нижний – изогнут навстречу потоку жидкости в рассматриваемой точке. Благодаря этому у входа в изогнутый конец скоростной трубки кинетическая энергия частицы потока жидкости преобразуется в потенциальную энергию давления столба жидкости высотой hu = U 2 / 2 g в этой трубке. Поскольку срез нижнего конца скоростной трубки перпендикулярен вектору скорости, а срез нижнего конца пьезометра параллелен ему (см. рис. 2.1), уровень жидкости в скоростной трубке всегда устанавливается выше (на величину U 2/2 g), чем в пьезометре. Прибор, конструктивно объединяющий пьезометрическую (П) и скоростную (С) трубки, называется трубкой Пито и широко применяется для измерения скорости движения жидкости Уравнение Д. Бернулли для двух сечений потока реальной жидкости:
где Значение a зависит от режима течения жидкости, а также от вида движения. Так, при равномерном движении для ламинарного режима a = 2,0, а для турбулентного режима a = 1,05 … 1,15. Живое сечение потока жидкости – сечение, в каждой своей точке нормальное к элементарным линиям тока жидкости. Если поток жидкости сужается, то его живое сечение вогнуто; если поток расширяется, то его живое сечение направлено выпуклостью вперед. Слагаемые уравнений (2.1) и (2.2) в различных живых сечениях можно изображать графически в виде диаграммы уравнения Д. Бернулли (графика напоров) (см. рис. 2.1), дающей наглядное представление о перераспределении по пути движения жидкости потенциальной и кинетической энергии, а также о характере убывания полной энергии. Описание установки Установка (рис. 2.3) представляет собой напорный бак 1 спереливным устройством 2 и питателем 3 трубопровода, трубопроводом 4, снабженном пьезометрами 5 и скоростными трубками 6, вентилем 7 регулировки расхода воды в трубопроводе. Для отметки высот служит шкала 8. Для фиксации расхода служит мерный бак 9. Имеется секундомер 10. Установка предназначена для исследования установившегося движения жидкости. Сечения I – I, II – II и III – III трубопровода имеют диаметры: d 1 = 2,8 см; d 2 = 1,8 см; d 3 = 2,8 см.
Рис. 2.3. Установка для экспериментальной проверки уравнения Д. Бернулли Порядок выполнения работы и обработка полученных
1. При закрытом вентиле 7 открыть питатель 3 для заполнения бака 1 и трубопровода 4 водой. При этом следует обратить внимание на уровни воды в пьезометрических 5 и скоростных трубках 6. Эти уровни при отсутствии воздуха в системе должны быть на одной отметке. 2. Открыть вентиль 7 так, чтобы трубопровод 4 работал полным сечением, а уровень воды в баке 1 был постоянным. 3. Измерить с помощью бака 9 и секундомера 10 расход воды. 4. Линейкой измерить геометрические высоты z центров тяжести сечений I – I, II – II и III–III относительно плоскости сравнения 0 – 0, отмеченной на установке. 5. Определить по шкалам отметки уровней воды в пьезометрах и скоростных трубках в сечениях I – I, II – II и III – III. Результаты всех измерений записать в табл. 2.1. 6. Выполнить все вычисления, предусмотренные табл. 2.1, и построить в масштабе по полученным данным линию полного напора и пьезометрическую линию (см. рис. 2.1). 7. Дать заключение по результатам проделанной работы.
Таблица 2.1 Измеряемые и вычисляемые величины для построения
Продолжение табл. 2.1
Примечания: 1. Для сечения III – III (см. графу 6) числовые значения величин (см. позиции 5 и 8–13) те же, что и для сечения II – II; 2. Потери полного напора h ' w (см. позицию 6) между сечениями II – II и III – III принять равными потерям напора между сечениями I – I и II – II; 3. Остальные величины для сечения III – III (см. позиции 1–4) следует определить с привлечением уравнения Д. Бернулли [см. уравнение (2.2)].
Контрольные вопросы
1. В чем заключается энергетический смысл слагаемых уравнения Д. Бернулли. 2. Как называется коэффициент a, входящий в уравнение Д. Бернулли для потока реальной жидкости, что он учитывает и от чего зависит? 3. Чем обусловлены потери полного напора и каков их энергетический смысл? 4. Дайте определение понятия «удельная энергия». 5. Дайте определения понятий «местная скорость» и «средняя по сечению скорость». 6. Как определяются экспериментально местную скорость и среднюю по сечению скорость? 7. Что такое скоростная трубка? 8. Что такое трубка Пито? 9. Что такое линия полного напора и пьезометрическая линия? 10. Что представляют собой эти линии при равномерном движении реальной жидкости? 11. Дайте определение понятия «живое сечение потока жидкости».
Цели работы: 1. Убедиться на опыте при окрашивании струйки воды в стеклянной трубе в существовании ламинарного и турбулентного режимов течения жидкости; 2. Вычислить по данным опытов значения числа Рейнольдса при ламинарном и турбулентном режимах, сравнить их с критическим значением, убедиться, что при ламинарном режиме Rе < Reкр, а при турбулентном Re > Reкр; 3. Построить по опытным данным график lg h e = f (lg υ), определить с его помощью критическую скорость υ кр, а через нее вычислить Reкр = 2320; 4. Подтвердить с помощью графика lg hl Теоретические положения Многочисленными экспериментальными исследованиями установлено, что движение жидкости может происходить или при ламинарном, или при турбулентном режиме. Ламинарный режим наблюдают при небольших скоростях, когда окрашенные струйки жидкости не перемешиваются, сохраняясь по всей длине потока, т.е. движение жидкости при ламинарном режиме – струйчатое, перемешивание слоев жидкости отсутствует. Турбулентный режим наблюдают при значительных скоростях. Он характерен интенсивным перемешиванием жидкости; при этом скорости и давления пульсируют. Средняя скорость потока, при которой происходит смена режима движения жидкости, называется критической (υ кр). Как показывают опыты в трубопроводах круглого сечения, ее значение зависит от рода жидкости, характеризуемого динамической вязкостью m, плотностью ρ, и от диаметра d трубопровода. Одновременно опытами установлено, что безразмерный алгебраический комплекс, отвечающий критической скорости υ кр, равен
и не зависит от m, r и d. Число Reкр( d ) = 2320 называется критическим числом Рейнольдса. Устойчивый ламинарный режим наблюдается при значениях числа Рейнольдса Таким образом, число Рейнольдса
является критерием, позволяющим судить о режиме движения жидкости в круглой трубе, работающей полным сечением. Параметр u = m/r, входящий в формулы (3.1) и (3.2), называют кинематическим коэффициентом вязкости жидкости. Из изложенного следует, что для определения режима движения жидкости в круглом трубопроводе при напорном движении жидкости достаточно по формуле (3.2) вычислить число Рейнольдса и сравнить его с критическим значением. Знание режима движения жидкости необходимо для правильной оценки потерь напора (рис. 3.1).
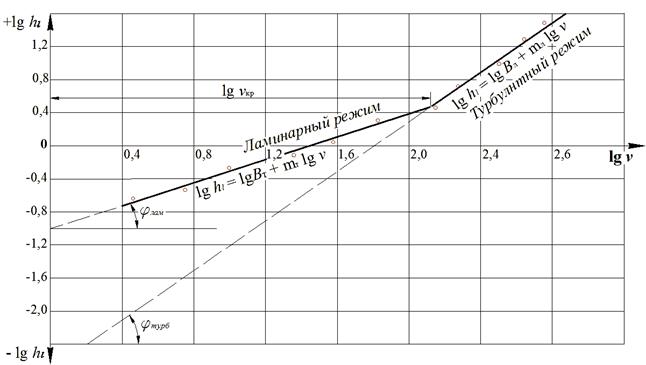
Рис. 3.1. График зависимости потерь напора по длине круглой трубы hl от средней скорости υ жидкости в логарифмической системе координат
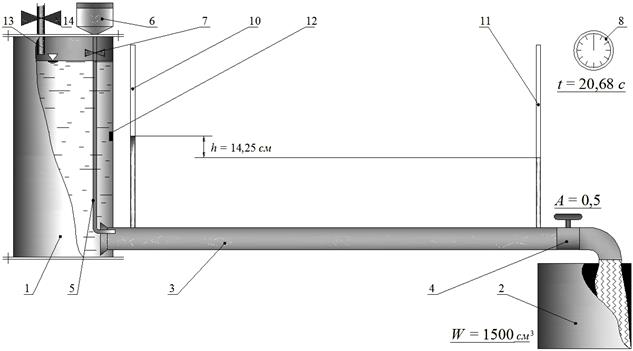
При ламинарном режиме потери напора hl пропорциональны средней скорости v в первой степени, а при турбулентном – в степени 1,75 < m > 2,0. Заметим, что с помощью этого графика определяют значение критической скорости v кр, а через нее – и критическое число Рейнольдса по формуле (3.1). Описание установки Установка включает в себя (рис. 3.2) напорный бак 1, мерную емкость 2 и две горизонтальные трубы: широкую 3 (d = 1,6 cм), в которой и изучается движение воды при различных режимах, с регулировочным краном 4, и тонкую (d = 0,9 см) трубку 5, в которую из емкости 6 раствор красителя подается открытием краника 7 по трубке 5 во входное сечение трубы 3. Кроме мерного бака 2, для измерения расхода воды, подаваемой по трубам, служит секундомер 8.
Рис. 3.2. Схема экспериментальной установки для иллюстрации ламинарного и турбулентного режимов движения жидкости в круглой трубе
Следовательно, регулирование расхода воды и средней скорости ее движения в трубе 3 и в трубке 5 осуществляется соответственно кранами 4 и 7. На широкой трубе 3 имеются пьезометры 10 (на входе) и 11 (на выходе) для определения потерь напора по длине hl широкой трубы 3 (по разности их показаний). Температура воды в баке 1 измеряется термометром 12. В исходный напорный бак 1 вода подается по питающему трубопроводу 13 открытием вентиля 14 из резервуара лаборатории. Для поддержания уровня воды в баке 1 во время опытов на постоянной отметке имеется переливное устройство (не показано). Уровень воды контролирует электрический уровнемер со световой индикацией (также не показан).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.104.248 (0.333 с.) |
 , (1.1)
, (1.1) (один Паскаль).
(один Паскаль). . (1.2)
. (1.2) . (1.3)
. (1.3)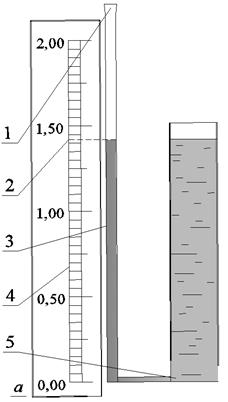


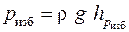 , (1.4)
, (1.4)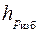 – пьезометрическая высота, т.е. высота, отсчитываемая от точки подключения пьезометра до уровня жидкости в нем.
– пьезометрическая высота, т.е. высота, отсчитываемая от точки подключения пьезометра до уровня жидкости в нем. , (1.5)
, (1.5)
 , (1.6)
, (1.6) , а во втором
, а во втором 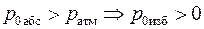 .
.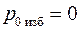 , далее измерить с помощью водомерной трубки 3 со шкалой глубины погружения
, далее измерить с помощью водомерной трубки 3 со шкалой глубины погружения  и
и  точек В и С, а также превышений
точек В и С, а также превышений  и
и  осей вращения стрелок манометров
осей вращения стрелок манометров 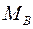 и
и  над точками их подключения. Затем измерить показания всех трех манометров
над точками их подключения. Затем измерить показания всех трех манометров  ,
, 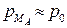






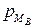

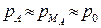









 до значения, указанного преподавателем, после этого компрессор отключить. Далее измерить одновременно показания манометров
до значения, указанного преподавателем, после этого компрессор отключить. Далее измерить одновременно показания манометров 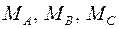 . Результаты измерений записать в графу 5 табл. 1.1. Открыть вентиль 6 для сброса давления сжатого воздуха в атмосферу.
. Результаты измерений записать в графу 5 табл. 1.1. Открыть вентиль 6 для сброса давления сжатого воздуха в атмосферу.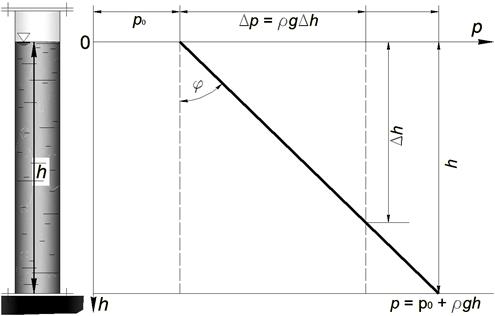
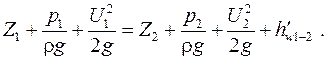 (2.1)
(2.1)
 – гидростатический напор;
– гидростатический напор; – полный напор в рассматриваемом сечении струйки;
– полный напор в рассматриваемом сечении струйки; – потеря полного напора, т.е. часть полного напора, затраченная на преодоление гидравлических сопротивлений на пути между сечениями I – I и II – II.
– потеря полного напора, т.е. часть полного напора, затраченная на преодоление гидравлических сопротивлений на пути между сечениями I – I и II – II. – полная удельная энергия;
– полная удельная энергия;
 .
.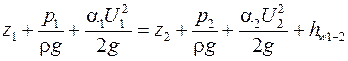 , (2.2)
, (2.2) – скоростной напор, отвечающий средней скорости
– скоростной напор, отвечающий средней скорости  потока жидкости в рассматриваемом живом сечении (здесь Q – расход потока жидкости; w– площадь живого сечения потока);
потока жидкости в рассматриваемом живом сечении (здесь Q – расход потока жидкости; w– площадь живого сечения потока);  по живому сечению потока, обусловленную вязкостью жидкости.
по живому сечению потока, обусловленную вязкостью жидкости.
 f (lg
f (lg  (3.1)
(3.1) , а турбулентный – при Re( d ) > Reкр ( d ).
, а турбулентный – при Re( d ) > Reкр ( d ). (3.2)
(3.2)