
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Приложения производнойСодержание книги Поиск на нашем сайте
Разберите решение задачи 6 данного пособия.
Задача 6. Исследовать функцию
и построить ее график. Решение: Исследование функции проведем по следующей схеме: 1. Найдем область определения функции. 2. Исследуем функцию на непрерывность. 3. Установим, является ли данная функция четной, нечетной. 4. Найдем интервалы возрастания и убывания функции и точки экстремума. 5. Найдем интервалы выпуклости и вогнутости кривой и ее точки перегиба. 6. Найдем асимптоты кривой. Реализуем указанную схему: 1. Функция определена при всех значениях аргумента x, кроме x=1. 2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервалах 3. Для установления четности или нечетности функции проверим выполнимость равенств f(-x)=f(x) (тогда f(x) – четная функция) или f(-x)=-f(x) (тогда f(x) – нечетная функция) для любых x и –x из области определения функции:
следовательно, f(-x) 4. Для исследования функции на экстремум найдем ее первую производную:
Производная Разобьем числовую ось на три интервала (рис. 3): В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает; во втором интервале – положительна и данная функция возрастает. При переходе через точку x=0 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум:
Рис. 3 На рис. 3 знаками +, - указаны интервалы знакопостоянства производной 5. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную:
Вторая производная равна нулю ( Следовательно,
Рис. 4 6. x=1 – точка разрыва функции, причем
Поэтому прямая x=1 является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты
Тогда
При вычислении последнего предела использовалось правило Лопиталя. Значит, прямая y=0 есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 5.
Рис. 5
Вопросы для самопроверки 1. Сформулируйте теоремы Роля, Лагранжа. Каков их геометрический смысл? 2. Какая функция называется возрастающей? Убывающей? 3. Сформулируйте необходимый, достаточный признаки возрастания и убывания функции. 4. Какие точки называются стационарными? Критическими? 5. Назовите достаточные признаки экстремума функции. 6. Какая кривая называется выпуклой? Вогнутой? 7. Как найти интервалы выпуклости и вогнутости кривой? 8. Сформулируйте достаточный признак существования точек перегиба кривой. 9. Что называется асимптотой кривой? Как найти вертикальные и наклонные асимптоты? 10. Назовите схему исследования функции и построения ее графика. 11. В каком случае применяется правило Лопиталя при вычислении пределов?
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.41.200 (0.006 с.) |

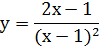
 и
и  . В точке x=1 функция терпит разрыв второго рода.
. В точке x=1 функция терпит разрыв второго рода.
 f(x) и f(-x)
f(x) и f(-x) 
 при x=0 и
при x=0 и  - не существует при x=1. Тем самым имеем две критические точки:
- не существует при x=1. Тем самым имеем две критические точки:  . Но точка
. Но точка  не принадлежит области определения функции, экстремума в ней быть не может.
не принадлежит области определения функции, экстремума в ней быть не может.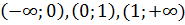 .
.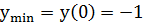 . Значит, точка А(0; -1) – точка минимума функции.
. Значит, точка А(0; -1) – точка минимума функции.

 ) при
) при  и
и  - не существует при x=1. Разобьем числовую ось на три интервала (рис. 4):
- не существует при x=1. Разобьем числовую ось на три интервала (рис. 4): 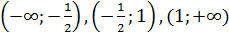 . На правом интервале вторая производная
. На правом интервале вторая производная  , тем самым график является вогнутым. При переходе через точку
, тем самым график является вогнутым. При переходе через точку 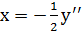 меняет свой знак, поэтому
меняет свой знак, поэтому 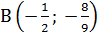 - точка перегиба графика функции.
- точка перегиба графика функции.

 воспользуемся формулами:
воспользуемся формулами:






