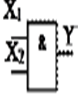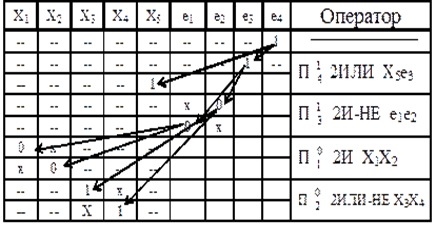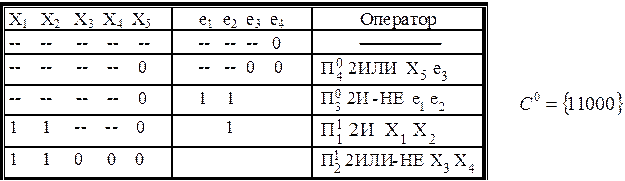Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи анализа и синтеза комбинационных схемСодержание книги
Поиск на нашем сайте
Структурно комбинационная схема может быть представлена как совокупность логических элементов (элементарных логических схем). Логические элементы выполняют над входными переменными элементарные логические операции типа И-НЕ, И, ИЛИ, ИЛИ-НЕ и т.д. Количество входов логического элемента соответствует количеству аргументов воспроизводимой им переключательной функции. Функциональной схемой называют такое графическое изображение комбинационной схемы, при котором: показаны связи между различными элементами; элементы представлены условными обозначениями. Основными характеристиками комбинационных схем являются: сложность; быстродействие. Сложность комбинационной схемы оценивается количеством оборудования, составляющего схему. При разработке схем на основе конкретной элементной базы, количество оборудования обычно измеряется количеством корпусов (модулей) интегральных микросхем, используемых в схеме. В теоретических разработках, ориентируются на произвольную элементную базу, а поэтому для оценки затрат оборудования используется оценка сложности схем по Квайну. Сложность (оценка, цена) по Квайну определяется суммарным количеством входов логических элементов в составе схемы. При данном способе оценки, единицей сложности является один вход логического элемента. Сложность инверсного входа обычно принимается равной двум (если на вход схемы сигналы поступают только в прямой форме). Указанный подход к оценке сложности схем целесообразен по следующим причинам: 1) сложность схемы легко вычисляется по логическим функциям, на основе которых строится схема, например, для ДНФ сложность схемы равна сумме количества букв (при том, что букве со знаком отрицания соответствует сложность два) и количества знаков дизъюнкции (увеличивается на единицу для каждого дизъюнктивного выражения); 2) все классические методы минимизации логических функций обеспечивают минимальность схемы именно в смысле оценки по Квайну; 3) практика показывает, что схема с минимальной оценкой по Квайну обычно реализуется наименьшим количеством конструктивных элементов (корпусов интегральных микросхем). Быстродействие комбинационной схемы оценивается максимальной задержкой сигнала при прохождении сигнала от входа схемы к ее выходу. То есть быстродействие комбинационной схемы определяется промежутком времени от момента поступления входных сигналов до момента установления соответствующих значений выходных сигналов.
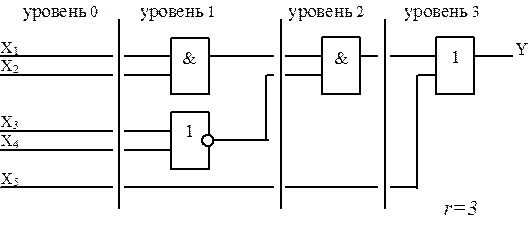
Задержка сигнала кратна числу элементов, через которые проходит сигнал от входа к выходу схемы. Поэтому быстродействие схемы характеризуется значением r*t, где: t является задержкой сигнала на одном элементе; значение r определяется количеством уровней комбинационной схемы, которое рассчитывается приведенным ниже образом. Входам комбинационной схемы приписывается нулевой уровень. Логические элементы, связанные только с входами схемы, относятся к первому уровню. Элемент относится к уровню k, если он связан по входам с элементами уровней k -1, k -2, и т.д. Максимальный уровень элементов r определяет количество уровней комбинационной схемы, называемое рангом схемы. Пример определения ранга r схемы приведен на рисунке 3.
Рисунок 3
Поскольку любая логическая функция может быть представлена в ДНФ, которой соответствует двухуровневая комбинационная схема, то быстродействие любой комбинационной схемы можно довести до 2t. Минимизация переключательной функции с целью уменьшения сложности схем обычно приводит к необходимости представления функций в скобочной форме, которой соответствуют схемы с r > 2. То есть, уменьшение затрат оборудования, в общем случае, приводит к снижению быстродействия схем. В ходе разработки комбинационных схем, приходится решать задачи анализа и синтеза. Задача анализа состоит в определении статических и динамических свойств комбинационной схемы. В статике определяются логические функции, реализуемые комбинационной схемой на основе ее известной структуры. В динамике рассматривается способность надёжного функционирования схемы в переходных процессах при смене значений переменных на ее входах. То есть в динамике определяется наличие на выходах схемы возможных нежелательных импульсных сигналов, которые не следуют непосредственно из выражений для логических функций, реализуемых схемой. Задача синтеза заключается в построении из заданного набора логичес-ких элементов комбинационной схемы, реализующей заданную систему логических функций. Решение задачи синтеза не является однозначным: можно предложить различные варианты комбинационных схем, реализующих одну и ту же систему логических функций, но отличающихся по тем или иным параметрам. Разработчик комбинационных схем выбирает из данного множества вари-антов один, исходя из дополнительных критериев: минимального количества логических элементов, необходимых для реализации схемы; максимального быстродействия и т.д. Существуют различные методы синтеза комбинационных схем, среди которых наиболее разработан канонический метод.
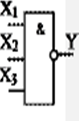
Анализ комбинационных схем Задачи анализа комбинационных схем (КС) возникают при необходи-мости проверить правильность синтеза (на этапе проектирования) или опре-делить логическую функцию, реализуемую КС (при анализе или ремонте схем). Все существующие методы анализа КС делятся на прямые и косвенные. В результате анализа КС прямым методом, получается множество набо-ров входных переменных, обеспечивающих заданное значение на выходе, что позволяет записать логическую функцию, реализуемую схемой, в алгебраи-ческом виде. К прямым методам относится метод p -алгоритмов. Применение косвенных методов позволяет определить реакцию схемы на заданный набор входных переменных в статике или проанализировать пере-ходный процесс смены одного входного набора другим. Примерами косвенных методов анализа являются методы синхронного и асинхронного моделиро-вания. Все упомянутые методы анализа являются машинoориентированными, что позволяет выполнить анализ схемы на компьютере. Для всех методов анализа, необходимо описать схему в виде схемного списка, в который включаются в общем случае следующие данные: номер логического элемента в схеме; логическая функция, реализуемая логическим элементом; входные переменные для данного логического элемента. Например, на рисунке 3.4 представлена схема и список, описывающий ее.
Метод p- алгоритма При анализе комбинационных схем методом p-алгоритма, определяются наборы входных переменных, обеспечивающих заданное значение выходного сигнала КС. Входные наборы, обеспечивающие на выходе КС логический нуль, образуют нулевое покрытие C0. Входные наборы, обеспечивающие на выходе КС логическую единицу, образуют единичное покрытие C1. Рассмотрим покрытия C0 и C1 для простейшего логического элемента 2И, выполняющего функцию Y = X1X2. Таблица истинности для данной функции и условное обозначение элемента 2И приведены на рисунке 3.5.
Как видно из приведенной таблицы, только при единственном наборе X1=1 и X2=1, на выходе логического элемента будет единица. То есть единичное покрытие включает только один набор На выходе логического элемента будет нуль при следующих трех наборах, образующих нулевое покрытие:
Данное покрытие можно упростить, заметив, что первый набор склеивается со вторым и третьим, то есть:
Таким образом, для логического элемента 2И можно утверждать следующее: единица на его выходе будет только при обеих единицах на входах; для обеспечения нуля на выходе, достаточно подать хотя бы на один вход нуль. Рассуждая аналогично, получим таблицу покрытий
Таблица 14
При анализе схемы методом p -алгоритма, задавшись определенным значением сигнала на выходе, заменяют его соответствующим покрытием элемента, формирующего выходной сигнал. В результате, определяется, какие сигналы должны быть на выходах элементов, подключенных к выходному логическому элементу. В свою очередь, сигналы на выходах указанных элементов можно заменить соответствующими покрытиями, то есть определить значения выходных сигналов для других логических элементов, и т.д. Данный процесс продолжается до тех пор, пока не получатся покрытия, состоящие только из входных переменных, называемых опорными. Совокупность таких покрытий и дает соответствующее покрытие схемы. Пример анализа комбинационной схемы, приведенной ранее на рисунке 3.4, методом p-алгоритма представлен в таблицах 15 и 16.
Таблица 15 - Получение единичного покрытия
Таблица 16 – Получение нулевого покрытия
В последних колонках таблиц 15-16 приведен оператор подстановки, в результате работы которого на выходе ЛЭ заменяется соответствующим покрытием. Важно отметить, что все значения переменных, записанные в одной строке, должны одновременно быть в наличии для обеспечения заданного значения выходного сигнала. Поэтому, при замене одного из значений в строке соответствующим покрытием, все остальные значения для других переменных в этой строке должны присутствовать совместно с данным покрытием. На основании полученного единичного покрытия, можно записать логическую функцию, реализуемую схемой:
В дальнейшем можно сравнить полученную логическую функцию с той, по которой строилась схема, и проверить правильность ее построения. При анализе схемы может оказаться, что некоторая переменная, получившая на одном из предыдущих шагов некоторые значения, на данном шаге должна принять противоположное значение. Возникшее противоречие говорит о том, что данный путь является тупиковым, и его необходимо исключить из дальнейшего рассмотрения. Если ни при одной комбинации входных переменных не обеспечивается значение 1 (0) на выходе, то схема реализует константу 0 (1) соответственно.
2 КОНТРОЛЬНІ ПИТАННЯ 1. Скласти таблиці переходів RS -, R -, S -, Е -, D -, Т -; DV - і JK- тригерів. 2. Назвати відмінності між синхронними й асинхронними тригерами. 3. У чому полягають розходження між тригерами, керованими рівнем тактуючого сигналу, та тригерами з внутрішньою затримкою, в яких випадках використовуються зазначені типи тригерів? 4. Пояснити роботу синхронних тригерів, виконаних по МS-схемі, за схемою трьох тригерів із ЗЕ на вентилях I-АБО-НІ. 5. Укажіть розходження між синхронними й асинхронними входами синхронного тригеру. 6. Пояснити, як будується часова діаграма роботи тригеру. 7. Охарактеризувати етапи проектування тригерних схем i побудувати тригери за заданою таблицею переходів. 8. Назвати основні часові характеристики тригерів. 9. Порівняти щодо швидкодії тригери з внутрішньою затримкою, виконані за різними схемами та сформулювати, які часові умови є основними для правильної роботи таких тригерів? 10. Як перейти до базису І-НІ і АБО-НІ, якщо функцію представлено в МДНФ? 11. Як побудувати T-тригер на основі RS-, D- і JK-тригерів? 12. Які зміни необхідно здійснити в схемі тригеру з внутрішньою затримкою, щоб змінити фронт тактуючого сигналу, за яким здійснюється переключення тригеру? 13. Чи можна замінити в цифровому пристрої синхронний JK-тригер на інший синхронний тригер, не порушуючи правильності його роботи? 14. Охарактеризувати в цiлому питання про аналiз логiчних схем i динамiчних процесiв у цифрових автоматах. 15. Назвати основнi типи цифрових автоматiв; 16. У чому полягають задачi аналiзу та синтезу комбiнацiйних схем? 17. Охарактеризувати методи аналiзу комбiнацiйних схем. 18. Сформулювати суть методу p-алгоритму.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 3960; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.186.56 (0.011 с.) |



 ={1 1}.
={1 1}.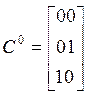 .
.
 и
и  для основных логических элементов, представленных ниже в таблице 14.
для основных логических элементов, представленных ниже в таблице 14.