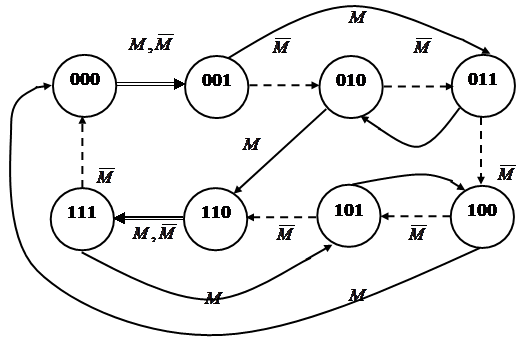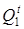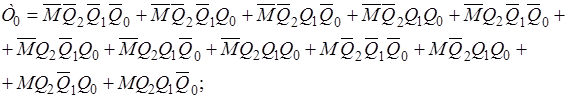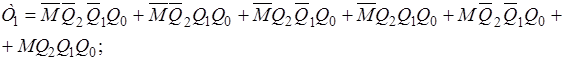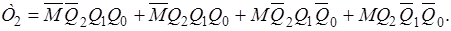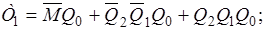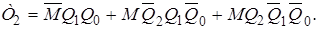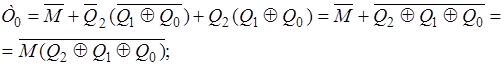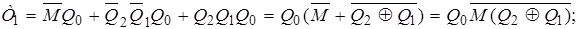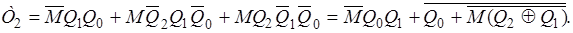Приклад синтезу послідовністного цифрового автомату

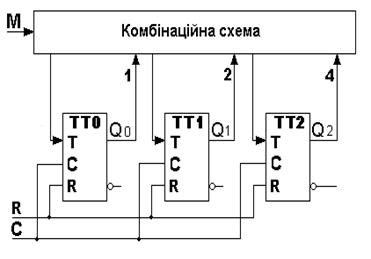
Постановка завдання (вихідне завдання функціонування): необхідно синтезувати трирозрядний додаючий двійковий лічильник на основі Т -тригерів, алгоритм функціонування якого визначає керуючий сигнал М: якщо М = 0, то лічильник працює як звичайний лічильник прямого рахування; якщо М = 1, то лічильник працює в коді Грея; зміна керуючого сигналу М веде до зміни режиму роботи (наступний стан лічильника буде належати вже іншому коду).

Синтез проведемо без обмежень на використовуваний логічний базис iз метою отримання схеми з мінімальною кількістю елементів.

На основі опису ЦА, можливо відразу отримати його структурну схему, зображену на рисунку 1.21.

 

Рисунок 1.21 - Структурна схема ЦА

Комбінаційна схема реалізує необхідні функції збудження Т -тригерів на основі їх станів i керуючого сигналу М. Усі тригери мають загальні входи скидання та синхронізації.

Етап 1. Формалізоване задавання функціонування. Мінімізація та кодування станів автомату. Алгоритм функціонування лічильнику в обох заданих режимах може бути поданий таблицею 10. На підставі таблицi 10 складемо граф переходів (діаграму станів) лічильнику (рисунок 1.22).

Напрямки переходів на діаграмі вказані: для рахування в коді 8421 – пунктирними лініями, для рахування в коді Грея – суцільними лініями. Ділянки діаграми, де напрямки переходів у двох режимах співпадають, вказано подвійними лініями.

Таблиця 10

Такт	М=0; код 8421	М=1; код Грея
Х2	Х1	Х0	Х2	Х1	Х0
Початковий стан

 

 

 

Рисунок 1.22 - Діаграма станів лічильника

Етап 2.Складання таблиці переходів автомату. На підставі діаграми станів, iз урахуванням алгоритму функціонування Т -тригеру, складаємо таблицю переходів ЦА (таблиця 11).

 

Таблиця 11

М	Початковий Стан	Наступний стан	Сигнали на входах тригерів
						Т2	Т1	Т0

Етап 3. Отримання функцій збудження тригерів ЦА (у вигляді ДДНФ).

Етап 4.Мінімізація функції збудження тригерів. Перший етап мінімізації функцій збудження Т -тригерів виконаємо з застосуванням карт Карно (рисунок 1.23).

 

	Q 2 Q 2   M         M         Q 0         Q 0           Q 1 Q 1		Q 2 Q 2   M         M         Q 0         Q 0           Q 1 Q 1
		Т0		Т1

 

 

Рисунок 1.23 - Мінімізація функцій збудження тригерів

за допомогою карт Карно (початок)

 

	Q 2	Q 2
M
M					Q 0
					Q 0
		Q 1	Q 1

 

 

	Т2

 

Рисунок 1.23 - Мінімізація функцій збудження тригерів

за допомогою карт Карно (продовження)

Отримаємо функції збудження тригерів у вигляді МДНФ:

Використовуючи відомі співвідношення (розподільний закон, правила де Моргана тощо), остаточно отримаємо:

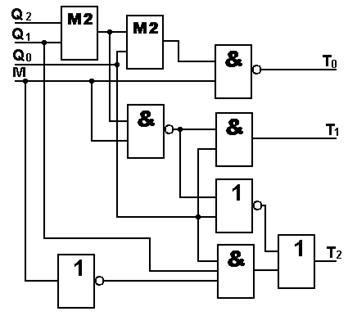
Етап 5. Складання логічної схеми цифрового автомату. Логічну схему комбінаційної частини ЦА, що формує необхідні функції збудження тригерів, подано на рисунку 1.24.

 

 

Рисунок 1.24 - Схема комбінаційної частини ЦА