
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действительный процесс расширения пара в соплах и на рабочих лопатках.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Действительный процесс течения рабочей среды в каналах турбинных решеток отличается от изоэнтропийного тем, что протекает с внутренним (подвод теплоты трения), а в общем случае — и с внешним (передача теплоты окружающей среде или охлаждающему телу) теплообменом. Из-за наличия теплообмена энтропия рабочей среды не остается постоянной, а возрастает при подводе теплоты трения и уменьшается при отводе теплоты в окружающую среду или передаче ее охлаждающему телу (газовые турбины). В частном случае, когда подводимая теплота равна отводимой, энтропия сохранится неизменной, однако сам процесс остается необратимым и отличается от ранее рассмотренного обратимого изоэнтропийного процесса. Причинами внутреннего теплообмена являются различные потери, имеющие место в реальном процессе расширения, такие, как трение рабочей среды о стенки каналов, вихреобразования и др. Отмеченные потери приводят к тому, что часть кинетической энергии в процессе расширения преобразуется в тепловую, которая возвращается к рабочей среде. В результате этого энтальпия рабочей среды в конце действительного процесса расширения больше, чем в конце изоэнтропийного, а действительная скорость истечения меньше, чем теоретическая скорость c1t. Построим процесс расширения пара в соплах. Если пар входит в сопла с начальными параметрами р0, t0 и скоростью с0, то начальное состояние пара на і — s диаграмме (рис. 12.4) определится пересечением изобары р0 с изотермой t0 (точка А0 ). Процесс изоэнтропийного торможения потока пара изобразится на диаграмме вертикальной линией А0А0 *, т. е. параметры торможения характеризуются точкой А0 * .
Рис. 12.4. Изоэнтропийный и действительный процессы расширения пара в соплах на i - s диаграмме Состояние пара на выходе из сопл при изоэнтропийном расширении определяется пересечением вертикальной линии, проведенной из точки А0, и изобары р1 (точка А1t). На диаграмме отрезок А0 А1t и, равный hac = i0 – i1t называется изоэнтропийным перепадом энтальпий, а отрезок А0 * А1t, равный hac *= i0 * – i1t, называется располагаемым изоэнтропийным перепадом энтальпий.
Кинетическая энергия потока в сопле может быть выражена через перепад энтальпий: c21t /2 = i0 * – i1t = hac * Пар, расширяясь в соплах, преодолевает ряд сопротивлений, на что затрачивается часть кинетической энергии, приобретенной им. Поэтому действительная скорость с1 выхода пара из сопла меньше теоретической с1t. Это уменьшение скорости можно учесть с помощью коэффициента скорости сопла φ (фи), который представляет собой отношение действительной скорости за соплом к теоретической (φ = с1/с1t).
Используя формулу (12.6):
и введя в нее коэффициент скорости n, получаем формулу действительной скорости истечения из сопл:
Кинетическая энергия пара, затраченная на преодоление вредных сопротивлений, преобразуется в тепловую, вследствие чего энтальпия пара массой 1кг в выходном сечении сопла при том же давлении будет немного больше той, которую он имел бы при изоэнтропийном расширении i1 > i1t. Повышение энтальпии (i1 - i1t) эквивалентно потере кинетической энергии в соплах, выраженной в тепловых единицах, и носит название потери в соплах qc. Если значение скоростного коэффициента n для данного сопла известно, то легко найти потерю в соплах:
q c = c21t/2 – c21/2 = (c21t - φ c21t)/2 = (1 - φ2) c21t/2
где: c21t/2 — кинетическая энергия при изоэнтропийном процессе расширения; c21/2 — кинетическая энергия при действительном процессе расширения. Учитывая, что c21t/2 = h ac*, поэтому:
q c = (1 - φ2) h ac* = ξ с h ac (12.11)
где: ξ с — (кси) коэффициент потерь энергии в соплах.
Потери при расширении пара в соплах (потери в сопловых решетках) у современных турбин невелики φ = 0,94 - 0,98 и соответственно ξ с = 5 - 15%.
Потери в суживающихся соплах обычно меньше, чем в расширяющихся, поэтому в паровых турбинах обычно устанавливают суживающиеся сопла, у которых скорости истечения пара меньше критической. Потери в соплах, а следовательно, коэффициент скорости зависят от качества поверхности сопл, поэтому поверхности сопл полируют, и при ремонтах очищают от отложений. Процесс действительного расширения пара или газа в соплах изобразится в i - s диаграмме не изоэнтропой А0 А1t а некоторой политропой А0 А1 (см. рис. 12.4). Точку А1, характеризующую состояние пара при выходе из сопл, находят следующим образом. По изоэнтропе от точки А1t вверх откладывают потерю в соплах q c = i 1 - i 1t. Получив точку В1, проводят через нее горизонталь до пересечения с изобарой конечного давления р1 и находят точку А1. Обычно кривую процесса — политропу А0 А1 приближенно вычерчивают как прямую, соединяя точки А0 и А1. Действительный процесс расширения в сопловых и рабочих каналах турбинной ступени без внешнего теплообмена (а именно такой в дальнейшем будет рассматриваться) изображается в диаграмме i—s наклонными линиями 0—1 и 1—2, соединяющими точки начала и конца действительного процесса течения (рис. 4.9). Линии 0—1 и 1 — 2 будем в дальнейшем условно называть политропами расширения.
Рис. 4.9 Действительный процесс расширения в сопловой и рабочей решетках в диаграмме i — s Используя формулы изоэнтропийного процесса расширения и вводя в них коэффициент скорости рабочей решетки ψ (пси), получаем формулу для действительной скорости истечения из рабочей решетки (рис. 4.9):
Где: ψ = w2/w2t — коэффициент скорости рабочей решетки.
Коэффициенты φ и ψ, входящие в уравнения скоростей с1 и w12, определяют опытным путем. Они зависят от конфигурации профиля лопатки, геометрических размеров решеток и других факторов. Средние значения коэффициента (пси) ψ = 0,90 - 0,96.
Так как действительная скорость w2 истечения из рабочих лопаток меньше теоретической w2t, разность кинетических энергий потока при изоэнтропийном и действительном процессах расширения представляет собой потерю кинетической энергии газа в действительном процессе расширения. Обозначая потерю на рабочих лопатках через qр получим:
Потерянная кинетическая энергия qс и qр, эквивалентная работе сил трения, превращается в тепловую и передается в пределах канала потоку. В результате энтальпия і1 потока в конце действительного процесса расширения в соплах (в точке 1 на рис. 4.9) и энтальпия i2 в конце действительного процесса расширения на рабочих лопатках (в точке 2) будут больше соответствующих энтальпий i1t и i2i конца изоэнтропийного процесса расширения (точки 1t и 2t). Очевидно, что і1 = i1t + qс и i2 = i2t + qр
Отсюда следует, что для построения действительного процесса расширения в соплах в диаграмме i—s необходимо от точки 1t конца изоэнтропийного процесса расширения отложить вверх по изоэнтропе потерю qH и найти точку 1 пересечения энтальпии і1 с изобарой р1. Прямая 0 — 1 условно будет представлять политропу расширения в сопловой решетке. Аналогично строится политропа расширения 1—2 в рабочей решетке.
Отношение потерянной в решетке кинетической энергии к располагаемой энергии решетки, равной полному изоэнтропийному теплоперепаду, называется коэффициентом потерь решетки ξ р (кси). Обозначая коэффициент потерь в рабочей решетке через ξ р (кси) и учитывая выражение (4.49), получим:
ξ р = qр / h aр* = 1 – ψ2
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


 (12.6)
(12.6)


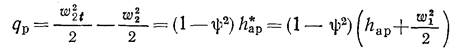 (4.49)
(4.49)


