Несимметричное обтекание конуса
Сверхзвуковым потоком
При сверхзвуковом обтекании конуса под углом атаки  поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры газа в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры газа в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат  (рис. 9.5), выбранной таким образом, что координате (рис. 9.5), выбранной таким образом, что координате  соответствует вершина конуса, оси координат соответствует вершина конуса, оси координат  (ось 3) – направление скорости набегающего потока, а меридиональной плоскости (ось 3) – направление скорости набегающего потока, а меридиональной плоскости 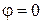 – плоскость, проходящая через ось 3 и ось 1, т. е. ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом – плоскость, проходящая через ось 3 и ось 1, т. е. ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом  (на рис. 9.5 этот угол отрицательный), будет следующим: (на рис. 9.5 этот угол отрицательный), будет следующим:
 , (9.8) , (9.8)
где  – сферическая координата для образующей конуса. Для подветренной образующей – сферическая координата для образующей конуса. Для подветренной образующей 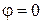 , а для наветренной – , а для наветренной – 
| | | | Рис. 9.5. Схема потока около конуса,
наклоненного под углом атаки:
1 – ось конуса; 2 – ось скачка уплотнения; 3 – ось координат и направление 
| |
Из свойств конического потока следует, что значения его параметров не зависят от r, а являются функциями переменных  и и  . Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости . Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости  будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок одинаковы для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок одинаковы для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости  . Однако в связи с тем, что угол наклона скачка . Однако в связи с тем, что угол наклона скачка  неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла  . Из этого следует, что в целом несимметричный конический поток за скачком оказывается неизоэнтропическим. . Из этого следует, что в целом несимметричный конический поток за скачком оказывается неизоэнтропическим.
Теоретической основой для исследования такого потока являются уравнения движения идеальной среды и уравнение неразрывности в сферической системе координат. Решения системы дифференциальных уравнений находят в виде
 (9.9) (9.9)
Аналогичные выражения записывают и для остальных искомых параметров: составляющих скорости по соответствующим направлениям сферической системы координат  и и  , давления , давления  , плотности , плотности  , где , где  – это параметры симметричного обтекания на конусе с углом – это параметры симметричного обтекания на конусе с углом  . .
Каждое из уравнений (9.9) представляет собой ряд, в котором член, линейный по отношению к углу атаки, определяет решение в первом приближении, а квадратичный член – во втором. При малых углах  значения параметров будут мало отличаться от соответствующих значений при симметричном обтекании, и влияние угла значения параметров будут мало отличаться от соответствующих значений при симметричном обтекании, и влияние угла  достаточно учесть только линейными членами. С возрастанием достаточно учесть только линейными членами. С возрастанием  возникает необходимость вести расчет с учетом второго приближения, которым обычно и ограничиваются, полагая, что углы атаки невелики (что справедливо для баллистических ракет и ракет-носителей). возникает необходимость вести расчет с учетом второго приближения, которым обычно и ограничиваются, полагая, что углы атаки невелики (что справедливо для баллистических ракет и ракет-носителей).
Из выражений (9.9) следует, что определение параметров обтекания конуса под углом атаки начинается с решения частной задачи о симметричном потоке около того же конуса. В результате ее решения отыскиваются значения  в зависимости от угла в зависимости от угла  . Далее рассматривается влияние угла атаки. . Далее рассматривается влияние угла атаки.
Задача о влиянии угла атаки в первом приближении сводится к определению коэффициентов 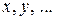 рядов (9.9) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (9.9) запишется следующим образом: рядов (9.9) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (9.9) запишется следующим образом:
 (9.10) (9.10)
В рассматриваемых уравнениях коэффициенты  можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты  и другие – во втором. Все эти коэффициенты зависят от одной переменной и другие – во втором. Все эти коэффициенты зависят от одной переменной  . .
Найденные в результате решения задачи коэффициенты x, y, z, отнесенные к максимальной скорости  , а также безразмерные величины , а также безразмерные величины  просчитаны для различных углов конуса и чисел просчитаны для различных углов конуса и чисел  и внесены в таблицы. При их помощи по формулам (9.10) ведется расчет скорости, давления и плотности численными методами (в аэродинамике наиболее развиты конечно-разностные методы) с помощью ЭВМ. Не вдаваясь в подробности расчетов, рассмотрим их результаты (рис. 9.6). и внесены в таблицы. При их помощи по формулам (9.10) ведется расчет скорости, давления и плотности численными методами (в аэродинамике наиболее развиты конечно-разностные методы) с помощью ЭВМ. Не вдаваясь в подробности расчетов, рассмотрим их результаты (рис. 9.6).

Рис. 9.6. Зависимости коэффициента давления:
а – от угла атаки; б – от угла ψ; в – от числа Маха
Простой логический анализ течения около конуса позволяет сделать вывод, что на его наветренной стороне ( ) давление должно быть больше, чем на подветренной. Это наглядно иллюстрируют приведенные качественные зависимости. С увеличением угла конуса давление возрастает на всей его поверхности. При малых углах атаки ) давление должно быть больше, чем на подветренной. Это наглядно иллюстрируют приведенные качественные зависимости. С увеличением угла конуса давление возрастает на всей его поверхности. При малых углах атаки  коэффициент давления коэффициент давления  практически линейно зависит от практически линейно зависит от  (рис. 9.6, а). С увеличением числа Маха набегающего потока (рис. 9.6, в) коэффициент давления монотонно уменьшается во всех меридиональных плоскостях. (рис. 9.6, а). С увеличением числа Маха набегающего потока (рис. 9.6, в) коэффициент давления монотонно уменьшается во всех меридиональных плоскостях.
Приближенный метод расчета.
Метод касательных конусов
Для приближенного расчета давления и коэффициента волнового сопротивления заостренных тел вращения произвольной формы применяется метод касательных (местных) конусов (рис. 9.7).
Согласно этому методу, коэффициент давления в каждой точке тела с криволинейной образующей принимается равным коэффициенту давления на местном конусе с углом полураствора  (при том же числе Маха). Образующей местного конуса является касательная к поверхности тела в данной точке, а осью конуса – ось потока, т. е. направление вектора скорости (при том же числе Маха). Образующей местного конуса является касательная к поверхности тела в данной точке, а осью конуса – ось потока, т. е. направление вектора скорости  (если угол атаки (если угол атаки  ) или продольная ось тела (при симметричном обтекании). То есть производят замену плавной образующей тела вращения на ломаную линию (исходное тело с криволинейной образующей заменяют составным коническим). Таким образом, можно приближенно определить закон распределения давления по телу вращения и рассчитать течение во всей области между скачком и телом. ) или продольная ось тела (при симметричном обтекании). То есть производят замену плавной образующей тела вращения на ломаную линию (исходное тело с криволинейной образующей заменяют составным коническим). Таким образом, можно приближенно определить закон распределения давления по телу вращения и рассчитать течение во всей области между скачком и телом.
 В случае аналитического задания формы тела определение угла местного конуса (угла наклона касательной) выполняется достаточно просто. Например, для носовой части, форма которой получена вращением дуги окружности радиуса В случае аналитического задания формы тела определение угла местного конуса (угла наклона касательной) выполняется достаточно просто. Например, для носовой части, форма которой получена вращением дуги окружности радиуса  вокруг некоторой оси, угол наклона касательной в точке с местным радиусом тела вращения вокруг некоторой оси, угол наклона касательной в точке с местным радиусом тела вращения  определяется по следующей формуле: определяется по следующей формуле:  , где , где  – радиус миделя (наибольшего поперечного сечения тела). – радиус миделя (наибольшего поперечного сечения тела).
 Аналогично, для оценки параметров на поверхности конуса при Аналогично, для оценки параметров на поверхности конуса при  можно воспользоваться результатами, полученными для можно воспользоваться результатами, полученными для  . Приближенные результаты можно получить, применив и для этого случая метод местных конусов (рис. 9.8). . Приближенные результаты можно получить, применив и для этого случая метод местных конусов (рис. 9.8).
В приложении к несимметричному обтеканию конуса делается предположение, что каждая образующая конуса, отклоненного на угол  , принадлежит условному конусу с углом , принадлежит условному конусу с углом  (местный угол), симметрично обтекаемому потоком ( (местный угол), симметрично обтекаемому потоком ( – подветренная образующая; – подветренная образующая; 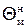 – наветренная). Имея результаты теории симметричного обтекания, можно определить параметры на той образующей, которая принадлежит этому «местному» конусу. Таким образом, основным элементом расчета является угол «местного конуса». – наветренная). Имея результаты теории симметричного обтекания, можно определить параметры на той образующей, которая принадлежит этому «местному» конусу. Таким образом, основным элементом расчета является угол «местного конуса».
Величину угла  можно рассчитать по формуле (9.8) или по приближенной формуле, применимой для малых углов можно рассчитать по формуле (9.8) или по приближенной формуле, применимой для малых углов  : :
 . (9.11) . (9.11)
В формуле (9.11)  отсчитывают от оси конуса, а угол отсчитывают от оси конуса, а угол  в формуле (9.8) – от вектора в формуле (9.8) – от вектора  (см. рис. 9.5). За начало отсчета обоих углов принято направление на подветренную образующую конуса, лежащую в плоскости симметрии течения (в плоскости «вектор скорости – ось конуса»). (см. рис. 9.5). За начало отсчета обоих углов принято направление на подветренную образующую конуса, лежащую в плоскости симметрии течения (в плоскости «вектор скорости – ось конуса»).
Чем больше скорость набегающего потока и меньше угол атаки, тем меньше погрешность расчетов по этому методу. Поэтому его целесообразно применять при малых углах  и больших числах и больших числах  . .
|



 поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры газа в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат
поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры газа в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат  (рис. 9.5), выбранной таким образом, что координате
(рис. 9.5), выбранной таким образом, что координате  соответствует вершина конуса, оси координат
соответствует вершина конуса, оси координат  (ось 3) – направление скорости набегающего потока, а меридиональной плоскости
(ось 3) – направление скорости набегающего потока, а меридиональной плоскости 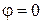 – плоскость, проходящая через ось 3 и ось 1, т. е. ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом
– плоскость, проходящая через ось 3 и ось 1, т. е. ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом  (на рис. 9.5 этот угол отрицательный), будет следующим:
(на рис. 9.5 этот угол отрицательный), будет следующим: , (9.8)
, (9.8) – сферическая координата для образующей конуса. Для подветренной образующей
– сферическая координата для образующей конуса. Для подветренной образующей 


 . Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости
. Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости  будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок одинаковы для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости
будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок одинаковы для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости  неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла
неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла  (9.9)
(9.9) и
и  , давления
, давления  , плотности
, плотности  , где
, где  – это параметры симметричного обтекания на конусе с углом
– это параметры симметричного обтекания на конусе с углом  в зависимости от угла
в зависимости от угла 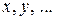 рядов (9.9) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (9.9) запишется следующим образом:
рядов (9.9) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (9.9) запишется следующим образом: (9.10)
(9.10) можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты
можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты  и другие – во втором. Все эти коэффициенты зависят от одной переменной
и другие – во втором. Все эти коэффициенты зависят от одной переменной  , а также безразмерные величины
, а также безразмерные величины  просчитаны для различных углов конуса и чисел
просчитаны для различных углов конуса и чисел  и внесены в таблицы. При их помощи по формулам (9.10) ведется расчет скорости, давления и плотности численными методами (в аэродинамике наиболее развиты конечно-разностные методы) с помощью ЭВМ. Не вдаваясь в подробности расчетов, рассмотрим их результаты (рис. 9.6).
и внесены в таблицы. При их помощи по формулам (9.10) ведется расчет скорости, давления и плотности численными методами (в аэродинамике наиболее развиты конечно-разностные методы) с помощью ЭВМ. Не вдаваясь в подробности расчетов, рассмотрим их результаты (рис. 9.6).
 ) давление должно быть больше, чем на подветренной. Это наглядно иллюстрируют приведенные качественные зависимости. С увеличением угла конуса давление возрастает на всей его поверхности. При малых углах атаки
) давление должно быть больше, чем на подветренной. Это наглядно иллюстрируют приведенные качественные зависимости. С увеличением угла конуса давление возрастает на всей его поверхности. При малых углах атаки  коэффициент давления
коэффициент давления  практически линейно зависит от
практически линейно зависит от  (при том же числе Маха). Образующей местного конуса является касательная к поверхности тела в данной точке, а осью конуса – ось потока, т. е. направление вектора скорости
(при том же числе Маха). Образующей местного конуса является касательная к поверхности тела в данной точке, а осью конуса – ось потока, т. е. направление вектора скорости  (если угол атаки
(если угол атаки  В случае аналитического задания формы тела определение угла местного конуса (угла наклона касательной) выполняется достаточно просто. Например, для носовой части, форма которой получена вращением дуги окружности радиуса
В случае аналитического задания формы тела определение угла местного конуса (угла наклона касательной) выполняется достаточно просто. Например, для носовой части, форма которой получена вращением дуги окружности радиуса  вокруг некоторой оси, угол наклона касательной в точке с местным радиусом тела вращения
вокруг некоторой оси, угол наклона касательной в точке с местным радиусом тела вращения  определяется по следующей формуле:
определяется по следующей формуле:  , где
, где  – радиус миделя (наибольшего поперечного сечения тела).
– радиус миделя (наибольшего поперечного сечения тела). Аналогично, для оценки параметров на поверхности конуса при
Аналогично, для оценки параметров на поверхности конуса при  . Приближенные результаты можно получить, применив и для этого случая метод местных конусов (рис. 9.8).
. Приближенные результаты можно получить, применив и для этого случая метод местных конусов (рис. 9.8). (местный угол), симметрично обтекаемому потоком (
(местный угол), симметрично обтекаемому потоком ( – подветренная образующая;
– подветренная образующая; 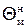 – наветренная). Имея результаты теории симметричного обтекания, можно определить параметры на той образующей, которая принадлежит этому «местному» конусу. Таким образом, основным элементом расчета является угол «местного конуса».
– наветренная). Имея результаты теории симметричного обтекания, можно определить параметры на той образующей, которая принадлежит этому «местному» конусу. Таким образом, основным элементом расчета является угол «местного конуса». . (9.11)
. (9.11) отсчитывают от оси конуса, а угол
отсчитывают от оси конуса, а угол 


