
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение нормальной и продольной силы
По распределению давления
Получим формулы для определения нормальной и продольной силы, а также момента тангажа относительно вершины для конуса, обтекаемого идеальной жидкостью. В этом случае на поверхность тела действуют только силы аэродинамического давления. Выделим на поверхности тела элементарную площадку:
Рис. 9.9. Определение нормальной и продольной силы
Так как
Коэффициент нормальной силы равен
Аналогично получим формулу для коэффициента продольной силы. Элементарная продольная сила равна
Формулы (9.12) и (9.13) применимы для любого тела вращения. Для конуса
Коэффициент давления Анализ результатов экспериментов и расчетов для конусов показывает, что при увеличении Нормальная сила и момент тангажа Для тонких тел вращения
Рассмотрим обтекание тонкого удлиненного тела вращения при малом угле атаке. В этом случае возмущенный поток в окрестности тела мало отличается от невозмущенного. По методу малых возмущений потенциал скорости потока удовлетворяет линейному дифференциальному уравнению и может быть представлен в виде суммы трех составляющих (рис. 9.10):
где
Согласно линейной теории потенциал обтекания тонкого тела при сверхзвуковых скоростях описывается уравнением
а б в
Рис. 9.10. Тонкое тело вращения при малом угле атаки: а –
В безразмерных координатах (
Для тонких тел
Уравнение (9.17) есть ни что иное, как уравнение Лапласа – уравнение неразрывности для плоского потенциального течения несжимаемой жидкости. То есть поток в плоскости ZOY поперечного сечения тонкого тела можно считать двумерным, совпадающим с поперечным обтеканием цилиндра радиусом, равным местному радиусу тела вращения В результате некоторых преобразований уравнения (9.17) и интегрирования по углу
где
а б
Рис. 9.11. Распределение нормальной силы по поверхности конуса: а – цилиндрического тела; б – параболического тела
Носовая часть корпуса Нормальная суммарная сила для тонкого тела вращения равна
а коэффициент нормальной силы равен
где
Коэффициент момента равен
т. е.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.129.19 (0.014 с.) |
 (рис. 9.9). Нормальная сила, действующая на эту площадку, равна
(рис. 9.9). Нормальная сила, действующая на эту площадку, равна .
.

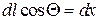 , после интегрирования в пределах
, после интегрирования в пределах 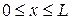
 (
( – длина тела вращения) и
– длина тела вращения) и 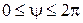 получим выражение для нормальной силы, действующей на всю поверхность тела:
получим выражение для нормальной силы, действующей на всю поверхность тела: .
.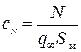 , где
, где  – площадь миделевого сечения тела. Перейдем к безразмерным величинам и сделаем следующие замены:
– площадь миделевого сечения тела. Перейдем к безразмерным величинам и сделаем следующие замены:  ,
,  ,
, 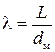 (
( – удлинение тела;
– удлинение тела;  – диаметр миделя). Тогда выражение для коэффициента нормальной силы примет вид
– диаметр миделя). Тогда выражение для коэффициента нормальной силы примет вид ,
, . (9.12)
. (9.12) . Так как
. Так как  , то
, то и
и  . (9.13)
. (9.13)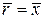 ,
, 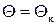 и
и  . Тогда из формул (9.12) и (9.13) получим следующее:
. Тогда из формул (9.12) и (9.13) получим следующее: , (9.14)
, (9.14) . (9.15)
. (9.15) . Коэффициент момента относительно вершины конуса, отнесенный к длине конуса
. Коэффициент момента относительно вершины конуса, отнесенный к длине конуса  равен
равен  . Из формул (9.14) и (9.15) следует, что коэффициенты
. Из формул (9.14) и (9.15) следует, что коэффициенты  и
и  зависят от углов атаки
зависят от углов атаки  , полураствора конуса
, полураствора конуса  и числа Маха
и числа Маха  , т. е.
, т. е.  .
. увеличивается, а
увеличивается, а  ,
, потенциал невозмущенного потока;
потенциал невозмущенного потока;  – потенциал скорости возмущения при осесимметричном
– потенциал скорости возмущения при осесимметричном  обтекании тела потоком со скоростью
обтекании тела потоком со скоростью 
 – потенциал, возникающий при поперечном обтекании тела потоком со скоростью
– потенциал, возникающий при поперечном обтекании тела потоком со скоростью  .
. .
.
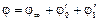 ; б –
; б –  в –
в – 
 и
и  , где
, где  – диаметр миделевого сечения;
– диаметр миделевого сечения;  . (9.16)
. (9.16)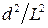 << 1, и, пренебрегая первым слагаемым в выражении (9.16) ввиду его малости, запишем следующее:
<< 1, и, пренебрегая первым слагаемым в выражении (9.16) ввиду его малости, запишем следующее: . (9.17)
. (9.17) , несжимаемой жидкостью. Кроме того, из уравнения (9.17) следует также, что потенциал обтекания тонкого тела не зависит от числа
, несжимаемой жидкостью. Кроме того, из уравнения (9.17) следует также, что потенциал обтекания тонкого тела не зависит от числа  получим выражение для нормальной силы, действующей на элемент тела вращения длиной
получим выражение для нормальной силы, действующей на элемент тела вращения длиной  :
: , (9.18)
, (9.18) . Отсюда следует, что нормальная сила
. Отсюда следует, что нормальная сила  появляется только на участках с переменной площадью поперечного сечения. Знак силы зависит от знака производной
появляется только на участках с переменной площадью поперечного сечения. Знак силы зависит от знака производной  (рис. 9.11).
(рис. 9.11).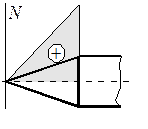

 создает положительную нормальную силу, а суживающаяся хвостовая часть
создает положительную нормальную силу, а суживающаяся хвостовая часть  – отрицательную нормальную силу, тогда как цилиндрический отсек, для которого
– отрицательную нормальную силу, тогда как цилиндрический отсек, для которого 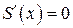 , при обтекании тела идеальной жидкостью не создает нормальной силы.
, при обтекании тела идеальной жидкостью не создает нормальной силы.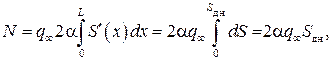
 , (9.19)
, (9.19) – относительная площадь донного среза (угол
– относительная площадь донного среза (угол 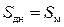 и
и  независимо от формы носовой части и числа Маха.
независимо от формы носовой части и числа Маха. Момент элементарной нормальной силы относительно вершины тела (рис. 9.12) – момент тангажа – равен
Момент элементарной нормальной силы относительно вершины тела (рис. 9.12) – момент тангажа – равен  Знак «минус» в этой формуле говорит о том, что создаваемый момент – это момент на пикирование:
Знак «минус» в этой формуле говорит о том, что создаваемый момент – это момент на пикирование: ,
,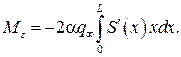
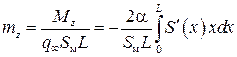 ,
,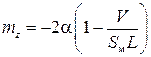 , где
, где  – объем носовой части.
– объем носовой части.


