Осесимметричное обтекание острого конуса
Глава 9
ОБТЕКАНИЕ ТЕЛ ВРАЩЕНИЯ
СВЕРХЗВУКОВЫМ ПОТОКОМ
Коническим называют поток, в котором параметры газа на конической поверхности сохраняются постоянными. Они изменяются только при переходе с одной конической поверхности на другую.
Осесимметричным называют течение, обладающее симметрией относительно оси тела. В этом случае течение газа во всех меридиональных плоскостях одинаково, и движение газа можно изучать как плоское в одной из меридиональных плоскостей.
Несимметричное обтекание конуса
Сверхзвуковым потоком
При сверхзвуковом обтекании конуса под углом атаки  поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры газа в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры газа в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат  (рис. 9.5), выбранной таким образом, что координате (рис. 9.5), выбранной таким образом, что координате  соответствует вершина конуса, оси координат соответствует вершина конуса, оси координат  (ось 3) – направление скорости набегающего потока, а меридиональной плоскости (ось 3) – направление скорости набегающего потока, а меридиональной плоскости 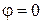 – плоскость, проходящая через ось 3 и ось 1, т. е. ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом – плоскость, проходящая через ось 3 и ось 1, т. е. ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом  (на рис. 9.5 этот угол отрицательный), будет следующим: (на рис. 9.5 этот угол отрицательный), будет следующим:
 , (9.8) , (9.8)
где  – сферическая координата для образующей конуса. Для подветренной образующей – сферическая координата для образующей конуса. Для подветренной образующей 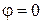 , а для наветренной – , а для наветренной – 
| | | | Рис. 9.5. Схема потока около конуса,
наклоненного под углом атаки:
1 – ось конуса; 2 – ось скачка уплотнения; 3 – ось координат и направление 
| |
Из свойств конического потока следует, что значения его параметров не зависят от r, а являются функциями переменных  и и  . Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости . Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости  будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок одинаковы для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок одинаковы для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости  . Однако в связи с тем, что угол наклона скачка . Однако в связи с тем, что угол наклона скачка  неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла  . Из этого следует, что в целом несимметричный конический поток за скачком оказывается неизоэнтропическим. . Из этого следует, что в целом несимметричный конический поток за скачком оказывается неизоэнтропическим.
Теоретической основой для исследования такого потока являются уравнения движения идеальной среды и уравнение неразрывности в сферической системе координат. Решения системы дифференциальных уравнений находят в виде
 (9.9) (9.9)
Аналогичные выражения записывают и для остальных искомых параметров: составляющих скорости по соответствующим направлениям сферической системы координат  и и  , давления , давления  , плотности , плотности  , где , где  – это параметры симметричного обтекания на конусе с углом – это параметры симметричного обтекания на конусе с углом  . .
Каждое из уравнений (9.9) представляет собой ряд, в котором член, линейный по отношению к углу атаки, определяет решение в первом приближении, а квадратичный член – во втором. При малых углах  значения параметров будут мало отличаться от соответствующих значений при симметричном обтекании, и влияние угла значения параметров будут мало отличаться от соответствующих значений при симметричном обтекании, и влияние угла  достаточно учесть только линейными членами. С возрастанием достаточно учесть только линейными членами. С возрастанием  возникает необходимость вести расчет с учетом второго приближения, которым обычно и ограничиваются, полагая, что углы атаки невелики (что справедливо для баллистических ракет и ракет-носителей). возникает необходимость вести расчет с учетом второго приближения, которым обычно и ограничиваются, полагая, что углы атаки невелики (что справедливо для баллистических ракет и ракет-носителей).
Из выражений (9.9) следует, что определение параметров обтекания конуса под углом атаки начинается с решения частной задачи о симметричном потоке около того же конуса. В результате ее решения отыскиваются значения  в зависимости от угла в зависимости от угла  . Далее рассматривается влияние угла атаки. . Далее рассматривается влияние угла атаки.
Задача о влиянии угла атаки в первом приближении сводится к определению коэффициентов 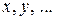 рядов (9.9) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (9.9) запишется следующим образом: рядов (9.9) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (9.9) запишется следующим образом:
 (9.10) (9.10)
В рассматриваемых уравнениях коэффициенты  можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты  и другие – во втором. Все эти коэффициенты зависят от одной переменной и другие – во втором. Все эти коэффициенты зависят от одной переменной  . .
Найденные в результате решения задачи коэффициенты x, y, z, отнесенные к максимальной скорости  , а также безразмерные величины , а также безразмерные величины  просчитаны для различных углов конуса и чисел просчитаны для различных углов конуса и чисел  и внесены в таблицы. При их помощи по формулам (9.10) ведется расчет скорости, давления и плотности численными методами (в аэродинамике наиболее развиты конечно-разностные методы) с помощью ЭВМ. Не вдаваясь в подробности расчетов, рассмотрим их результаты (рис. 9.6). и внесены в таблицы. При их помощи по формулам (9.10) ведется расчет скорости, давления и плотности численными методами (в аэродинамике наиболее развиты конечно-разностные методы) с помощью ЭВМ. Не вдаваясь в подробности расчетов, рассмотрим их результаты (рис. 9.6).

Рис. 9.6. Зависимости коэффициента давления:
а – от угла атаки; б – от угла ψ; в – от числа Маха
Простой логический анализ течения около конуса позволяет сделать вывод, что на его наветренной стороне ( ) давление должно быть больше, чем на подветренной. Это наглядно иллюстрируют приведенные качественные зависимости. С увеличением угла конуса давление возрастает на всей его поверхности. При малых углах атаки ) давление должно быть больше, чем на подветренной. Это наглядно иллюстрируют приведенные качественные зависимости. С увеличением угла конуса давление возрастает на всей его поверхности. При малых углах атаки  коэффициент давления коэффициент давления  практически линейно зависит от практически линейно зависит от  (рис. 9.6, а). С увеличением числа Маха набегающего потока (рис. 9.6, в) коэффициент давления монотонно уменьшается во всех меридиональных плоскостях. (рис. 9.6, а). С увеличением числа Маха набегающего потока (рис. 9.6, в) коэффициент давления монотонно уменьшается во всех меридиональных плоскостях.
Приближенный метод расчета.
Метод касательных конусов
Для приближенного расчета давления и коэффициента волнового сопротивления заостренных тел вращения произвольной формы применяется метод касательных (местных) конусов (рис. 9.7).
Согласно этому методу, коэффициент давления в каждой точке тела с криволинейной образующей принимается равным коэффициенту давления на местном конусе с углом полураствора  (при том же числе Маха). Образующей местного конуса является касательная к поверхности тела в данной точке, а осью конуса – ось потока, т. е. направление вектора скорости (при том же числе Маха). Образующей местного конуса является касательная к поверхности тела в данной точке, а осью конуса – ось потока, т. е. направление вектора скорости  (если угол атаки (если угол атаки  ) или продольная ось тела (при симметричном обтекании). То есть производят замену плавной образующей тела вращения на ломаную линию (исходное тело с криволинейной образующей заменяют составным коническим). Таким образом, можно приближенно определить закон распределения давления по телу вращения и рассчитать течение во всей области между скачком и телом. ) или продольная ось тела (при симметричном обтекании). То есть производят замену плавной образующей тела вращения на ломаную линию (исходное тело с криволинейной образующей заменяют составным коническим). Таким образом, можно приближенно определить закон распределения давления по телу вращения и рассчитать течение во всей области между скачком и телом.
 В случае аналитического задания формы тела определение угла местного конуса (угла наклона касательной) выполняется достаточно просто. Например, для носовой части, форма которой получена вращением дуги окружности радиуса В случае аналитического задания формы тела определение угла местного конуса (угла наклона касательной) выполняется достаточно просто. Например, для носовой части, форма которой получена вращением дуги окружности радиуса  вокруг некоторой оси, угол наклона касательной в точке с местным радиусом тела вращения вокруг некоторой оси, угол наклона касательной в точке с местным радиусом тела вращения  определяется по следующей формуле: определяется по следующей формуле:  , где , где  – радиус миделя (наибольшего поперечного сечения тела). – радиус миделя (наибольшего поперечного сечения тела).
 Аналогично, для оценки параметров на поверхности конуса при Аналогично, для оценки параметров на поверхности конуса при  можно воспользоваться результатами, полученными для можно воспользоваться результатами, полученными для  . Приближенные результаты можно получить, применив и для этого случая метод местных конусов (рис. 9.8). . Приближенные результаты можно получить, применив и для этого случая метод местных конусов (рис. 9.8).
В приложении к несимметричному обтеканию конуса делается предположение, что каждая образующая конуса, отклоненного на угол  , принадлежит условному конусу с углом , принадлежит условному конусу с углом  (местный угол), симметрично обтекаемому потоком ( (местный угол), симметрично обтекаемому потоком ( – подветренная образующая; – подветренная образующая; 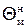 – наветренная). Имея результаты теории симметричного обтекания, можно определить параметры на той образующей, которая принадлежит этому «местному» конусу. Таким образом, основным элементом расчета является угол «местного конуса». – наветренная). Имея результаты теории симметричного обтекания, можно определить параметры на той образующей, которая принадлежит этому «местному» конусу. Таким образом, основным элементом расчета является угол «местного конуса».
Величину угла  можно рассчитать по формуле (9.8) или по приближенной формуле, применимой для малых углов можно рассчитать по формуле (9.8) или по приближенной формуле, применимой для малых углов  : :
 . (9.11) . (9.11)
В формуле (9.11)  отсчитывают от оси конуса, а угол отсчитывают от оси конуса, а угол  в формуле (9.8) – от вектора в формуле (9.8) – от вектора  (см. рис. 9.5). За начало отсчета обоих углов принято направление на подветренную образующую конуса, лежащую в плоскости симметрии течения (в плоскости «вектор скорости – ось конуса»). (см. рис. 9.5). За начало отсчета обоих углов принято направление на подветренную образующую конуса, лежащую в плоскости симметрии течения (в плоскости «вектор скорости – ось конуса»).
Чем больше скорость набегающего потока и меньше угол атаки, тем меньше погрешность расчетов по этому методу. Поэтому его целесообразно применять при малых углах  и больших числах и больших числах  . .
По распределению давления
Получим формулы для определения нормальной и продольной силы, а также момента тангажа относительно вершины для конуса, обтекаемого идеальной жидкостью. В этом случае на поверхность тела действуют только силы аэродинамического давления.
Выделим на поверхности тела элементарную площадку:  (рис. 9.9). Нормальная сила, действующая на эту площадку, равна (рис. 9.9). Нормальная сила, действующая на эту площадку, равна
 . .
 
Рис. 9.9. Определение нормальной и продольной силы
Так как 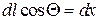 , после интегрирования в пределах , после интегрирования в пределах 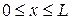  ( ( – длина тела вращения) и – длина тела вращения) и 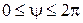 получим выражение для нормальной силы, действующей на всю поверхность тела: получим выражение для нормальной силы, действующей на всю поверхность тела:
 . .
Коэффициент нормальной силы равен 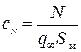 , где , где  – площадь миделевого сечения тела. Перейдем к безразмерным величинам и сделаем следующие замены: – площадь миделевого сечения тела. Перейдем к безразмерным величинам и сделаем следующие замены:  , ,  , , 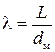 ( ( – удлинение тела; – удлинение тела;  – диаметр миделя). Тогда выражение для коэффициента нормальной силы примет вид – диаметр миделя). Тогда выражение для коэффициента нормальной силы примет вид
 , ,
 . (9.12) . (9.12)
Аналогично получим формулу для коэффициента продольной силы. Элементарная продольная сила равна  . Так как . Так как  , то , то
 и и  . (9.13) . (9.13)
Формулы (9.12) и (9.13) применимы для любого тела вращения. Для конуса 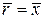 , , 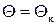 и и  . Тогда из формул (9.12) и (9.13) получим следующее: . Тогда из формул (9.12) и (9.13) получим следующее:
 , (9.14) , (9.14)
 . (9.15) . (9.15)
Коэффициент давления  . Коэффициент момента относительно вершины конуса, отнесенный к длине конуса . Коэффициент момента относительно вершины конуса, отнесенный к длине конуса  равен равен  . Из формул (9.14) и (9.15) следует, что коэффициенты . Из формул (9.14) и (9.15) следует, что коэффициенты  и и  зависят от углов атаки зависят от углов атаки  , полураствора конуса , полураствора конуса  и числа Маха и числа Маха  , т. е. , т. е.  . .
Анализ результатов экспериментов и расчетов для конусов показывает, что при увеличении  коэффициент нормальной силы уменьшается, а коэффициент продольной силы увеличивается. Подобное противоположное влияние на эти аэродинамические коэффициенты оказывает число Маха: с увеличением числа коэффициент нормальной силы уменьшается, а коэффициент продольной силы увеличивается. Подобное противоположное влияние на эти аэродинамические коэффициенты оказывает число Маха: с увеличением числа   увеличивается, а увеличивается, а  уменьшается. уменьшается.
Для тонких тел вращения
Рассмотрим обтекание тонкого удлиненного тела вращения при малом угле атаке. В этом случае возмущенный поток в окрестности тела мало отличается от невозмущенного. По методу малых возмущений потенциал скорости потока удовлетворяет линейному дифференциальному уравнению и может быть представлен в виде суммы трех составляющих (рис. 9.10):
 , ,
где  потенциал невозмущенного потока; потенциал невозмущенного потока;  – потенциал скорости возмущения при осесимметричном – потенциал скорости возмущения при осесимметричном  обтекании тела потоком со скоростью обтекании тела потоком со скоростью   – потенциал, возникающий при поперечном обтекании тела потоком со скоростью – потенциал, возникающий при поперечном обтекании тела потоком со скоростью  . .
Согласно линейной теории потенциал обтекания тонкого тела при сверхзвуковых скоростях описывается уравнением
 . .
а б в
Рис. 9.10. Тонкое тело вращения при малом угле атаки:
а – 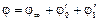 ; б – ; б –  в – в – 
В безразмерных координатах ( , ,  и и  , где , где  – диаметр миделевого сечения; – диаметр миделевого сечения;  – длина тела) уравнение для потенциала перепишется в виде – длина тела) уравнение для потенциала перепишется в виде
 . (9.16) . (9.16)
Для тонких тел 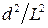 << 1, и, пренебрегая первым слагаемым в выражении (9.16) ввиду его малости, запишем следующее: << 1, и, пренебрегая первым слагаемым в выражении (9.16) ввиду его малости, запишем следующее:
 . (9.17) . (9.17)
Уравнение (9.17) есть ни что иное, как уравнение Лапласа – уравнение неразрывности для плоского потенциального течения несжимаемой жидкости. То есть поток в плоскости ZOY поперечного сечения тонкого тела можно считать двумерным, совпадающим с поперечным обтеканием цилиндра радиусом, равным местному радиусу тела вращения  , несжимаемой жидкостью. Кроме того, из уравнения (9.17) следует также, что потенциал обтекания тонкого тела не зависит от числа , несжимаемой жидкостью. Кроме того, из уравнения (9.17) следует также, что потенциал обтекания тонкого тела не зависит от числа  . .
В результате некоторых преобразований уравнения (9.17) и интегрирования по углу  получим выражение для нормальной силы, действующей на элемент тела вращения длиной получим выражение для нормальной силы, действующей на элемент тела вращения длиной  : :
 , (9.18) , (9.18)
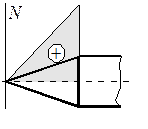
где  . Отсюда следует, что нормальная сила . Отсюда следует, что нормальная сила  появляется только на участках с переменной площадью поперечного сечения. Знак силы зависит от знака производной появляется только на участках с переменной площадью поперечного сечения. Знак силы зависит от знака производной  (рис. 9.11). (рис. 9.11).
а б
Рис. 9.11. Распределение нормальной силы по поверхности конуса:
а – цилиндрического тела; б – параболического тела
Носовая часть корпуса  создает положительную нормальную силу, а суживающаяся хвостовая часть создает положительную нормальную силу, а суживающаяся хвостовая часть  – отрицательную нормальную силу, тогда как цилиндрический отсек, для которого – отрицательную нормальную силу, тогда как цилиндрический отсек, для которого 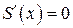 , при обтекании тела идеальной жидкостью не создает нормальной силы. , при обтекании тела идеальной жидкостью не создает нормальной силы.
Нормальная суммарная сила для тонкого тела вращения равна
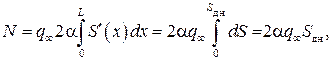
а коэффициент нормальной силы равен
 , (9.19) , (9.19)
где  – относительная площадь донного среза (угол – относительная площадь донного среза (угол  измеряется в радианах). Для носовой части измеряется в радианах). Для носовой части 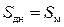 и и  независимо от формы носовой части и числа Маха. независимо от формы носовой части и числа Маха.
 Момент элементарной нормальной силы относительно вершины тела (рис. 9.12) – момент тангажа – равен Момент элементарной нормальной силы относительно вершины тела (рис. 9.12) – момент тангажа – равен  Знак «минус» в этой формуле говорит о том, что создаваемый момент – это момент на пикирование: Знак «минус» в этой формуле говорит о том, что создаваемый момент – это момент на пикирование:
 , ,
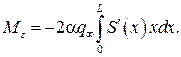
Коэффициент момента равен
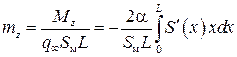 , ,
т. е. 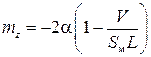 , где , где  – объем носовой части. – объем носовой части.
Рис. 9.14. Обтекание клина околозвуковым потоком
При увеличении скорости потока и приближении числа  к единице зона местных сверхзвуковых скоростей за угловой точкой расширяется в продольном и поперечном направлениях. Скачок уплотнения, замыкающий местную сверхзвуковую область, смещается вниз по потоку. В то же время в отрицательной «бесконечности» (в набегающем потоке) зарождается новый скачок уплотнения, который при увеличении числа к единице зона местных сверхзвуковых скоростей за угловой точкой расширяется в продольном и поперечном направлениях. Скачок уплотнения, замыкающий местную сверхзвуковую область, смещается вниз по потоку. В то же время в отрицательной «бесконечности» (в набегающем потоке) зарождается новый скачок уплотнения, который при увеличении числа  приближается к вершине клина и достигает ее. Таким образом, если при приближается к вершине клина и достигает ее. Таким образом, если при  местная сверхзвуковая зона располагается перед скачком уплотнения, то при местная сверхзвуковая зона располагается перед скачком уплотнения, то при  она располагается за ним. она располагается за ним.
Околозвуковое обтекание клина и конуса имеет общие особенности:
1. Звуковая скорость не может быть достигнута на каком-либо плоском участке поверхности. Во всем околозвуковом диапазоне скоростей звуковая скорость достигается вблизи угловой точки тела.
2. При числе  местное число Маха становится постоянным, т. е. местное число Маха становится постоянным, т. е. 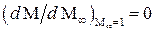 . Это значит, что местные числа Маха на поверхности клина или конуса при . Это значит, что местные числа Маха на поверхности клина или конуса при  остаются постоянными. Это явление называется законом стабилизации для трансзвуковых течений (например, для конуса с остаются постоянными. Это явление называется законом стабилизации для трансзвуковых течений (например, для конуса с  диапазон постоянства определяется значениями чисел Маха диапазон постоянства определяется значениями чисел Маха  ). ).
 Осесимметричный поток у конуса имеет некоторые отличия от потока около клина. Как уже говорилось, при сверхзвуковом обтекании конуса, в отличие от клина, параметры потока одинаковы только на конических поверхностях (а не во всей области между скачком и поверхностью). При обтекании конуса поток в области между скачком и конусом претерпевает дополнительное изоэнтропическое сжатие. То есть при некоторых малых сверхзвуковых числах Маха поток за скачком еще сверхзвуковой, а ближе к поверхности конуса может стать дозвуковым (рис. 9.15). Таким образом, наблюдается плавный переход от сверхзвуковых скоростей к дозвуковым. За скачком уплотнения может существовать дозвуковая зона, вклинивающаяся в область сверхзвукового течения и примыкающая к поверхности конуса. При еще меньших сверхзвуковых скоростях поток уже не является коническим. Осесимметричный поток у конуса имеет некоторые отличия от потока около клина. Как уже говорилось, при сверхзвуковом обтекании конуса, в отличие от клина, параметры потока одинаковы только на конических поверхностях (а не во всей области между скачком и поверхностью). При обтекании конуса поток в области между скачком и конусом претерпевает дополнительное изоэнтропическое сжатие. То есть при некоторых малых сверхзвуковых числах Маха поток за скачком еще сверхзвуковой, а ближе к поверхности конуса может стать дозвуковым (рис. 9.15). Таким образом, наблюдается плавный переход от сверхзвуковых скоростей к дозвуковым. За скачком уплотнения может существовать дозвуковая зона, вклинивающаяся в область сверхзвукового течения и примыкающая к поверхности конуса. При еще меньших сверхзвуковых скоростях поток уже не является коническим.
В околозвуковом диапазоне скоростей появляется дополнительное волновое сопротивление, которое приводит к резкому возрастанию полного сопротивления тела (так называемый волновой кризис). Следует отметить, что заметное возрастание коэффициента сопротивления за счет волнового сопротивления проявляется при числах Маха  . .
 Экспериментальные данные для тел вращения показывают следующее: Экспериментальные данные для тел вращения показывают следующее:
1. Коэффициент лобового сопротивления достигает своего максимума при числах Маха, несколько больших числа  , в интервале , в интервале  . .
2. Доминирующее влияние на величину  оказывает форма головной части (рис. 9.16). оказывает форма головной части (рис. 9.16).
При числах  для определения характеристик ЛА в основном используют результаты эксперимента. При числах Маха, близких к единице (область действия закона трансзвуковой стабилизации), расчет характеристик ведут по данным для для определения характеристик ЛА в основном используют результаты эксперимента. При числах Маха, близких к единице (область действия закона трансзвуковой стабилизации), расчет характеристик ведут по данным для  с учетом их градиента. Например, по известным данным для с учетом их градиента. Например, по известным данным для  при при  можно рассчитать коэффициент сопротивления для чисел Маха можно рассчитать коэффициент сопротивления для чисел Маха  . Или наоборот, можно экстраполировать данные для чисел Маха, близких к единице, на число Маха . Или наоборот, можно экстраполировать данные для чисел Маха, близких к единице, на число Маха  . .
Приближенная теория Ньютона
При гиперзвуковых скоростях полета распределение давления по поверхности тела в области до миделевого сечения позволяет определить приближенная теория Ньютона. Согласно теории Ньютона, в которой принята идеализированная модель среды:
а) газообразная среда состоит из не взаимодействующих между собой частиц;
б) скорость движения частиц среды вплоть до столкновения их с поверхностью равна скорости набегающего невозмущенного потока  ; ;
в) при столкновении частиц с поверхностью нормальная составляющая скорости  (рис. 9.17) становится равной нулю, а касательная составляющая остается неизменной, т. е. давление в данной точке тела зависит только от ориентации соответствующего элемента поверхности относительно вектора (рис. 9.17) становится равной нулю, а касательная составляющая остается неизменной, т. е. давление в данной точке тела зависит только от ориентации соответствующего элемента поверхности относительно вектора  , а форма остальной части тела не влияет на давление в данной точке. , а форма остальной части тела не влияет на давление в данной точке.
 При больших скоростях движения, когда числа При больших скоростях движения, когда числа  , скачок уплотнения практически ложится на поверхность тела, в случае разреженной среды (гиперзвуковые скорости полета характерны для разреженной верхней части атмосферы) характер обтекания тел близок к приближенной схеме Ньютона. , скачок уплотнения практически ложится на поверхность тела, в случае разреженной среды (гиперзвуковые скорости полета характерны для разреженной верхней части атмосферы) характер обтекания тел близок к приближенной схеме Ньютона.
 Теория Ньютона позволяет рассчитать давление на всей поверхности, «освещаемой» набегающим потоком, т. е. в области, где частицы набегающего потока имеют возможность взаимодействовать с поверхностью. Согласно этой теории на участках в аэродинамической тени давление во всех точках равно Теория Ньютона позволяет рассчитать давление на всей поверхности, «освещаемой» набегающим потоком, т. е. в области, где частицы набегающего потока имеют возможность взаимодействовать с поверхностью. Согласно этой теории на участках в аэродинамической тени давление во всех точках равно  и коэффициент давления и коэффициент давления  (рис. 9.18). (рис. 9.18).
Рассмотрим порядок определения давления на поверхности тела вне области аэродинамической тени. Выделим элемент поверхности  с местным углом атаки с местным углом атаки  (см. рис. 9.17). Масса газа, сталкивающегося с этой площадкой в единицу времени, равна (см. рис. 9.17). Масса газа, сталкивающегося с этой площадкой в единицу времени, равна  , а количество движения этой массы – , а количество движения этой массы –  . .
После соударения с поверхностью нормальная составляющая скорости  . Изменение количества движения рассматриваемой массы газа приравняем к импульсу силы давления: . Изменение количества движения рассматриваемой массы газа приравняем к импульсу силы давления:
 . .
Вспоминая выражение для коэффициента давления  , после простых преобразований можем записать , после простых преобразований можем записать
 . (9.20) . (9.20)
Формула (9.20) является следствием теории Ньютона. Согласно ей коэффициент давления в данной точке поверхности тела зависит только от местного угла атаки поверхности, т. е.  . В точке полного торможения потока ( . В точке полного торможения потока ( ) коэффициент давления имеет постоянное, не зависящее от числа Маха набегающего потока значение, равное ) коэффициент давления имеет постоянное, не зависящее от числа Маха набегающего потока значение, равное 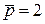 , что не соответствует действительности. , что не соответствует действительности.
Чтобы при расчете можно было учесть влияние формы тела и числа Маха  на распределение давления по поверхности тела произвольной формы, в исходную формулу Ньютона (9.20) вводится уточнение. Один из вариантов уточнения приводит к следующему виду формулы Ньютона: на распределение давления по поверхности тела произвольной формы, в исходную формулу Ньютона (9.20) вводится уточнение. Один из вариантов уточнения приводит к следующему виду формулы Ньютона:
 . (9.21) . (9.21)
В таком варианте уточнения считается, что значение коэффициента давления  в некоторой фиксированной точке тела, рассчитанное по приближенной формуле (9.21), должно совпадать с точным значением в некоторой фиксированной точке тела, рассчитанное по приближенной формуле (9.21), должно совпадать с точным значением  в этой точке, имеющей местный угол атаки поверхности в этой точке, имеющей местный угол атаки поверхности  . .
В качестве фиксированных точек для разных геометрических форм выбирают характерные для данной конфигурации точки (рис. 9.19), в которых значение давления можно рассчитать или приближенно оценить другими методами:
– в случае заостренного тела – точка у острия тела; в данном случае  = =  , т. е. углу при вершине обтекаемого тела (или углу конусности наконечника), а величина , т. е. углу при вершине обтекаемого тела (или углу конусности наконечника), а величина  равна равна  для какой-либо образующей этого наконечника; для какой-либо образующей этого наконечника;
– для затупленных тел – передняя критическая точка, располагающаяся за прямым скачком уплотнения, для которой  , а давление равно давлению торможения за прямым скачком , а давление равно давлению торможения за прямым скачком  , и расчетная формула примет вид , и расчетная формула примет вид 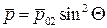 . .

Рис. 9.19. Схема к выбору фиксированной точки
В заключение следует еще раз отметить, что теория Ньютона может быть использована только при исследовании обтекания тел потоком сильно разреженного газа при очень больших скоростях движения, т. е. тогда, когда допущения, лежащие в основе этой теории, становятся справедливыми.
Таким образом, в главе были рассмотрены вопросы расчета симметричного и несимметричного обтекания корпусов ЛА, особенности, характеризующие диапазоны околозвуковых и гиперзвуковых скоростей.
Контрольные вопросы и задания
1. Чему равны скорости течения в некоторых точках потока, если коэффициент давления  в первой точке равен единице, а во второй – нулю? Какая из этих точек является критической? в первой точке равен единице, а во второй – нулю? Какая из этих точек является критической?
2. Для каких целей используются результаты решения задачи о симметричном обтекании конуса сверхзвуковым потоком?
3. В чем заключаются отличия в обтекании конуса и клина сверхзвуковым потоком газа? Почему за коническим скачком уплотнения линия тока становится криволинейной?
4. Дайте определение осесимметричного и конического потока. Можно ли течение считать коническим для конуса, обтекаемого под углом атаки 
5. В чем суть метода «местных» конусов? Постройте «местные» конусы для наветренной и подветренной образующей конуса для некоторого угла атаки  . Какие ограничения накладываются на величину угла атаки? . Какие ограничения накладываются на величину угла атаки?
6. Рассчитайте величины коэффициентов нормальной и продольной силы для симметрично обтекаемого конуса с углом полураствора 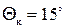 , если известно, что значение коэффициента давления на поверхности конуса равно , если известно, что значение коэффициента давления на поверхности конуса равно  . Воспользуйтесь следующими формулами: . Воспользуйтесь следующими формулами:  и и  . .
7. Какой диапазон скоростей называют околозвуковым? В чем заключаются основные особенности околозвуковых скоростей? Сформулируйте суть закона трансзвуковой стабилизации.
8. В чем заключаются основные особенности гиперзвуковых течений? Опишите модель среды, принятую И. Ньютоном для своей теории расчета силы сопротивления, возникающей при движении тел в воздушной среде. Для какой среды и при каких скоростях движения тела в реальной ситуации справедлива теория Ньютона?
Глава 9
ОБТЕКАНИЕ ТЕЛ ВРАЩЕНИЯ
СВЕРХЗВУКОВЫМ ПОТОКОМ
Коническим называют поток, в котором параметры газа на конической поверхности сохраняются постоянными. Они изменяются только при переходе с одной конической поверхности на другую.
Осесимметричным называют течение, обладающее симметрией относительно оси тела. В этом случае течение газа во всех меридиональных плоскостях одинаково, и движение газа можно изучать как плоское в одной из меридиональных плоскостей.
Осесимметричное обтекание острого конуса
Рассмотрим осесимметричное ( ) обтекание конуса с углом полураствора ) обтекание конуса с углом полураствора  сверхзвуковым потоком. сверхзвуковым потоком.
Результаты решения задачи осесимметричного обтекания острого конуса используются в следующих случаях:
а) для определения коэффициента волнового сопротивления конических головных частей корпусов ЛА;
б) в качестве исходных данных для численного расчета обтекания конусов при  ; ;
в) в качестве начальной точки при расчете обтекания тел с криволинейной образующей;
г) для приближенного расчета распределения давления по поверхности тел более сложной формы.
 При симметричном обтекании конуса с углом полураствора При симметричном обтекании конуса с углом полураствора  ( ( при заданном числе Маха при заданном числе Маха  ) перед ним возникает присоединенный конический скачок уплотнения с вершиной в вершине конуса (рис. 9.1). Задача расчета обтекания конуса сводится к нахождению угла полураствора конического скачка ) перед ним возникает присоединенный конический скачок уплотнения с вершиной в вершине конуса (рис. 9.1). Задача расчета обтекания конуса сводится к нахождению угла полураствора конического скачка  и поля скоростей (и давлений) между скачком уплотнения и конусом. Поскольку поток около конуса осессимметричный, то будем рассматривать одну меридиональную плоскость. Довольно просто убедиться, что для всех плоскостей, перпендикулярных продольной оси конуса, граничные условия (при и поля скоростей (и давлений) между скачком уплотнения и конусом. Поскольку поток около конуса осессимметричный, то будем рассматривать одну меридиональную плоскость. Довольно просто убедиться, что для всех плоскостей, перпендикулярных продольной оси конуса, граничные условия (при 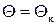 и и  ) одинаковы, и течения между конусом и скачком уплотнения геометрически подобны. То есть в сходственных точках этих сечений параметры потока ( ) одинаковы, и течения между конусом и скачком уплотнения геометрически подобны. То есть в сходственных точках этих сечений параметры потока ( , ,  ) одинаковы. Геометрическим местом сходственных точек являются конические поверхности, расположенные между поверхностью конуса и скачком уплотнения. Течения подобного рода называются коническими. ) одинаковы. Геометрическим местом сходственных точек являются конические поверхности, расположенные между поверхностью конуса и скачком уплотнения. Течения подобного рода называются коническими.
Задача решается в полярной системе координат  с полюсом в вершине конуса. Зафиксируем некоторую промежуточную коническую поверхность с углом полураствора с полюсом в вершине конуса. Зафиксируем некоторую промежуточную коническую поверхность с углом полураствора  . Вследствие конического характера течения составляющие скорости потока на этой поверхности не зависят от координаты . Вследствие конического характера течения составляющие скорости потока на этой поверхности не зависят от координаты  | 


 поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры газа в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат
поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры газа в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат  (рис. 9.5), выбранной таким образом, что координате
(рис. 9.5), выбранной таким образом, что координате  соответствует вершина конуса, оси координат
соответствует вершина конуса, оси координат  (ось 3) – направление скорости набегающего потока, а меридиональной плоскости
(ось 3) – направление скорости набегающего потока, а меридиональной плоскости 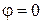 – плоскость, проходящая через ось 3 и ось 1, т. е. ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом
– плоскость, проходящая через ось 3 и ось 1, т. е. ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом  (на рис. 9.5 этот угол отрицательный), будет следующим:
(на рис. 9.5 этот угол отрицательный), будет следующим: , (9.8)
, (9.8) – сферическая координата для образующей конуса. Для подветренной образующей
– сферическая координата для образующей конуса. Для подветренной образующей 


 . Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости
. Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости  будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок одинаковы для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости
будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок одинаковы для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости  неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла
неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла  (9.9)
(9.9) и
и  , давления
, давления  , плотности
, плотности  , где
, где  – это параметры симметричного обтекания на конусе с углом
– это параметры симметричного обтекания на конусе с углом  в зависимости от угла
в зависимости от угла 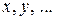 рядов (9.9) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (9.9) запишется следующим образом:
рядов (9.9) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (9.9) запишется следующим образом: (9.10)
(9.10) можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты
можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты  и другие – во втором. Все эти коэффициенты зависят от одной переменной
и другие – во втором. Все эти коэффициенты зависят от одной переменной  , а также безразмерные величины
, а также безразмерные величины  просчитаны для различных углов конуса и чисел
просчитаны для различных углов конуса и чисел  и внесены в таблицы. При их помощи по формулам (9.10) ведется расчет скорости, давления и плотности численными методами (в аэродинамике наиболее развиты конечно-разностные методы) с помощью ЭВМ. Не вдаваясь в подробности расчетов, рассмотрим их результаты (рис. 9.6).
и внесены в таблицы. При их помощи по формулам (9.10) ведется расчет скорости, давления и плотности численными методами (в аэродинамике наиболее развиты конечно-разностные методы) с помощью ЭВМ. Не вдаваясь в подробности расчетов, рассмотрим их результаты (рис. 9.6).
 ) давление должно быть больше, чем на подветренной. Это наглядно иллюстрируют приведенные качественные зависимости. С увеличением угла конуса давление возрастает на всей его поверхности. При малых углах атаки
) давление должно быть больше, чем на подветренной. Это наглядно иллюстрируют приведенные качественные зависимости. С увеличением угла конуса давление возрастает на всей его поверхности. При малых углах атаки  коэффициент давления
коэффициент давления  практически линейно зависит от
практически линейно зависит от  (при том же числе Маха). Образующей местного конуса является касательная к поверхности тела в данной точке, а осью конуса – ось потока, т. е. направление вектора скорости
(при том же числе Маха). Образующей местного конуса является касательная к поверхности тела в данной точке, а осью конуса – ось потока, т. е. направление вектора скорости  (если угол атаки
(если угол атаки  В случае аналитического задания формы тела определение угла местного конуса (угла наклона касательной) выполняется достаточно просто. Например, для носовой части, форма которой получена вращением дуги окружности радиуса
В случае аналитического задания формы тела определение угла местного конуса (угла наклона касательной) выполняется достаточно просто. Например, для носовой части, форма которой получена вращением дуги окружности радиуса  вокруг некоторой оси, угол наклона касательной в точке с местным радиусом тела вращения
вокруг некоторой оси, угол наклона касательной в точке с местным радиусом тела вращения  определяется по следующей формуле:
определяется по следующей формуле:  , где
, где  – радиус миделя (наибольшего поперечного сечения тела).
– радиус миделя (наибольшего поперечного сечения тела). Аналогично, для оценки параметров на поверхности конуса при
Аналогично, для оценки параметров на поверхности конуса при  . Приближенные результаты можно получить, применив и для этого случая метод местных конусов (рис. 9.8).
. Приближенные результаты можно получить, применив и для этого случая метод местных конусов (рис. 9.8). (местный угол), симметрично обтекаемому потоком (
(местный угол), симметрично обтекаемому потоком ( – подветренная образующая;
– подветренная образующая; 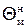 – наветренная). Имея результаты теории симметричного обтекания, можно определить параметры на той образующей, которая принадлежит этому «местному» конусу. Таким образом, основным элементом расчета является угол «местного конуса».
– наветренная). Имея результаты теории симметричного обтекания, можно определить параметры на той образующей, которая принадлежит этому «местному» конусу. Таким образом, основным элементом расчета является угол «местного конуса». . (9.11)
. (9.11) отсчитывают от оси конуса, а угол
отсчитывают от оси конуса, а угол  (рис. 9.9). Нормальная сила, действующая на эту площадку, равна
(рис. 9.9). Нормальная сила, действующая на эту площадку, равна .
.

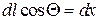 , после интегрирования в пределах
, после интегрирования в пределах 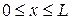
 (
( – длина тела вращения) и
– длина тела вращения) и 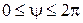 получим выражение для нормальной силы, действующей на всю поверхность тела:
получим выражение для нормальной силы, действующей на всю поверхность тела: .
.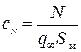 , где
, где  – площадь миделевого сечения тела. Перейдем к безразмерным величинам и сделаем следующие замены:
– площадь миделевого сечения тела. Перейдем к безразмерным величинам и сделаем следующие замены:  ,
,  ,
, 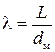 (
( – удлинение тела;
– удлинение тела;  – диаметр миделя). Тогда выражение для коэффициента нормальной силы примет вид
– диаметр миделя). Тогда выражение для коэффициента нормальной силы примет вид ,
, . (9.12)
. (9.12) . Так как
. Так как  , то
, то и
и  . (9.13)
. (9.13)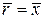 ,
, 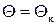 и
и  . Тогда из формул (9.12) и (9.13) получим следующее:
. Тогда из формул (9.12) и (9.13) получим следующее: , (9.14)
, (9.14) . (9.15)
. (9.15) . Коэффициент момента относительно вершины конуса, отнесенный к длине конуса
. Коэффициент момента относительно вершины конуса, отнесенный к длине конуса  равен
равен  . Из формул (9.14) и (9.15) следует, что коэффициенты
. Из формул (9.14) и (9.15) следует, что коэффициенты  и
и  зависят от углов атаки
зависят от углов атаки  .
. увеличивается, а
увеличивается, а  ,
, потенциал невозмущенного потока;
потенциал невозмущенного потока;  – потенциал скорости возмущения при осесимметричном
– потенциал скорости возмущения при осесимметричном  обтекании тела потоком со скоростью
обтекании тела потоком со скоростью 
 – потенциал, возникающий при поперечном обтекании тела потоком со скоростью
– потенциал, возникающий при поперечном обтекании тела потоком со скоростью  .
. .
.
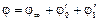 ; б –
; б –  в –
в – 
 и
и  , где
, где  – диаметр миделевого сечения;
– диаметр миделевого сечения;  . (9.16)
. (9.16)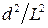 << 1, и, пренебрегая первым слагаемым в выражении (9.16) ввиду его малости, запишем следующее:
<< 1, и, пренебрегая первым слагаемым в выражении (9.16) ввиду его малости, запишем следующее: . (9.17)
. (9.17) , несжимаемой жидкостью. Кроме того, из уравнения (9.17) следует также, что потенциал обтекания тонкого тела не зависит от числа
, несжимаемой жидкостью. Кроме того, из уравнения (9.17) следует также, что потенциал обтекания тонкого тела не зависит от числа  получим выражение для нормальной силы, действующей на элемент тела вращения длиной
получим выражение для нормальной силы, действующей на элемент тела вращения длиной  :
: , (9.18)
, (9.18) . Отсюда следует, что нормальная сила
. Отсюда следует, что нормальная сила  появляется только на участках с переменной площадью поперечного сечения. Знак силы зависит от знака производной
появляется только на участках с переменной площадью поперечного сечения. Знак силы зависит от знака производной  (рис. 9.11).
(рис. 9.11).

 создает положительную нормальную силу, а суживающаяся хвостовая часть
создает положительную нормальную силу, а суживающаяся хвостовая часть  – отрицательную нормальную силу, тогда как цилиндрический отсек, для которого
– отрицательную нормальную силу, тогда как цилиндрический отсек, для которого 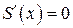 , при обтекании тела идеальной жидкостью не создает нормальной силы.
, при обтекании тела идеальной жидкостью не создает нормальной силы.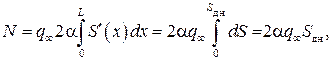
 , (9.19)
, (9.19) – относительная площадь донного среза (угол
– относительная площадь донного среза (угол 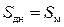 и
и  независимо от формы носовой части и числа Маха.
независимо от формы носовой части и числа Маха. Момент элементарной нормальной силы относительно вершины тела (рис. 9.12) – момент тангажа – равен
Момент элементарной нормальной силы относительно вершины тела (рис. 9.12) – момент тангажа – равен  Знак «минус» в этой формуле говорит о том, что создаваемый момент – это момент на пикирование:
Знак «минус» в этой формуле говорит о том, что создаваемый момент – это момент на пикирование: ,
,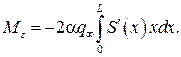
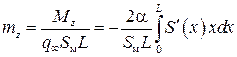 ,
,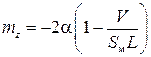 , где
, где  – объем носовой части.
– объем носовой части. местная сверхзвуковая зона располагается перед скачком уплотнения, то при
местная сверхзвуковая зона располагается перед скачком уплотнения, то при  она располагается за ним.
она располагается за ним. местное число Маха становится постоянным, т. е.
местное число Маха становится постоянным, т. е. 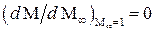 . Это значит, что местные числа Маха на поверхности клина или конуса при
. Это значит, что местные числа Маха на поверхности клина или конуса при  остаются постоянными. Это явление называется законом стабилизации для трансзвуковых течений (например, для конуса с
остаются постоянными. Это явление называется законом стабилизации для трансзвуковых течений (например, для конуса с  диапазон постоянства определяется значениями чисел Маха
диапазон постоянства определяется значениями чисел Маха  ).
). Осесимметричный поток у конуса имеет некоторые отличия от потока около клина. Как уже говорилось, при сверхзвуковом обтекании конуса, в отличие от клина, параметры потока одинаковы только на конических поверхностях (а не во всей области между скачком и поверхностью). При обтекании конуса поток в области между скачком и конусом претерпевает дополнительное изоэнтропическое сжатие. То есть при некоторых малых сверхзвуковых числах Маха поток за скачком еще сверхзвуковой, а ближе к поверхности конуса может стать дозвуковым (рис. 9.15). Таким образом, наблюдается плавный переход от сверхзвуковых скоростей к дозвуковым. За скачком уплотнения может существовать дозвуковая зона, вклинивающаяся в область сверхзвукового течения и примыкающая к поверхности конуса. При еще меньших сверхзвуковых скоростях поток уже не является коническим.
Осесимметричный поток у конуса имеет некоторые отличия от потока около клина. Как уже говорилось, при сверхзвуковом обтекании конуса, в отличие от клина, параметры потока одинаковы только на конических поверхностях (а не во всей области между скачком и поверхностью). При обтекании конуса поток в области между скачком и конусом претерпевает дополнительное изоэнтропическое сжатие. То есть при некоторых малых сверхзвуковых числах Маха поток за скачком еще сверхзвуковой, а ближе к поверхности конуса может стать дозвуковым (рис. 9.15). Таким образом, наблюдается плавный переход от сверхзвуковых скоростей к дозвуковым. За скачком уплотнения может существовать дозвуковая зона, вклинивающаяся в область сверхзвукового течения и примыкающая к поверхности конуса. При еще меньших сверхзвуковых скоростях поток уже не является коническим. .
. Экспериментальные данные для тел вращения показывают следующее:
Экспериментальные данные для тел вращения показывают следующее: .
. оказывает форма головной части (рис. 9.16).
оказывает форма головной части (рис. 9.16). (рис. 9.17) становится равной нулю, а касательная составляющая остается неизменной, т. е. давление в данной точке тела зависит только от ориентации соответствующего элемента поверхности относительно вектора
(рис. 9.17) становится равной нулю, а касательная составляющая остается неизменной, т. е. давление в данной точке тела зависит только от ориентации соответствующего элемента поверхности относительно вектора  , а форма остальной части тела не влияет на давление в данной точке.
, а форма остальной части тела не влияет на давление в данной точке. При больших скоростях движения, когда числа
При больших скоростях движения, когда числа  , скачок уплотнения практически ложится на поверхность тела, в случае разреженной среды (гиперзвуковые скорости полета характерны для разреженной верхней части атмосферы) характер обтекания тел близок к приближенной схеме Ньютона.
, скачок уплотнения практически ложится на поверхность тела, в случае разреженной среды (гиперзвуковые скорости полета характерны для разреженной верхней части атмосферы) характер обтекания тел близок к приближенной схеме Ньютона. Теория Ньютона позволяет рассчитать давление на всей поверхности, «освещаемой» набегающим потоком, т. е. в области, где частицы набегающего потока имеют возможность взаимодействовать с поверхностью. Согласно этой теории на участках в аэродинамической тени давление во всех точках равно
Теория Ньютона позволяет рассчитать давление на всей поверхности, «освещаемой» набегающим потоком, т. е. в области, где частицы набегающего потока имеют возможность взаимодействовать с поверхностью. Согласно этой теории на участках в аэродинамической тени давление во всех точках равно  и коэффициент давления
и коэффициент давления  (рис. 9.18).
(рис. 9.18). с местным углом атаки
с местным углом атаки  , а количество движения этой массы –
, а количество движения этой массы –  .
. . Изменение количества движения рассматриваемой массы газа приравняем к импульсу силы давления:
. Изменение количества движения рассматриваемой массы газа приравняем к импульсу силы давления: .
. , после простых преобразований можем записать
, после простых преобразований можем записать . (9.20)
. (9.20) . В точке полного торможения потока (
. В точке полного торможения потока ( ) коэффициент давления имеет постоянное, не зависящее от числа Маха набегающего потока значение, равное
) коэффициент давления имеет постоянное, не зависящее от числа Маха набегающего потока значение, равное 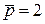 , что не соответствует действительности.
, что не соответствует действительности. . (9.21)
. (9.21) в некоторой фиксированной точке тела, рассчитанное по приближенной формуле (9.21), должно совпадать с точным значением
в некоторой фиксированной точке тела, рассчитанное по приближенной формуле (9.21), должно совпадать с точным значением  в этой точке, имеющей местный угол атаки поверхности
в этой точке, имеющей местный угол атаки поверхности  .
. , а давление равно давлению торможения за прямым скачком
, а давление равно давлению торможения за прямым скачком  , и расчетная формула примет вид
, и расчетная формула примет вид 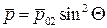 .
.

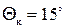 , если известно, что значение коэффициента давления на поверхности конуса равно
, если известно, что значение коэффициента давления на поверхности конуса равно  . Воспользуйтесь следующими формулами:
. Воспользуйтесь следующими формулами:  и
и  .
.
 ) обтекание конуса с углом полураствора
) обтекание конуса с углом полураствора  При симметричном обтекании конуса с углом полураствора
При симметричном обтекании конуса с углом полураствора  при заданном числе Маха
при заданном числе Маха  ) одинаковы, и течения между конусом и скачком уплотнения геометрически подобны. То есть в сходственных точках этих сечений параметры потока (
) одинаковы, и течения между конусом и скачком уплотнения геометрически подобны. То есть в сходственных точках этих сечений параметры потока ( ,
,  ) одинаковы. Геометрическим местом сходственных точек являются конические поверхности, расположенные между поверхностью конуса и скачком уплотнения. Течения подобного рода называются коническими.
) одинаковы. Геометрическим местом сходственных точек являются конические поверхности, расположенные между поверхностью конуса и скачком уплотнения. Течения подобного рода называются коническими. с полюсом в вершине конуса. Зафиксируем некоторую промежуточную коническую поверхность с углом полураствора
с полюсом в вершине конуса. Зафиксируем некоторую промежуточную коническую поверхность с углом полураствора 


