Решение задач линейного программирования в Excel

В повседневной жизни мы часто сталкиваемся с необходимостью решать оптимизационные задачи. Менеджеры, экономисты постоянно сталкиваются с разнообразными проблемами, начиная с планирования штата сотрудников, фонда зарплаты и составлением оптимального плана производства, планированием рекламной компании по продвижению продукции на рынок и оптимизацией капиталовложений.

В настоящее время наиболее мощным средством решения таких задач на компьютере является пакет Excel с его надстройкой «Поиск решения».

Это средство позволяет получить не только значения неизвестных, целевой функции и правых частей ограничений, но и ряд важных, дополнительных сведений:

- пределов изменения целевых коэффициентов и правых частей ограничений, в границах которых решение поставленной задачи возможно;

- нормированные стоимости единицы определяемых неизвестных;

- теневые цены единиц объемов предложенных ресурсов.

Благодаря этим сведениям, становится возможным вносить экономически обоснованные рекомендации в рассматриваемую данной задачей ситуацию, что очень необходимо любому экономисту.

Для решения задачи в Excel необходимо правильно поместить математическую модель по ячейкам электронной таблицы при этом целесообразно придерживаться таблицы2 заполнения ячеек.

 

Таблица2

 

Название задачи	Количество ячеек равное количеству переменных
Искомые перемен.	Список имен или обозначений ← переменных →
Значения перемен.	Соответствующие значения неизвестных (в начале не указываются)
Коэффиц. при переменн.	Перечень коэффициентов целевой функции	=Формула цели
Список ограничений	Нормативные коэффициенты при переменных в рассматриваемых ограничениях	=Формулы левых частей ограничений	Объемы ограничений

 

В ячейках, содержащих формулы (они выделены) чаще всего используется функция СУММПРОИЗВ (массив1;массив2), где массив1 – это перечень ячеек для значений переменных, в таблице они обведены пунктиром, а массив2 – коэффициенты при переменных. Обычно ячейки массива1 фиксируются, т.е. их адреса делают абсолютными, для того чтобы иметь возможность писать формулу только один раз, а во всех остальных случаях ее копировать.

Все сведения о модели заносят в окно «Поиск решения» (рис.8).

Для занесения адресов целевой функции и изменяемых переменных достаточно щелкнуть мышью по соответствующим ячейкам. Для занесения ограничений надо сообщать адрес ячейки, где находится соответствующая ограничению формула, сообщить вид неравенства и значение или адрес, где хранится значение правой части ограничения. Все эти действия выполняют по кнопке «Добавить» окна «Поиск решения». По этой кнопке появляется дополнительное окно для ввода ограничения. Несложно догадаться о назначении всех иных кнопок окна «Поиск решения».

По кнопке «Параметры» этого окна необходимо перейти в дополнительное окно, где обязательно следует отметить условие, что данная модель является линейной, а также можно принять условие не отрицательности переменных.

 

Рис. 8

Продемонстрируем использование «Поиска решения» на примере.

Условие задачи. Найти минимум функции Z = X₁ + X₂ при выполнении следующей системы ограничений:

3x₁ + x₂ ≥ 8

x₁- 4x₂ ≤ 19

2x₁ + 3x₂ ≤ 28

x₁- x₂ ≤ 4

x₁+ 3x₂ ≥ 8

В электронном процессоре Excel условие задачи можно представить так, как на рис. 9:

Задача
переменные	X1	X2
значения			Z
коэф.-ты
	Ограничения		Формулы	Знак	Объем
1-ое				>=
2-ое		-4		<=
3-е				<=
4-ое		-1		<=
5-ое				>=

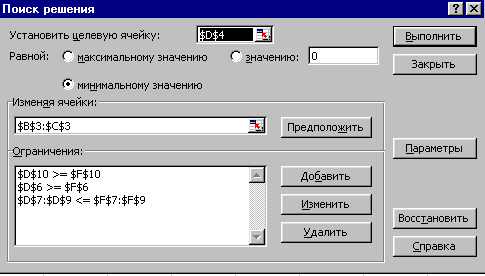
Рис. 9

Тогда окно Поиска решения будет выглядеть так рис.10:

Рис.10

Следует заметить, что при записи ограничений указывается сравнение адреса ячейки, хранящей формулу соответствующего ограничения с адресом, где хранится значение объема данного ограничения. Это связано с тем, что окно записи ограничения не позволяет записывать саму формулу ограничения, а предполагает лишь запись адресов. Полезно напомнить также, что запись адресов в окне «Поиск решения» целесообразнее делать не с клавиатуры, а с помощью мыши так называемым методом «взять и тащить».

По этому окну будет получен следующий результат см. (рис. 11):

 

Рис. 11

В ячейке D4 имеем минимальное значение целевой функции равное 4. Оптимальные значения переменных в ячейках B3 и C3 равны по 2.

Все ограничения выполняются. В частности, 2-ое ограничение: по его формуле результат равен 6, а его объем равен 19, следовательно, левая часть меньше правой на 25.