
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная оптимизационная задачаСодержание книги
Поиск на нашем сайте
Рассмотрим задачу планирования производства. Фабрика выпускает два типа строительных материалов А и В. Продукция обоих видов поступает в продажу. Для производства материалов используется два исходных продукта: I и II. Максимально возможные суточные запасы этих продуктов составляют 7 и 9 тонн соответственно. Расходы продуктов I и II на 1 тонну соответствующих материалов приведены в таблице3 Расход продуктов Таблица3
Изучение рынка сбыта показало, что суточный спрос на материал В не превышает спроса на материал А более чем на 1т. Кроме того, спрос на материал А не превышает 3т. в сутки. Оптовые цены одной тонны материалов равны: 4000 у.е. для материала В и 3000 у.е. для материала А. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным? Для решения этой задачи необходимо построить математическую модель. РЕШЕНИЕ 1. Формулировка математической модели задачи: · Переменные для решения задачи: · X2 – суточный обьем производства материала B; · определение функции цели (критерий оптимизации).Суммарная суточная прибыль от производства X1 материала А и X2 материала В равна: F = 4000X2 + 3000X1 · поэтому цель фабрики – среди всех допустимых значений X2 и X1 найти такие, которые максимизируют суммарную прибыль от производства материалов F: F = 4000X2 + 3000X1 Ограничения на переменные: § Обьем производства материалов не может быть отрицательным, т. е.: X2 ≥ 0, X1 ≥ 0; § Расход исходного продукты для производства обоих видов материалов не может превосходить максимально возможного запаса данного исходного продукта, т.е.: 2X2 + 3X1 ≤ 7; 3X2 + 2X1 ≤ 9. § Ограничения на величину спроса на материалы: X2 - X1 ≤ 1; X1 ≤ 3. Таким образом получаем математическую модель задачи: · Найти максимум следующей функции: F = 4000X2 + 3000X1 · При ограничениях вида: 2X2 + 3X1 ≤ 7; 3X2 + 2X1 ≤ 9; X2 – X1≤ 1; X1 ≤ 3; X2 ≥0,≥ 0. 2. Переменные задачи X2 ИX1 поместим в ячейках С3 и С4. Целевая функция находится в ячейке С6 и содержит формулу: = 4000 * С4 + 3000 * С3 Ограничения на задачу расположим в диапазоне ячеек С8:D11. 3. Воспользуемся командой Сервис - Поиск решения, вводим необходимые данные для рассматриваемой задачи (установка данных в окне поиск решения приведена на рис 12. Результат работы по поиску решения помещен на рис 13-14.
Рис 12. Рабочий лист MSExcel для решения задачи планирования производства материалов.
Рис.13. Рис.14. Установка необходимых параметров задачи планирование материалов в окне Поиск решения.
Рис. 14. Результат расчета надстройки Поиск решения.
Описание отчетов о решении задачи. 1. Отчет по результатам приведен на рис.15. Таблица целевая ячейка выводит сведения о целевой функции; таблица изменяя ячейки показывает значения переменных, полученных в результате решения задачи; таблица ограничения отображает результаты оптимального решения для ограничений и для граничных условий. В поле формула приведены зависимости, которые были выведены в окно Поиск решения, в поле разница – величины используемого материала. Если материал используется полностью, то в поле статус указывается связанное, при неполном использовании материала в этом поле указывается несвязан. 2. Отчет по устойчивости приведен на рис. 16. – в таблице изменяемые ячейки приводится результат решения задачи. В таблице ограничения выводятся занчения для ограничений, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение. 3. Отчет по пределам приведен на рис. 17. – в отчете показано в каких пределах может изменяться количество материалов, вошедших в оптимальное решение, при сохранении структуры оптимального решения; приводятся значения переменных в оптимальном решении, а также нижние и верхние пределы изменения значений переменных, здесь также указаны значения целевой функции при выпуске данного типа продукции на верхнем и нижнем пределах.
Рис. 15.
Рис. 16.
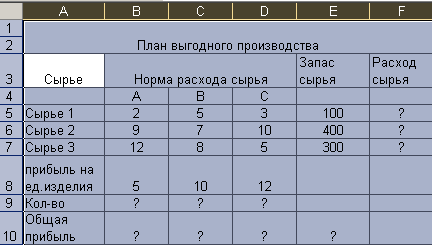
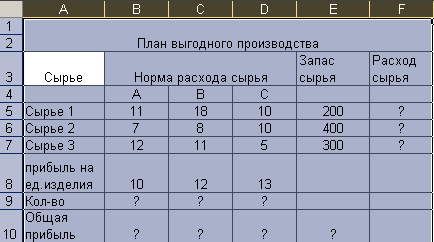
Рис. 17. ЗАДАНИЕ 1. Фирма производит несколько видов продукции из одного и того же сырья - А, В, С. Реализация продукции А дает прибыль 10 руб., В – 15руб. и С – 0 руб. на единицу изделия. Продукцию можно производить в любых количествах, поскольку известно, что сбыт обеспечен, но ограничены запасы сырья. Необходимо определить, какой продукции и сколько надо произвести, чтобы общая прибыль от реализации была максимальной. С помощью Поиска решения определите, какой продукции и сколько нужно произвести, чтобы общая прибыль была максимальной. Нормы расхода сырья на производство продукции каждого вида приведены. Создать отчеты о решении задачи (отчет по результатам, отчет по устойчивости, отчет по пределам).
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
ЗАДАНИЕ 2 Вариант 1 С двух пунктов сбора А Математическая формулировка задачи. Обозначим Х Х
Математическая формулировка задачи. Обозначим Х Х Ограничения по возможностям сборных пунктов А Х Целевая функция минимизации транспортных затрат имеет вид: F = 20 ∙ Х Для решения задачи в Excel необходимо правильно поместить математическую модель по ячейкам электронной таблицы при этом целесообразно придерживаться таблицы заполнения ячеек (Табл2). Сформировать описания отчетов о решении задачи.
Вариант 2 С двух пунктов сбора А
Математическая формулировка задачи. Обозначим Х Х Ограничения по возможностям сборных пунктов А Х Целевая функция минимизации транспортных затрат имеет вид: F = 15 ∙ Х Для решения задачи в Excel необходимо правильно поместить математическую модель по ячейкам электронной таблицы, при этом целесообразно придерживаться таблицы заполнения ячеек (Табл2). Сформировать описания отчетов о решении задачи.
Вариант 3 С двух пунктов сбора А
Математическая формулировка задачи. Обозначим Х Х Ограничения по возможностям сборных пунктов А Х Целевая функция минимизации транспортных затрат имеет вид: F = 18 ∙ Х Для решения задачи в Excel необходимо правильно поместить математическую модель по ячейкам электронной таблицы, при этом целесообразно придерживаться таблицы заполнения ячеек (Табл2). Сформировать описания отчетов о решении задачи.
Вариант 4 С двух пунктов сбора А
Математическая формулировка задачи. Обозначим Х Х Ограничения по возможностям сборных пунктов А Х Целевая функция минимизации транспортных затрат имеет вид: F = 25 ∙ Х Для решения задачи в Excel необходимо правильно поместить математическую модель по ячейкам электронной таблицы при этом целесообразно придерживаться таблицы заполнения ячеек (Табл2). Сформировать описания отчетов о решении задачи.
Вариант 5. С двух пунктов сбора А
Математическая формулировка задачи. Обозначим Х Х Ограничения по возможностям сборных пунктов А Х Целевая функция минимизации транспортных затрат имеет вид: F = 18 ∙ Х Для решения задачи в Excel необходимо правильно поместить математическую модель по ячейкам электронной таблицы при этом целесообразно придерживаться таблицы заполнения ячеек (Табл2). Сформировать описания отчетов о решении задачи.
Вариант 6 С двух пунктов сбора А
Математическая формулировка задачи. Обозначим Х Х Ограничения по возможностям сборных пунктов А Х Целевая функция минимизации транспортных затрат имеет вид: F = 15 ∙ Х Для решения задачи в Excel необходимо правильно поместить математическую модель по ячейкам электронной таблицы, при этом целесообразно придерживаться таблицы заполнения ячеек (Табл2). Сформировать описания отчетов о решении задачи.
Вариант 7 С двух пунктов сбора А
Математическая формулировка задачи. Обозначим Х Х Ограничения по возможностям сборных пунктов А Х Целевая функция минимизации транспортных затрат имеет вид: F = 18 ∙ Х Для решения задачи в Excel необходимо правильно поместить математическую модель по ячейкам электронной таблицы при этом целесообразно придерживаться таблицы заполнения ячеек (Табл2). Сформировать описания отчетов о решении задачи.
Вариант 8 С двух пунктов сбора А
Математическая формулировка задачи. Обозначим Х Х Ограничения по возможностям сборных пунктов А Х Целевая функция минимизации транспортных затрат имеет вид: F = 15 ∙ Х Для решения задачи в Excel необходимо правильно поместить математическую модель по ячейкам электронной таблицы при этом целесообразно придерживаться таблицы заполнения ячеек (Табл2). Сформировать описания отчетов о решении задачи.
Вариант 9. С двух пунктов сбора А
Математическая формулировка задачи. Обозначим Х Х Ограничения по возможностям сборных пунктов А Х | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 X1
X1  – суточный обьем производства материала А;
– суточный обьем производства материала А;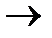














 и А
и А 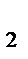 требуется развести личный состав по трем объектам В
требуется развести личный состав по трем объектам В  , В
, В  , В
, В  таким образом, чтобы транспортные издержки были минимальны. Имеются данные о стоимости перевозок между сборными пунктами и объектами (табл.2). Также известно, что на пункте сбора А
таким образом, чтобы транспортные издержки были минимальны. Имеются данные о стоимости перевозок между сборными пунктами и объектами (табл.2). Также известно, что на пункте сбора А  количество личного состава, перевозимого с пункта сбора I на объект J. Тогда критерием полного обеспечения В
количество личного состава, перевозимого с пункта сбора I на объект J. Тогда критерием полного обеспечения В  + Х
+ Х  ≥ 100, Х
≥ 100, Х 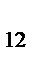 + Х
+ Х  ≥ 120, Х
≥ 120, Х  + Х
+ Х  ≥ 220.
≥ 220.


