
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическая группировка предприятийСодержание книги
Поиск на нашем сайте
Таблица 7
Аналитическая группировка позволяет визуально установить наличие и направление связи. По итогам проведенной группировки можно сделать вывод, что связь между объемом производимой продукции и себестоимостью продукции есть. Такой вывод можно сделать на основании данных табл. 7, сравнив 3 и 4 колонки: с увеличением объема производимой продукции средние затраты на производство единицы продукции снижаются. Результат произведенной группировки совпал с предположением, сделанным на основании теоретического, качественного, анализа. Интенсивность связи при аналитической группировке устанавливается с помощью специализированных показателей. Ряды распределения Ряд распределения представляет собой простейший вид структурной группировки. Для ряда распределения система показателей исчерпывается одним показателем — численность группы. В зависимости от признака, положенного в основу группировки (качественный или количественный), различают атрибутивный и вариационный ряды распределения. Атрибутивный ряд распределения применяется в том случае, когда простая группировка проводится по качественному показателю. Число градаций признака определяет число групп (табл. 8).
Распределение сотрудников фирмы по уровню образования Таблица 8
Частота — частота появления данного значения варианты в совокупности. Сумма всех частот будет характеризовать число единиц совокупности или ее размеры. Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Например, в табл. 8 ряд распределения характеризуется и частотой и частостью. В зависимости от значений, которые принимает варианта, различают дискретный вариационный и непрерывные ряды распределения. В том случае, если признак может принимать любые значения в заданном промежутке, имеем непрерывный ряд распределений. Этот непрерывный ряд распределений может быть представлен в виде интервалов. Примеры дискретных рядов распределения: Распределение семьи по числу детей. Распределение студентов по баллу, полученному на экзамене. Распределение рабочих по тарифному разряду. Примеры интервального ряда распределения: Распределение рабочих по стажу. Распределение рабочих по уровню заработной платы. С помощью рядов распределения решаются следующие задачи: — характеристика структуры совокупности; — оценка соответствия фактического распределения теоретическому ряду распределения; — наиболее наглядный способ представления рядов распределения — графический. Графиками в статистике называются условные изображения числовых величин и их соотношений в виде различных геометрических образов — точек, линий, плоских фигур и т.п. Система группировок
Статистическая группировка — статистический 1метод, применяемый на втором этапе статистического исследования, основное назначение которого — систематизация данных, полученных в результате статистического наблюдения. Для того чтобы статистическое исследование было полным и давало наиболее полное представление об изучаемом явлении или процессе, оно должно охватывать все существенные стороны рассматриваемого явления. Поэтому вышеизложенные виды группировок, методика их построения могут быть использованы в комплексе. Первоначально проводится типологическая группировка, которая выделяет однокачественные однородные группы. Затем в пределах выделенного типа проводится структурная и факторная группировки. которые дают характеристику типа. Почему необходима система? Всякое явление, процесс имеет множество сторон, множество целей, характеризуется множеством признаков, изменяется в разные периоды времени. При его изучении необходимо решать множество задач. Эта особенность массовых явлений вызывает необходимость систематического подхода к его изучению. Поэтому сложные массовые явления изучаются с помощью систем группировок. Чтобы построить систему группировок, необходимо выполнить некоторые логические и формальные требования. Логические требования: — группировки должны охватывать все. без исключения существенные стороны явления; — система должна включать все виды группировок по решаемым задачам; — группировки не должны противоречить друг другу. Формальные требования: — группировки по качественным признакам должны предшествовать группировкам по количественным признакам; — таблицы в системе группировок должны иметь стабильную нумерацию; — результативные признаки в группировках должны быть сопоставимы, то есть измерены в одинаковых единицах; — интервалы группировок должны быть неизменными из года в год. Выводы: 1. Статистическая группировка является методом обобщения статистических данных, основой для правильного исчисления статистических показателей. 2. Статистическая группировка — основа сводки статистических данных. 3. В соответствии с решаемыми задачами различают три вида группировок: типологическую, структурную, аналитическую. 4. Сложные массовые явления изучаются с помощью систем группировок.
Задание 1.3.1. Отметьте правильные ответы: 1. Для выявления взаимосвязи между признаками проводят группировку: а) типологическую; б) вариационную; в) аналитическую. 2) В том случае, если группы образованы по одному признаку, группировка: а) простая; б) многомерная. 3) Атрибутивный ряд распределения — это: а) простая группировка, построенная по качественному признаку, который характеризуется численностью группы; б) простая группировка, построенная по количественному признаку.
Задание 1.3.2. Отметьте правильные ответы: 1. Выделите атрибутивные группировочные признаки: а) возраст человека; б) национальность; в) доход сотрудника фирмы; г) форма собственности. 2. При построении группировки по атрибутивному признаку задача определения числа групп решается: а) по усмотрению исследователя; б) число групп соответствует числу градаций признака. 3. При проведении группировки по количественному признаку при решении задачи определения числа групп учитывается: а) вариация признака; б) объем совокупности; в) вариация признака и объем совокупности. 4. Аналитическая группировка чаще всего проводится по признаку: а) факторному: б) результативному. 5. Для каких признаков интервалы задаются следующим образом: 15—25; 26—30; 31—35: 36—40 и т.д.? а) дискретных; б) непрерывных. 6. Границы интервалов обозначены следующим образом: 20—25; 25—30. В какую группу следует отнести единицу совокупности, значение признака которой соответствует 25? а) в 1 группу (20—25); б) во 2 группу (25—30). 7. Специализированные интервалы применяются при построении группировки: а) простой; б) многомерной.
Задание 1.3.3. Отметьте правильные ответы: Частота — это: а) численность отдельных вариант или групп вариационного ряда; б) численность отдельных вариант или групп вариационного ряда, выраженная в процентах к итогу Частость — это: а) численность отдельных вариант или групп вариационного ряда; б) численность отдельных вариант или групп вариационного ряда, выраженная в процентах к итогу.
Задание 1.3.4. В результате проведения контрольной работы в группе из 25 человек получен следующий ряд оценок: 4, 4, 4, 5, 5, 2, 3, 3, 4, 5, 3, 3, 5, 5, 4, 2, 5, 3, 2. 4, 4, 4, 3, 5, 5. Постройте ряд распределения студентов по оценкам, полученным за контрольную работу, результаты представьте в таблице. Определите варианту и частоту.
Варианта: Частота: Библиографический список основной 1. Общая теория статистики: Учебник / Под ред. чл.-корр. РАН И.И.Елисеевой.— М.: Финансы и статистика, 2000.—С. 118—155. 2. Практикум по теории статистики: Учеб. пособие / Под ред. проф. Р.А.Шмойловой.— М.: Финансы и статистика, 1999.— С. 26—45. 3. Статистика: Курс лекций / Под ред. В.Г.Ионина.— Новосибирск: Издательство НГАЭиУ, 1996.— С. 29—38. 4. Теория статистики: Учебник / Под ред. проф. Р.А.Шмойловой.— М., 1996. дополнителъныи 1. Лунвев В.В. Юридическая статистика: Учебник.— М.: Юристъ, 1999.— С. 154—175. 2. СавюкЛ.К. Правовая статистика: Учебник.— М.: Юристъ, 1999.— С. 266—288.
ТЕМА 1.4. СТАТИСТИЧЕСКИЕ ВЕЛИЧИНЫ
1.4.1. Виды статистических величин. 1.4.2. Понятие средней величины. Виды средних величин. 1.4.3. Правила выбора формы средних величин. 1.4.4. Средняя арифметическая, способы расчета. 1.4.5. Структурные средние величины. Виды статистических величин
При определении предмета статистики отмечалось, что статистика рассматривает количественную сторону массовых общественных явлений, то есть любое явление общественной жизни рассматривается при помощи различных статистических величин. Все используемые в статистике величины можно разделить на абсолютные, относительные и средние. Абсолютные величины бывают индивидуальные и суммарные. В том случае, если абсолютная величина характеризует размер единицы совокупности — это индивидуальная величина, например: возраст, пол отдельно взятого человека. Если абсолютная величина характеризует всю совокупность в целом или группу единиц совокупности, то говорят о суммарной относительной величине. Индивидуальные величины получают непосредственно в результате статистического наблюдения из первичных документов. Суммарные получают либо путем подсчета единиц совокупности, либо путем суммирования отдельных значений признака по совокупности. Всегда абсолютные величины именованы, имеют размерность. В зависимости от социально-экономической сущности явления, их физических свойств они могут быть выражены в натуральных, стоимостных или трудовых единицах измерения. Натуральные единицы характеризуют размер явления физических мер: объема, веса. Разновидность натурального учета — условно-натуральный метод. Его идея — агрегирование абсолютных величин, имеющих сходные потребительские свойства. Например. Различные виды органического топлива переводятся в условное топливо с теплотой 29,3 мДж/кг, мыло разных сортов — в мыло с 40% содержанием жирных кислот, консервы разного объема — в условные консервные банки объемом 353,4 куб, см. Перевод в условные единицы осуществляется с помощью переводных коэффициентов, которые рассчитываются как отношение потребительских свойств отдельных разновидностей продуктов к их эталонному значению. Стоимостной метод — наиболее универсальный — применяется для интегральной характеристики конечных результатов деятельности функционирования экономики. В стоимостном измерении рассчитывается валовой внутренний продукт — центральный показатель, характеризующий конечные результаты деятельности экономики. На уровне предприятия в стоимостной оценке измеряется объем производимой продукции, общие затраты на производство продукции, выручка от реализации продукции и т.д. Трудовой метод позволяет соизмерить затраты труда (чел/дни, чел/часы, численность работающих). Вторая форма выражения статистических данных — относительные величины, которые, как правило, используются при решении аналитических задач и рассчитываются на основании абсолютных величин. При расчете относительных величин в числителе находится так называемая величина сравнения, а в знаменателе — база сравнения. Каждую относительную величину можно представить следующим образом:
где y1 — сравниваемая величина. В статистике она называется «отчетная» или «текущая» величина, либо «фактическая»; у0 — база сравнения — величина, с которой проводится сравнение, называется базисной. При расчете относительных величин необходимо выполнять условия сопоставимости числителя и знаменателя по следующим направлениям: — по кругу объектов, то есть показатель должен быть рассчитан, например, по одному и тому же предприятию; — по территории; — по времени (по моменту регистрации); — по методике расчета; — по ценам. Все используемые в практике статистические величины можно подразделить на следующие виды: — относительная величина планового задания; — относительная величина выполнения плана; — относительная величина динамики; — относительная величина структуры; — относительная величина координации; — относительная величина интенсивности; — относительная величина сравнения; В зависимости от размера относительные величины могут быть измерены в коэффициентах (разах), процентах, промилле (тысячная часть числа). Например, если относительная величина динамики равна 2, то говорят, что значение показателя увеличилось в два раза, при изменении этого показателя на 0,1 говорят об увеличении значения на 10%. Все без исключения хозяйственные единицы планируют свою деятельность на определенный период и сравнивают полученные результаты с плановыми значениями. На основании этих значений рассчитывают относительную величину планового задания и выполнения плана. Относительная величина планового задания:
где упп — планируемая величина данного показателя; yбаз — уровень этого показателя, достигнутый в предплановый период. Эта величина не является статистической величиной (в строгом смысле слова), так как не имеет вариаций. Однако рассматривается в статистике ввиду того, что образует замкнутую систему с двумя следующими показателями. Относительная величина выполнения плана:
где yфакт — фактический уровень достигнутого плана. Относительная величина планового задания характеризует, сколько процентов составляет планируемая величина от достигнутого уровня, в то время как относительная величина выполнения плана показывает процент, который составляет фактически достигнутый уровень, от плановой величины. Относительная величина динамики объединяет два предыдущих показателя и характеризует динамику показателя, то есть сколько процентов составляет текущее значение по отношению к базисному, или во сколько раз изменилось значение показателя в отчетном периоде по сравнению с предыдущим
Между приведенными показателями существует взаимосвязь:
Относительная величина структуры характеризует долю данной группы или данной единицы в общем объеме совокупности:
где хi — значение i -ой группы (признака);
п — число групп (признаков). Пример рассчета отраслевой структуры совокупности малых предприятий России (табл. 1).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.121.241 (0.01 с.) |

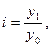
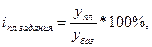

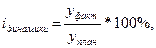
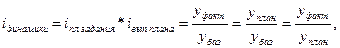
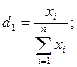
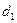 — доля, удельный вес i -ой группы (признака);
— доля, удельный вес i -ой группы (признака); — объем совокупности;
— объем совокупности;


