
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородное дифференциальное уравнение первого порядка
2.3.1. Однородное дифференциальное уравнение вида:
Дифференциальное уравнение (2.3.1) называется однородным, если функция f(x,y) является однородной функцией нулевого измерения. Функция f(x,y) называется однородной функцией нулевого измерения, если выполняется тождество: f(λx,λy)= f(x,y), где λ – константа. Для решения однородного дифференциального уравнения применяют подстановку:
где u – функция от х. Подставив соотношения (2.3.2) в исходное уравнение (2.3.1), получим уравнение с разделяющимися переменными:
Разделяя переменные и интегрируя, получим общее решение. Пример 4. Найти общее решение уравнения:
Решение. Уравнение (2.3.4) является однородным, так как функция
Представим исходное уравнение (2.3.4) в виде:
Сделав подстановку (2.3.2), получим уравнение с разделяющимися переменными:
Разделяем переменные и интегрируем:
Сделав обратную замену, получим общее решение:
2.3.2. Однородное дифференциальное уравнение вида:
Дифференциальное уравнение (2.3.5) называется однородным, если функции P(x,y) и Q(x,y) являются однородными функциями одного измерения. Функция f(x,y) называется однородной функцией n -го измерения, если выполняется тождество: f(λx,λy)= λnf(x,y), где λ – константа. Для решения однородного дифференциального уравнения (2.3.5) применяют подстановку:
Подставив соотношения (2.3.6) в исходное уравнение (2.3.5), получим уравнение с разделяющимися переменными:
Разделяя переменные и интегрируя, получим общее решение. Пример 5. Найти общее решение уравнения
Решение. Уравнение (2.3.8) является однородным, так как функции
Сделаем подстановку (2.3.6), получим уравнение с разделяющимися переменными:
Сократим уравнение на х 2 и преобразуем:
Разделяем переменные и интегрируем:
Подставим y/x вместо u и преобразуем общее решение:
Линейное дифференциальное уравнение первого порядка Линейное дифференциальное уравнение первого порядка имеет вид:
где функция Q(x) называется правой частью линейного уравнения. Искомая функция у и ее производная входят в уравнение в виде линейной комбинации.
Если правая часть Q(x)= 0, то уравнение (2.4.1) называется линейным однородным или линейным уравнением без правой части:
Уравнение (2.4.2) решается путем разделения переменных. Если правая часть Q(x)≠ 0, то уравнение (2.4.1) называется линейным неоднородным или линейным уравнением с правой частью. Для решения уравнения этого типа существует несколько способов: метод Бернулли, метод Лагранжа (метод вариации произвольных постоянных) и др. Метод Бернулли Для решения линейного неоднородного дифференциального уравнения применяют подстановку:
где u и v – функции от х. Подставим соотношения (2.4.3) в исходное уравнение (2.4.1):
Вынесем u за скобку:
Выражение в скобке приравняем к нулю:
Соотношение (2.4.5) является линейным однородным дифференциальным уравнением, которое решается путем разделения переменных:
Подставим (2.4.6) в (2.4.4):
Соотношение (2.4.7) является дифференциальным уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, находим функцию u:
В итоге общее решение имеет вид:
Пример 6. Найти общее решение уравнения:
Решение. Сделав подстановку (2.4.3), получим:
Квадратную скобку приравняем к нулю и решим полученное уравнение с разделяющимися переменными:
Разделяем переменные и интегрируем:
Получаем:
Сокращаем на х, разделяем переменные и интегрируем:
Находим общее решение у:
Пример 7. Найти общее решение уравнения:
Решение. Сделав подстановку (2.4.3), получим:
Квадратную скобку приравняем к нулю и решим полученное уравнение с разделяющимися переменными:
Разделяем переменные и интегрируем:
Получаем:
Функцию
Сокращаем на
Находим общее решение у:
Пример 8. Найти общее решение уравнения:
Решение. Сделав подстановку (2.4.3), получим:
Квадратную скобку приравняем к нулю и решим полученное уравнение с разделяющимися переменными:
Разделяем переменные и интегрируем:
Получаем:
Функцию v=х подставляем в соотношение (2.4.10):
Сокращаем на х, разделяем переменные и интегрируем:
Находим общее решение у:
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.172.249 (0.028 с.) |
 (2.3.1)
(2.3.1) (2.3.2)
(2.3.2) (2.3.3)
(2.3.3) (2.3.4)
(2.3.4) является однородной функцией нулевого измерения:
является однородной функцией нулевого измерения: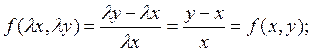
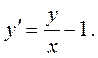
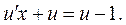



 или
или 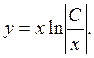
 (2.3.5)
(2.3.5)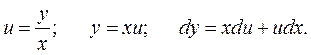 (2.3.6)
(2.3.6) (2.3.7)
(2.3.7) (2.3.8)
(2.3.8) и
и 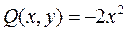 являются однородными функциями второго измерения:
являются однородными функциями второго измерения: ;
;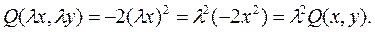


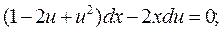

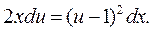


 или
или 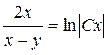 .
. (2.4.1)
(2.4.1) (2.4.2)
(2.4.2) (2.4.3)
(2.4.3)
 (2.4.4)
(2.4.4) (2.4.5)
(2.4.5)


 (принимаем С =0). (2.4.6)
(принимаем С =0). (2.4.6) (2.4.7)
(2.4.7)
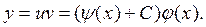



 (2.4.8)
(2.4.8)

 или
или  Функцию v=х подставляем в соотношение (2.4.8):
Функцию v=х подставляем в соотношение (2.4.8):



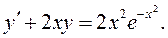


 (2.4.9)
(2.4.9)

 или
или 
 подставляем в соотношение (2.4.9):
подставляем в соотношение (2.4.9):
 , разделяем переменные и интегрируем:
, разделяем переменные и интегрируем:






 (2.4.10)
(2.4.10)







