
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обыкновенные дифференциальные уравнения первого порядкаСтр 1 из 3Следующая ⇒
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Методические указания к практическим занятиям по дисциплине «Математика»
Составители: Егорова Ю.Б. Мамонов И.М. Никулина Т.А.
МОСКВА 2014
Обыкновенные дифференциальные уравнения первого порядка: Методические указания к практическим занятиямпо дисциплине «Математика»/ Ю.Б. Егорова, И.М. Мамонов, Т.А. Никулина. М.: МАТИ, 2014. – 25 с.
ÓЕгорова Ю.Б., Мамонов И.М., Никулина Т.А., составление, 2014
Ó МАТИ, 2014
ОСНОВНЫЕ ПОНЯТИЯ Дифференциальным уравнением первого порядка называется уравнение, содержащее неизвестную (искомую) функцию у(х), независимую переменную х и первую производную у' или дифференциалы первого порядка dx и dy. Если искомая функция является функцией одной независимой переменной, то дифференциальное уравнение называется обыкновенным. Если независимых переменных несколько, то дифференциальное уравнение называется уравнением в частных производных. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Обыкновенное дифференциальное уравнение первого порядка символически можно записать в общем виде следующим образом:
Дифференциальное уравнение первого порядка, разрешенное относительно первой производной, имеет вид:
Процесс нахождения решения дифференциального уравнения является интегрирование. Решением дифференциального уравнения называется всякая функция, которая обращает его в тождество. Дифференциальное уравнение первого порядка имеет бесчисленное множество решений, которые можно представить в виде функции Функция, получающаяся из общего решения при конкретном значении постоянной С, называется частным решением. Частное решение находится при помощи задания начальных условий: у(х=х0)=у0, где х0, у0 – конкретные числа. Задача отыскания частного решения дифференциального уравнения, удовлетворяющего начальному условию, называется задачей Коши. Практически задачу Коши решают следующим образом: находят общее решение, затем в него подставляют начальные условия, определяют конкретное значение произвольной постоянной С и подставляют его в общее решение.
ОСНОВНЫЕ ТИПЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА Метод Бернулли Для решения линейного неоднородного дифференциального уравнения применяют подстановку:
где u и v – функции от х. Подставим соотношения (2.4.3) в исходное уравнение (2.4.1):
Вынесем u за скобку:
Выражение в скобке приравняем к нулю:
Соотношение (2.4.5) является линейным однородным дифференциальным уравнением, которое решается путем разделения переменных:
Подставим (2.4.6) в (2.4.4):
Соотношение (2.4.7) является дифференциальным уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, находим функцию u:
В итоге общее решение имеет вид:
Пример 6. Найти общее решение уравнения:
Решение. Сделав подстановку (2.4.3), получим:
Квадратную скобку приравняем к нулю и решим полученное уравнение с разделяющимися переменными:
Разделяем переменные и интегрируем:
Получаем:
Сокращаем на х, разделяем переменные и интегрируем:
Находим общее решение у:
Пример 7. Найти общее решение уравнения:
Решение. Сделав подстановку (2.4.3), получим:
Квадратную скобку приравняем к нулю и решим полученное уравнение с разделяющимися переменными:
Разделяем переменные и интегрируем:
Получаем:
Функцию
Сокращаем на
Находим общее решение у:
Пример 8. Найти общее решение уравнения:
Решение. Сделав подстановку (2.4.3), получим:
Квадратную скобку приравняем к нулю и решим полученное уравнение с разделяющимися переменными:
Разделяем переменные и интегрируем:
Получаем: Функцию v=х подставляем в соотношение (2.4.10):
Сокращаем на х, разделяем переменные и интегрируем:
Находим общее решение у:
Уравнение Бернулли Уравнение Бернулли – это дифференциальное уравнение первого порядка, имеющее вид:
где n ≠0, n ≠1. Для решения уравнения этого типа существует несколько способов: метод Бернулли, метод вариации произвольных постоянных (метод Лагранжа), метод приведения к линейному виду и др.
Пример 10. Найти общее решение уравнения:
Решение. Первый способ решения методом Бернулли. Сделав подстановку (2.4.3), получим:
Квадратную скобку приравняем к нулю и решим полученное уравнение с разделяющимися переменными:
Разделяем переменные и интегрируем:
Получаем:
Функцию
Сокращаем на х, разделяем переменные и интегрируем:
Находим общее решение у:
Второй способ решения методом Лагранжа. Приравняем правую часть уравнения к нулю:
Решим полученное уравнение с разделяющимися переменными:
Разделяем переменные и интегрируем:
Получаем:
Пусть постоянная С=С(х) – некоторая функция от х. Тогда:
Найдем производную:
Подставим (2.5.3) и (2.5.4) в исходное уравнение:
Подставим (2.5.5) в общее решение (2.5.3):
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Дайте определение дифференциального уравнения первого порядка. 2. Дайте определения общего и частного решения дифференциального уравнения первого порядка. 3. Как называется задача нахождения частного решения? 4. Как можно найти частное решение из общего? 5. Перечислите типы дифференциальных уравнений первого порядка. 6. Каким методом решаются дифференциальные уравнения с разделенными и разделяющимися переменными? 7. Каким методом решается однородное дифференциальное уравнение первого порядка? 8. Каким методом решается линейное однородное дифференциальное уравнение первого порядка? 9. Какими методами решается линейное неоднородное дифференциальное уравнение первого порядка? 10. Какими методами решается уравнение Бернулли?
ЛИТЕРАТУРА 1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов,т.1.– М: Наука. –2005, 526с. 2. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, т.2. – М: Наука. –2005, 575с. 3. Сборник задач по математике для ВТУЗов. Под ред. Ефимова А.В., Поспелова А.С. М. Ф-м.лит. – 2003, ч.2, 432 с. (http://www.rusfolder.com) 4. Данко П.Е., Попов А.Г., Кожевникова Высшая математика в упражнениях и задачах., т.2, М: Высшая школа – 2003, 415с. (http://www.diary.ru). 5. Агафонов С.А., Герман А.Д., Муратова Т.А. Дифференциальные уравнения. – М.: МГТУ имени Н.Э. Баумана, 2000. - 348 с.
ОГЛАВЛЕНИЕ
Введение…………………………..………………………………………………3 1. Основные понятия………………………………………..…….........................3 2. Основные типы дифференциальных уравнений первого порядка …..……4 2.1. Дифференциальное уравнение с разделенными переменными………4 2.2. Дифференциальное уравнение с разделяющимися переменными…….5 2.3. Однородное дифференциальное уравнение первого порядка……….…….7 2.4. Линейное дифференциальное уравнение первого порядка……………….11 2.5. Уравнение Бернулли ……………………………………………………….. 18 Контрольные вопросы………………………………………….......................... 24 Литература……….………………………………………………………………. 23
Юлия Борисовна Егорова Игорь Михайлович Мамонов Татьяна Анатольевна Никулина
ПЕРВОГО ПОРЯДКА
Редактор
Уч.-изд.л. - Тираж экз. Зак. Издательский центр МАТИ
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Методические указания к практическим занятиям по дисциплине «Математика»
Составители: Егорова Ю.Б. Мамонов И.М. Никулина Т.А.
МОСКВА 2014
Обыкновенные дифференциальные уравнения первого порядка: Методические указания к практическим занятиямпо дисциплине «Математика»/ Ю.Б. Егорова, И.М. Мамонов, Т.А. Никулина. М.: МАТИ, 2014. – 25 с.
ÓЕгорова Ю.Б., Мамонов И.М., Никулина Т.А., составление, 2014
Ó МАТИ, 2014
ОСНОВНЫЕ ПОНЯТИЯ Дифференциальным уравнением первого порядка называется уравнение, содержащее неизвестную (искомую) функцию у(х), независимую переменную х и первую производную у' или дифференциалы первого порядка dx и dy. Если искомая функция является функцией одной независимой переменной, то дифференциальное уравнение называется обыкновенным. Если независимых переменных несколько, то дифференциальное уравнение называется уравнением в частных производных. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Обыкновенное дифференциальное уравнение первого порядка символически можно записать в общем виде следующим образом:
Дифференциальное уравнение первого порядка, разрешенное относительно первой производной, имеет вид:
Процесс нахождения решения дифференциального уравнения является интегрирование. Решением дифференциального уравнения называется всякая функция, которая обращает его в тождество. Дифференциальное уравнение первого порядка имеет бесчисленное множество решений, которые можно представить в виде функции Функция, получающаяся из общего решения при конкретном значении постоянной С, называется частным решением. Частное решение находится при помощи задания начальных условий: у(х=х0)=у0, где х0, у0 – конкретные числа. Задача отыскания частного решения дифференциального уравнения, удовлетворяющего начальному условию, называется задачей Коши. Практически задачу Коши решают следующим образом: находят общее решение, затем в него подставляют начальные условия, определяют конкретное значение произвольной постоянной С и подставляют его в общее решение.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.232 (0.081 с.) |
 или
или 
 .
. Эта совокупность решений называется общим решением.
Эта совокупность решений называется общим решением. (2.4.3)
(2.4.3)
 (2.4.4)
(2.4.4) (2.4.5)
(2.4.5)


 (принимаем С =0). (2.4.6)
(принимаем С =0). (2.4.6) (2.4.7)
(2.4.7)
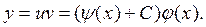



 (2.4.8)
(2.4.8)

 или
или  Функцию v=х подставляем в соотношение (2.4.8):
Функцию v=х подставляем в соотношение (2.4.8):



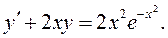


 (2.4.9)
(2.4.9)

 или
или 
 подставляем в соотношение (2.4.9):
подставляем в соотношение (2.4.9):
 , разделяем переменные и интегрируем:
, разделяем переменные и интегрируем:






 (2.4.10)
(2.4.10)




 (2.5.1)
(2.5.1)


 (2.5.2)
(2.5.2)

 или
или 
 подставляем в соотношение (2.5.2):
подставляем в соотношение (2.5.2):

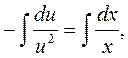






 или
или 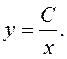
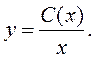 (2.5.3)
(2.5.3) (2.5.4)
(2.5.4)


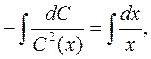

 (2.5.5)
(2.5.5)



