
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Эйлера интегрирования однородных линейных систем с постоянными коэффициентами.Содержание книги
Поиск на нашем сайте
Однородной линейной системой дифференциальных уравненийназывается система уравнений вида:
y Î Rn, x Î [a,b], где A(x) - квадратная матрица размера nхn, элементы которой непрерывны на интервале [a,b] функции. Любое решение системы уравнений (6) можно продолжить на весь интервал [a,b]. Множество всех решений a всех решений системы (6), определенных на [a,b], является линейным пространством. Линейное пространство a всех решений однородной линейной системы изоморфно фазовому пространству Rn этой системы. Метод Эйлера заключается в следующем. Решение системы (6) находится в виде:
Функция (15) является решением системы (6), если
где С1, С2, …, Сn – произвольные числа. Для случая кратных корней решение системы принимает вид
где Pi(x)-полиномы степени не выше, чем (к-1), имеющих в совокупности к произвольных коэффициентов. Так что среди коэффициентов этих полиномов к коэффициентов являются произвольными, а оставшиеся к Если для k - кратного собственного значения
Если для собственного значения
Чтобы найти векторы а0, а1, …, аk-m, надо подставить выражение (19) в систему (6). Приравняв коэффициенты подобных членов в левой и правой частях системы, получим уравнение для нахождения векторов а0, а1, …, аk-m. Если среди собственных чисел матрицы А имеются комплексные числа, то указанным выше методом строится соответствующее такому собственному числу решение системы (6) через комплексные функции. Чтобы выразить решение через действительные функции (в случае действительной матрицы), надо воспользоваться тем, что вещественная и мнимая части комплексного решения, соответствующего собственному числу Таким образом, в случае, когда собственные числа являются комплексными, решение представимо в виде:
Умножим транспонированную фундаментальную матрицу решений на вектор свободных коэффициентов [C1, C2, C3, C4] и получим вектор общего решения исходной системы
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.115.222 (0.007 с.) |

 (6)
(6)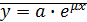 , где а = [ a1, a2, …, an ] (15)
, где а = [ a1, a2, …, an ] (15) – собственное значение матрицы А, а а – собственный вектор этой матрицы, соответствующей числу
– собственное значение матрицы А, а а – собственный вектор этой матрицы, соответствующей числу  1,
1,  2, …,
2, …, 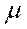 n матрицы А попарно различны и a1, a2, …, an соответствующие собственные векторы этой матрицы, то общее решение системы уравнений (6) определяется формулой:
n матрицы А попарно различны и a1, a2, …, an соответствующие собственные векторы этой матрицы, то общее решение системы уравнений (6) определяется формулой: (16)
(16) (17)
(17) n-k выражаются через них. Для отыскания коэффициентов полиномов подставим решение (17) в исходную систему уравнений, приравняем коэффициенты при одинаковых функциях. Решим систему по отношению к (k
n-k выражаются через них. Для отыскания коэффициентов полиномов подставим решение (17) в исходную систему уравнений, приравняем коэффициенты при одинаковых функциях. Решим систему по отношению к (k  (18)
(18)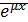 , т.е. в виде:
, т.е. в виде: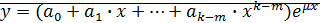 (19)
(19) , где
, где 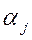 - комплексные числа.
- комплексные числа. или
или
 Каждой паре корней соответствует 2 линейно-независимых решения:
Каждой паре корней соответствует 2 линейно-независимых решения:


 При подстановке решения в исходную систему получается верное равенство, из этого следует, что решение найдено верно
При подстановке решения в исходную систему получается верное равенство, из этого следует, что решение найдено верно 


