
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Системы эконометрических уравнений ⇐ ПредыдущаяСтр 5 из 5
1. Предварительно ознакомиться с теоретическим материалом: Л1 [Гл. 4], Л2 [Гл. 3], Л3 [Гл. 9]. Примеры с решениями. Пример 1. Изучается модель вида:
Данная система из трех уравнений содержит три зависимые, эндогенные ( В структурной форме (СФМ) для нахождения параметров модели Обычно для определения структурных коэффициентов модели СФМ преобразуется в приведенную форму модели (ПФМ).
Параметры приведенной формой модели Структурные формы модели могут быть – идентифицируемые; – неидентифицируемые; – сверхиндетифицируемые. Для того чтобы СФМ была идентифицируема, необходимо чтобы каждое уравнение системы было идентифицируемо. В этом случае число параметров СФМ равно числу параметров приведенной формы. Если хотя бы одно уравнение СФМ неидентифицируемо, то вся модель считается неидентифицируемой. В этом случае число коэффициентов приведенной формы модели меньше, чем число коэффициентов СФМ. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае можно получить два и более значений одного структурного коэффициента на основе коэффициентов приведенной формы модели. В сверхидентифицируемой модели хотя бы одно уравнение сверхидентифицируемо, а остальные уравнения идентифицируемы. Если обозначить число эндогенных переменных в i -том уравнении СФМ через Н, а число предопределенных переменных, которые содержатся в системе, но не входят в данное уравнение через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила: если D+1 < H – уравнение неидентифицируемо; если D+1 = H – уравнение идентифицируемо; если D+1 > H – уравнение сверхидентифицируемо. Счетное правило является необходимым, но не достаточным условием идентификации. Кроме этого правила для идентифицируемости уравнения должно выполняться дополнительное условие.
Отметим в системе эндогенные и экзогенные переменные, отсутствующие в рассматриваемом уравнении, но присутствующие в системе. Из коэффициентов при этих переменных в других уравнениях составим матрицу. При этом, если переменная стоит в левой части уравнения, то коэффициент надо брать с обратным знаком. Если определитель полученной матрицы не равен нулю, а ранг не меньше, чем количество эндогенных переменных в системе без одного, то достаточное условие индетификации для данного уравнения выполнено. Проверим каждое уравнение системы на выполнение неоходимого и достаточного условия идентификации. В первом уравнении три эндогенных переменных: Для проверки на достаточное условие составим матрицу из коэффициентов при переменных Таблица 1 Матрица, составленная из коэффициентов при переменных
Во втором уравнении две эндогенные переменные: Для проверки на достаточное условие составим матрицу из коэффициентов при переменных Таблица 2 Матрица, составленная из коэффициентов при переменных
Определитель представленной в таблице 2 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и второе уравнение идентифицируемо.
В третьем уравнении три эндогенные переменные: Для проверки на достаточное условие составим матрицу из коэффициентов при переменных Таблица 3 Матрица, составленная из коэффициентов при переменных
При оценивании коэффициентов структурной модели используется ряд методов. Рассмотрим косвенный метод наименьших квадратов (КМНК), который применяется в случае точно идентифицируемой структурной модели. Пример 2. Рассмотрим КМНК на примере следующей идентифицируемой модели, содержащей две эндогенные и две экзогенные переменные:
Для построения модели мы располагаем информацией, представленной в таблице 4. Таблица 4. Фактические данные для построения модели
Структурную модель преобразуем в приведенную форму модели.
где u 1 и u 2 – случайные ошибки. Для каждого уравнения приведенной формы при расчете коэффициентов d можно применить МНК. Для упрощения расчетов можно работать с отклонениями от средних уровней Для нахождения коэффициентов
Таблица 5 Преобразованные данные для построения приведенной формы модели
Подставляя рассчитанные в таблице 5 значения сумм, получим
Решение этих уравнений дает значения d11 = 2,822 и d12 = 0,394. Первое уравнение приведенной формы модели примет вид
Для нахождения коэффициентов d2 k второго приведенного уравнения можно использовать следующую систему нормальных уравнений:
Подставляя рассчитанные в таблице 5 значения сумм, получим
Решение этих уравнений дает значения d21 = 1,668 и d22 = 1,177. Второе уравнение приведенной формы модели примет вид
Для перехода от приведенной формы к структурной форме модели найдем
Подставим это выражение в первое уравнение приведенной модели, найдем структурное уравнение
Таким образом, b 12 = 0,335; a 11 = 2,264. Найдем
Подставим это выражение во второе уравнение приведенной модели, найдем структурное уравнение
Таким образом, b 21 = 0,591; a 22 = 0,944. Свободные члены структурной формы находим из уравнений
Окончательный вид структурной модели
Пример 3. Изучается модель вида:
Требуется: 1. Оценить следующую структурную модель на идентификацию: 2. Исходя из приведенной формы модели уравнений
найти структурные коэффициенты модели. Решение. 1. Модель имеет три эндогенные (у 1, у 2, у 3) и три экзогенные (х 1, х 2, х 3) переменные. Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации. Первое уравнение. Н: эндогенных переменных – 2 (у 1, у 3), отсутствующих экзогенных – 1 (x 2). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в первом уравнении отсутствуют у 2 и x 2. Построим матрицу из коэффициентов при них в других уравнениях системы:
Det A = -l×0 - b 32× a 22 ¹ 0. Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо. Второе уравнение. Н: эндогенных переменных – 3 (y 1, y 2, y 3), отсутствующих экзогенных – 2 (x 1, x 3). Выполняется необходимое равенство: 3=2+1, следовательно, уравнение точно идентифицируемо. Д: во втором уравнении отсутствуют x 1 и x 3. Построим матрицу из коэффициентов при них в других уравнениях системы:
Det A = a 11 ×a 33 - a 31 ×a 13 ¹ 0. Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо. Третье уравнение. Н: эндогенных переменных – 2 (y 2, y 3), отсутствующих экзогенных – 1 (x 2). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в третьем уравнении отсутствуют y 1 и x 2. Построим матрицу из коэффициентов при них в других уравнениях системы:
Det A = -l× a 22 - b 21 × 0 ¹ 0.
Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо. Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов. 2. Вычислим структурные коэффициенты модели: 1) из третьего уравнения приведенной формы выразим х 2 (так как его нет в первом уравнении структурной формы):
Данное выражение содержит переменные y 3, x 1 и x 3, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x 2 в первое уравнение приведенной формы модели (ПФМ):
2) во втором уравнении СФМ нет переменных x 1 и x 3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа: Первый этап: выразим x 1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует x 3, которого нет в СФМ. Выразим x 3 из третьего уравнения ПФМ:
Подставим его в выражение x 1:
Второй этап: аналогично, чтобы выразить x 3 через искомые y 1, y 3, и x 2, заменим в выражении x 3 значение x 1 на полученное из первого уравнения ПФМ:
Следовательно,
Подставим полученные x 1 и x 3 во второе уравнение ПФМ:
3) из второго уравнения ПФМ выразим x 2, так как его нет в третьем уравнении СФМ:
Подставим полученное выражение в третье уравнение ПФМ:
Таким образом, СФМ примет вид
Тема 4. Временные ряды 1. Предварительно ознакомиться с теоретическим материалом: Л1 [Гл. 5], Л2 [Гл. 4], Л3 [Гл. 6]. Примеры с решениями. Пример 1. МОДЕЛЬ С АДДИТИВНОЙ КОМПОНЕНТОЙ Приведены данные о количестве продукции, проданной компанией в течение последних 13 кварталов.
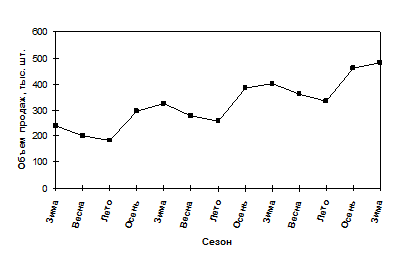
Требуется: 1. Построить аддитивную модель временного ряда. 2. Сделать прогноз на 2 квартала вперед. Решение. 1. Проанализируем данные и попробуем обнаружить тенденцию. Если устойчивая тенденция действительно существует, то построенную модель можно будет использовать для прогнозирования объема продаж в следующих кварталах. Для этого построим график временного ряда (см. рис.).
Из графика следует, что возможен возрастающий тренд, содержащий сезонные колебания. Так объемы продаж в зимний период (1 и 4) значительно выше, чем в летний (2 и 3). Сезонная компонента практически не изменилась за последние три года. Тренд показывает, что в среднем объем продаж возрос с 240 тыс. шт. в 2003 г. до 480 тыс. шт. в 2006 г., однако увеличение сезонных колебаний не наблюдалось. Этот факт свидетельствует в пользу модели с аддитивной компонентой
2. Расчет сезонной компоненты. Для исключения влияния сезонной компоненты используют метод скользящей средней, суть которого заключается в нахождении среднего арифметического значения параметра за m моментов времени
Для рассмотренных данных об объемах продаж проведем следующие расчеты. 1. Производя скольжение по значениям квартальных продаж из колонки 2, вычислим сумму продаж за каждые четыре квартала и внесем ее в колонку 3 табл. 1. 2. Вычислим скользящую среднюю за каждые 4 квартала (колонка 4). 3. Поскольку усредненные данные, внесенные в колонку 3, относятся не к конкретному кварталу, а к моменту времени между двумя кварталами (например, между апрелем-июнем и июлем-сентябрем 2003 г.), то необходимо получить центрированную скользящую среднюю для каждой пары значений из колонки 4. Полученные значения относятся к конкретным кварталам, начиная с июля-сентября 2003 года, их вносят в колонку 5. Таким образом, величины из колонки 5 являются десезонализированными средними значениями за квартал. 4. Сезонную компоненту, содержащую остаток, рассчитывают по формуле 5. Используя данные за все годы, вычисляют среднее значение для каждого квартала, что позволит уменьшить значения ошибок (табл. 2). 6. Средние оценки сезонной компоненты корректируются, путем увеличения или уменьшения некоторых из них на одно и то же число, таким образом, чтобы их общая сумма была равна 0. Корректирующий фактор рассчитывают следующим образом: сумма оценок сезонных компонент делится на 4. Аналогичная процедура применима при определении сезонной вариации за любой промежуток времени. Например, если в качестве сезонов рассматриваются не кварталы, а дни недели, то устранения влияния сезонной компоненты рассчитывают скользящую среднюю, но уже не по четырем, а по семи точкам. Эта скользящая средняя представляет собой значение тренда в середине недели, т.е. в четверг. Поэтому в этом случае необходимость в центрировании отпадает. 3. Десезонализация данных при расчете тренда. Десезонализация исходных данных заключается в вычитании скорректированных сезонных компонент (последняя строка табл. 2) из фактических значений данных за каждый квартал, т.е. Нанесем значения новых оценок тренда из колонки 4 на график исходных данных, что еще раз подтвердит существование явного линейного тренда. Определим уравнение линии тренда методом наименьших квадратов
Таблица 1
Таблица 2
Таблица 3
4. Расчет ошибок Из (1) следует, что величина ошибки равна
Значение T найдем из уравнения (2), а S из табл. 2. Результаты расчета представлены в табл. 4. Таблица 4
Столбец 5 можно использовать при расчете среднего абсолютного отклонения MAD (mean absolute deviation) и средней квадратической ошибки MSE (mean square error):
где В нашем случае ошибки достаточно малы и составляют от 0,2% до 2,2%. Тенденция, выявленная по фактическим данным, достаточно устойчива и позволяет получить хорошие краткосрочные прогнозы. 5. Прогнозирование по аддитивной модели. Прогнозные значения рассчитываются по формуле
где x – номер квартала, на который дается прогноз, T – значение тренда, рассчитанное по (2), S (x) – сезонная компонента, составляющая в январе-марте 42,6, в апреле-июне – 20,7, в июле-сентябре – 62,0, в октябре-декабре – 40,1. Например, прогноз на апрель-июнь 2006 г. (x = 14) имеет вид
Можно предположить, что ошибка прогноза будет приблизительно 0,3-2,2% в соответствии с рассчитанными ошибками модели, но чем более отдаленным является период упреждения, тем меньшей оказывается обоснованность прогноза. Пример 2. МОДЕЛЬ С МУЛЬТИПЛИКАТИВНОЙ КОМПОНЕНТОЙ В некоторых временных рядах значение сезонной компоненты не является константой, а представляет собой определенную долю трендового значения, т.е. значение сезонной компоненты увеличивается с возрастанием значений тренда. Например, рассмотрим график следующих данных об объемах продаж.
Объем продаж этого продукта так же, как и в предыдущем примере, подвержен сезонным колебаниям, и значения его в зимний период выше, чем в летний. Однако размах вариации фактических значений относительно линии тренда постоянно возрастает. Такую ситуацию можно представить с помощью модели с мультипликативной компонентой
1. Расчет сезонной компоненты. Отличие расчета сезонной компоненты для мультипликативной модели от аддитивной модели заключается лишь в том, что в колонку 6 вписываются коэффициенты сезонности (аналог оценок сезонной компоненты в аддитивной модели)
Сезонные коэффициенты представляют собой доли тренда, поэтому принимают, что их сумма должна равняться количеству сезонов в году, т.е. 4, а не нулю, как в аддитивной модели. Если бы в качестве сезонов рассматривались дни недели, то эта сумма равнялась бы 7. Если сумма вычисленных коэффициентов Таблица 1
Таблица 2
2. Десезонализация данных при расчете тренда. Десезонализация данных производится по формуле
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.119.148 (0.123 с.) |
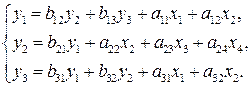
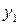 ,
, 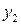 ,
,  ) и четыре независимые, экзогенные (
) и четыре независимые, экзогенные (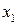 ,
, 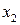 ,
, 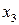 ,
,  ) переменные.
) переменные. и
и  (называемых также структурными коэффициентами модели), простой МНК неприменим.
(называемых также структурными коэффициентами модели), простой МНК неприменим.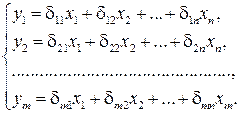
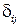 могут быть оценены по методу наименьших квадратов. По этим параметрам затем можно рассчитать структурные коэффициенты модели
могут быть оценены по методу наименьших квадратов. По этим параметрам затем можно рассчитать структурные коэффициенты модели 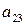 и
и 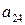 , соответственно. В третьем уравнении эти переменные отсутствуют, т.е. коэффициенты при них равны нулю. Так как вторая строка матрицы состоит из нулей, определитель матрицы равен нулю. Значит, достаточное условие не выполнено, и первое уравнение нельзя считать идентифицируемым.
, соответственно. В третьем уравнении эти переменные отсутствуют, т.е. коэффициенты при них равны нулю. Так как вторая строка матрицы состоит из нулей, определитель матрицы равен нулю. Значит, достаточное условие не выполнено, и первое уравнение нельзя считать идентифицируемым.




 и
и  (
( и
и  – средние значения). Преобразованные таким образом данные таблицы 4 сведены в таблицу 5. Здесь же показаны промежуточные расчеты, необходимые для определения коэффициентов
– средние значения). Преобразованные таким образом данные таблицы 4 сведены в таблицу 5. Здесь же показаны промежуточные расчеты, необходимые для определения коэффициентов  .
.

 .
.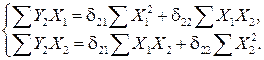

 .
. .
.
 .
. .
.
 .
. ,
, .
.


 .
. Þ
Þ – первое уравнение СФМ:
– первое уравнение СФМ: .
. .
. ;
;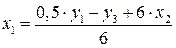 .
.
 .
.
 – второе уравнение СФМ.
– второе уравнение СФМ. .
.
 – третье уравнение СФМ.
– третье уравнение СФМ.
 . (1)
. (1) .
.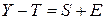 и вносят в колонку 6.
и вносят в колонку 6. (табл. 3).
(табл. 3). . (2)
. (2)


 .
. и
и  .
. и
и  – это фактическое и прогнозное значение в момент времени t.
– это фактическое и прогнозное значение в момент времени t. (тыс. шт. за квартал),
(тыс. шт. за квартал), ,
, тыс. шт.
тыс. шт.
 .
. .
. не равна 4, то их корректируют, путем умножения соответствующей доли на
не равна 4, то их корректируют, путем умножения соответствующей доли на  .
.



