
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы, действующие на ВУ к БП ствольной артиллерии.Содержание книги
Поиск на нашем сайте
При рассмотрении действия ВУ помимо четкого представления об его устройстве необходимо знать и учитывать силы, действующие на взрыватель на различных этапах его эксплуатации. При служебном обращении на взрыватель могут действовать вибрационные и ударные перегрузки, возникающие в процессе транспортировки изделий или случайных падений БП с ВУ при погрузочно-разгрузочных работах. Эти перегрузки можно разделить на две группы. К первой группе относятся вибрационные и импульсные перегрузки, ко второй - ударные и квазистатические. Под вибрационными понимаются перегрузки, возникающие во ВУ при транспортировке вследствие колебаний (вибраций) упругой системы транспорта. Различают свободные и вынужденные колебания упругой системы транспорта. Первые возникают и затухают после каждого одиночного воздействия апериодической внешней силы, например, при столкновении колес транспорта с неровностями почвы. Вынужденные колебания появляются при периодическом действии сил, источником которых могут являться неуравновешенность вращающихся частей мотора, периодическое чередование дорожных неровностей (стыков рельс) и другие подобные причины. Вибрационные перегрузки, возникающие при указанных колебаниях, изменяются по определенному периодическому закону, а их частоты совпадают с соответствующими частотами свободных и вынужденных колебаний упругой системы транспорта. К импульсным перегрузкам относятся перегрузки, появляющиеся в результате относительного движения (подскоков) укупорки с ВУ и последующего соударения ее с платформой транспорта. Эти перегрузки имеют характер одиночных кратковременных импульсов, чередующихся с вибрационными перегрузками. Импульсные перегрузки могут появляться и при совместном движении укупорки и платформы в тех случаях, когда при наездах на препятствия амплитуда свободных колебаний подрессоренного транспорта превышает допустимую, ввиду чего имеет место удар о жесткие ограничители хода. Ударные перегрузки появляются при наездах автомашин на большие выбоины дороги, при падениях укупорки с ВУ во время погрузочно-разгрузочных работ. Эти перегрузки являются, по существу, импульсными, но характеризуются относительно малой повторяемостью и большой величиной. Поэтому их целесообразно выделить в отдельную группу. Квазистатические перегрузки появляются при различных маневрах (виражах и горках самолета, торможении поезда и т. д.) и характеризуются сравнительно большой длительностью действия, измеряемой секундами и десятками секунд, т. е. являются как бы статическими. Подытоживая все выше сказанное можно утверждать, что в служебном обращении на ВУ могут действовать вибрационные и ударные перегрузки длительностью в несколько миллисекунд и перегрузки амплитудой не более 100 единиц. При проектировании ВУ, а также при их подготовке к приемо-сдаточным испытаниям они подвергаются специальным испытаниям. Прежде всего, эти испытания должны оценивать функционирование ВУ в процессе действия вибрационных и импульсных перегрузок, возникающих при транспортировке. Они обязательны для всех ВУ. В настоящее время такие испытания проводят на приборе «Сит», вибростендах (типа ВП-70) или непосредственно возкой на автомобиле. Цель ударных испытаний состоит в воспроизведении ударных перегрузок. Данному виду испытаний подвергаются также все виды ВУ. Они проводятся путем сброса укупорок ВУ с определенных высот на различные преграды. Иногда для этой цели используются специальные ударные стенды, например «Массет» или «Пур». Силы, действующие на ВУ при выстреле (рис. 3.4) Во время движения по каналу ствола артиллерийского орудия на детали ВУ в общем случае действуют четыре силы инерции: - осевая сила инерции - центробежная сила - касательная (тангенсальная) сила инерции - кориолисова сила инерции Осевая силы инерции
где
где С учетом площади полей нарезов
где Для вычисления коэффициента фиктивности В. Е. Слухоцким предложено приближенное выражение
где
Отсюда где Из этого выражения видно, что сила инерции Характер изменения сил Максимальное значение силы инерции имеет место при
Коэффициент Для современных артиллерийских систем значения По этим же соображениям для взрывателей в гранатометах, реактивных системах и крупных БП (с гораздо меньшим значением После вылета снаряда из канала ствола давление пороховых газов на его дно быстро падает. Также быстро в этот период (период последействия пороховых газов) убывает осевое ускорение снаряда и осевая сила инерции, действующая на детали взрывателя. В большинстве случаев действием осевых сил инерции на деталь ВУ в этот период, в виду его кратковременности, можно пренебречь. Однако в тех случаях, когда осевые силы инерции в период последействия вредно влияют на поведение взрывателя, действительную кривую
где
справедлива при
Во вращающихся БП возникает центробежная сила
Между угловой скоростью БП и его поступательной скоростью
где Наибольшее значение
Подставляя в исходное выражение для
На рис. 3.6 показан характер нарастания скорости БП
Введя коэффициент центробежной взводимости
для
Численное значение
Следовательно, для большинства ВУ к артиллерийским БП можно в качестве предохранительных механизмов использовать центробежные - ЦПМ. Последние по сравнению с ИПМ обеспечивают большую безопасность (позднее взведение), но ограниченную область применения. Во время движения БП по каналу орудия его угловая скорость непрерывно возрастает, и возникают силы инерции от касательных ускорений.
Так как то Таким образом, касательная сила инерции пропорциональна ускорению поступательного движения
В существующих орудиях крутизна нарезов а эксцентриситет
Таким образом, при выстреле касательная сила Однако в ряде случаев касательная сила инерции Касательная сила инерции Рассмотренные выше силы Наконец следует отметить, что перечисленные силы В противном случае возникает еще одна сила - к ориолисова сила инерции К. Она вызывается кориолисовым (поворотным) ускорением детали и равна (рис. 3.7)
где Очевидно, если деталь относительно БП не движется ( сила равна 0. Она равна нулю и в случае перемещения детали вдоль или параллельно оси БП ( Чтобы найти направление силы K при Следует отметить, что в тех случаях, когда скорость При вылете снаряда из канала ствола давление пороховых газов на дно снаряда быстро падает и вместе с ним падает до 0 и сила S. Центробежная же сила некоторое время еще сохраняет за дульным срезом свое максимальное значение, а затем начинает относительно медленно уменьшаться в связи с торможением БП в воздухе. Это уменьшение ориентировочно можно определить по эмпирической формуле И. А. Слезкина
где L,D,G- соответственно длина, калибр и сила тяжести БП; V -текущее значение скорости БП. На траектории под действием силы сопротивления воздуха БП тормозится и появляется отрицательное ускорение. Соответствующая сила инерции (сила набегания
В наибольшей степени эта сила влияет на ударники инерционного действия и может вызвать их преждевременное срабатывание. Для устранения этого применяются контрпредохранители. Как известно, БП на траектории совершает нутационное и прецессионное колебательные движения. В результате этого появляется осевая сила инерции (сила нутации), определяемая углом нутации В зависимости от степени износа канала ствола сила нутации может изменяться в широких пределах, достигая максимального значения при начальных углах нутации порядка 20 градусов (соответственно перегрузка - несколько сотен единиц). В общем случае вращающийся снаряд движется в воздухе весьма сложным образом. Центр масс снаряда перемещается по криволинейной пространственной кривой. При этом его ось вращается вокруг центра масс, а сам снаряд вращается вокруг оси симметрии. Рассмотрим более простой случай, когда центр масс снаряда движется прямолинейно и равномерно. Пусть ось снаряда совершает относительно касательной к траектории (вектора Для упрощения выкладок можно исходить из того, что снаряд находится в движущемся воздушном потоке и центр масс неподвижен. Проследим за движением детали взрывателя, закрепленной в точке А снаряда на его оси симметрии на расстоянии
где
Угловая скорость Центробежная сила
а нормальная составляющая сила
Таким образом, при постоянных значениях составляющей силы нутации, или просто радиальной силой. Случай регулярной прецессии снаряда на практике встречается редко. Обычно и угол нутации Нутация снаряда, т. е. колебания его оси в плоскости нутации с угловой скоростью
Складывая силы
Сила нутации
Легко видеть, что при положительном ускорении говоря, сила Кроме рассмотренных сил, связанных угловыми скоростями и угловыми ускорениями оси снаряда, возникает еще одна сила инерции. Дело в том, что деталь, расположенная в т. А, одновременно участвует в двух движениях. С одной стороны, она вращается вокруг касательной к траектории (вектора скорости Результирующая радиальная сила N выйдет из плоскости нутации. Величину ее можно определить из выражения
Так как взрыватель с большой скоростью вращается относительно вектора силы Таким образом, в результате вращения оси снаряда вокруг своего центра масс возникают осевая сила инерции Приведенные зависимости сил инерции от параметров вращательного движения снаряда справедливы, если его центр масс движется равномерно и прямолинейно, а центр масс инерционной детали расположен по оси симметрии снаряда. Известно несколько методов экспериментального определения сил инерции, вызванных колебательным движением снаряда с большими углами нутации Известно, что головные взрыватели, снабженные инерционными ударниками, при стрельбе из сильно изношенных стволов (2 и 3 категории износа) могут преждевременно действовать на траектории. Причиной траекторных разрывов является сила нутации, перемещающая ударник с капсюлем по направлению к жалу (ВУ РГМ-2). Если инерционный ударник весом Однако такой упрощенный подход к вопросу о силах нутации, действующих во время полета снаряда, неправилен. Дело в том, что ударник под действием силы нутации небольшой величины в состоянии сдеформировать контрпредохранитель с сопротивлением, превосходящим силу нутации в несколько раз. Это вытекает из того, что между жестким предохранителем и инерционным ударником имеется некоторый зазор. Следовательно, деформация носит динамический характер, в связи с чем, принятый выше статический расчет неправилен. Кроме того, сила нутации является периодически действующей, вызывающей постепенную деформацию контрпредохранителя. Следующий способ измерения силы нутации основан на экспериментальных стрельбах по картонным щитам, когда в каждом щите снаряд вырубает отверстие. По длине этого отверстия можно составить представление об угле нутации д, а по его положению об угле прецессии Недостаток этого метода связан с тем, что этим способом можно определить силы нутации лишь на начальном участке траектории, хотя значительные силы нутации действуют и на конечном участке. Последнее обстоятельство очень важно при проектировании и отработке ВУ к корректируемым БП. Поэтому на кафедре СМ-5 разработан метод их определения с помощью специальных датчиков [10]. Для этой цели применяются акселерографы с часовой разверткой времени, а также телеметрический метод измерения, позволяющий с помощью радиопередатчика, установленного в снаряде, и приемной части, расположенной на земле, зафиксировать период изменения силы нутации и ее величину в функции времени. Помимо силы набегания и силы нутации к преждевременным срабатываниям могут привести и метеорологические факторы, действующие на мембрану головного взрывателя при встрече с каплями дождя, хлопьями снега и крупинками града. Особо важно это при проектировании и отработке ВУ к высокоскоростным зенитным и авиационным БП, т. е. необходимо разрабатывать так называемые всепогодные ВУ. Прежде всего, нужно оценить величину этих дестабилизирующих факторов. Данные о них весьма ограничены. Подобные явления принято рассматривать как процесс мгновенного удара о неподвижную мембрану капли, имеющей скорость, равную скорости движения снаряда. В результате удара капли может произойти деформация мембраны и срабатывание ударного механизма. Последнее возможно, если кинетическая энергия капли (или нескольких капель), встречаемых мембраной взрывателя, больше энергии необходимой для деформации мембраны, преодоления сопротивления контрпредохранителя и воспламенения капсюля. Очевидно, что энергия капли в момент удара о мембрану зависит не только от скорости капли, но и от ее массы. На основании экспериментальных исследований, проведенных НИИ «Поиск» (г. Санкт-Петербург), можно сделать вывод, что при проектировании ВУ, безопасных при стрельбе в дождь, необходимо исходить из предположения о встрече мембраны ВУ с каплями дождя диаметром 2-4 мм. Представляет интерес вопрос о числе соударений мембраны взрывателя с подобными каплями дождя за время полета БП. Если задаться определенным процентным распределением капель дождя по диаметрам, интенсивностью дождя и скоростью падения капель, то по ориентировочному расчету взрыватель, имеющий мембрану диаметром 12 мм, на расстоянии 5 км может встретить 30-40 капель диаметром 2-4 мм. Выше отмечалось, что процесс взаимодействия мембраны с каплей дождя рассматривается как вяление мгновенного удара. В связи с этим, время, в течение которого происходит удар, считается равным нулю и в расчет не принимается. Отсюда вытекает, что определить силу реакции Величины кинетической энергии дождевых капель диаметром 2-4 мм при скоростях БП от 500 до 1200 м/сек приведены в таблице 3.1. Для надежного инициирования KB нужна энергия, не превышающая 0,1 Дж; для прорыва стальной мембраны толщиной 0,13 мм - 0,2-0,3 Дж, для преодоления сопротивления пружинного предохранителя, например, ВУ РГМ-6 - 0,1 Дж. Таким образом, для срабатывания ударного механизма средней чувствительности требуется кинетическая энергия, измеряемая величиной порядка 0,4-0,5 Дж. Сопоставив эту энергию с данными приведенной таблицы, можно видеть, насколько трудно обеспечить несрабатывание ВУ при прохождении снарядом зоны дождя, которая ведет себя в этом случае как твердое тело. Попытки устранить преждевременное срабатывание ВУ путем утолщения мембраны положительного результата не дали из-за ухудшения при этом чувствительности ВУ. Предпринимаемые в настоящее время поиски конструктивного решения задачи обеспечения безопасности ВУ при стрельбе в дождь основаны на использовании разницы в физике процесса удара об одиночные капли и о сплошную преграду. Во всепогодном ВУ (рис. 3.10) мембрана заменена колпачком конической формы толщиной 0,3-0,35 мм с неподвижной центральной частью. Чтобы взрыватель сработал, необходимо обжать колпачок по его боковой поверхности и переместить толкатели 2 в сторону ударника 3, обеспечивающего накол KB 5. Необходимое обжатие колпачка возможно только при ударе о сплошную преграду, а не об отдельные дождевые капли. В последнем случае составляющая сила капли, перпендикулярная стенке колпачка, недостаточна для срабатывания ВУ. Перегрузка, действующая на ВУ при встрече с преградой, определяется физико-механическими свойствами преграды, скоростью и углом встрече с ней БП. В среднем и по уровню, и по продолжительности она сопоставима с перегрузкой, которую испытывает ВУ при выстреле. Эта перегрузка равна отношению сопротивления преграды Сопротивление грунта проникновению БП с головной частью цилиндрической формы можно найти по методу Сагомоняна А.Я. в предположении, что трение о преграду боковой поверхности снаряда не оказывает заметного влияния на силу
где
Площадь
где через
Интегрируя с помощью ЭВМ уравнение движения в преграде БП массой М
Сила сопротивления преграды при соударении БП с водой, имеющего оживальную головную часть
где
где
Силу сопротивления преграды при соударении с броней можно рассчитать по формуле
где
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.45.187 (0.016 с.) |

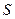 , вызываемая ускорением поступательного движения БП и направленная в сторону, противоположную его движению;
, вызываемая ускорением поступательного движения БП и направленная в сторону, противоположную его движению; , обуславливаемая вращением БП вокруг своей оси;
, обуславливаемая вращением БП вокруг своей оси; , возникающая в связи с изменением угловой скорости БП и направленная по касательной к окружности, образованной вращением центра масс детали ВУ, в сторону, обратную направлению вращения БП;
, возникающая в связи с изменением угловой скорости БП и направленная по касательной к окружности, образованной вращением центра масс детали ВУ, в сторону, обратную направлению вращения БП;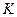 , действующая на детали ВУ в том случае, если он перемещается относительно корпуса взрывателя.
, действующая на детали ВУ в том случае, если он перемещается относительно корпуса взрывателя.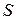 определяется как
определяется как (3.1)
(3.1) - масса детали ВУ,
- масса детали ВУ,  - ускорение поступательного движения БП. Ускорение
- ускорение поступательного движения БП. Ускорение  пороховых газов на дно БП следующей зависимостью
пороховых газов на дно БП следующей зависимостью (3.2)
(3.2) - площадь поперечного сечения канала ствола;
- площадь поперечного сечения канала ствола;  - вес БП;
- вес БП;  коэффициент фиктивности, учитывающий второстепенные работы, производимые пороховыми газами при выстреле.
коэффициент фиктивности, учитывающий второстепенные работы, производимые пороховыми газами при выстреле. (3.3)
(3.3)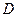 - калибр БП.
- калибр БП.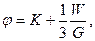 (3.4)
(3.4)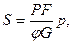 (3.5)
(3.5)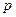 - вес детали ВУ.
- вес детали ВУ.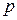 .
.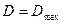 :
: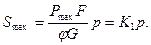 (3.6)
(3.6) показывает во сколько раз максимальное значение осевой силы инерции, действующей на деталь ВУ при выстреле, превосходит ее вес. Этот коэффициент принято называть коэффициентом осевой (линейной) взводимости.
показывает во сколько раз максимальное значение осевой силы инерции, действующей на деталь ВУ при выстреле, превосходит ее вес. Этот коэффициент принято называть коэффициентом осевой (линейной) взводимости.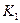 находятся в пределах от нескольких сот единиц (минометы) до нескольких десятков тысяч единиц (малокалиберные зенитные и авиационные пушки). Следовательно, при выстреле из артиллерийских систем инерционные перегрузки во много раз превышают те, которые действуют в служебном обращении. Данное обстоятельство позволяет для подобных ВУ разработать простейшие инерционные предохранительные механизмы (ИПМ), имеющие непрерывное движение взводящейся детали и обеспечивающие безопасность взрывателя в служебном обращении и надежное взведение при выстреле.
находятся в пределах от нескольких сот единиц (минометы) до нескольких десятков тысяч единиц (малокалиберные зенитные и авиационные пушки). Следовательно, при выстреле из артиллерийских систем инерционные перегрузки во много раз превышают те, которые действуют в служебном обращении. Данное обстоятельство позволяет для подобных ВУ разработать простейшие инерционные предохранительные механизмы (ИПМ), имеющие непрерывное движение взводящейся детали и обеспечивающие безопасность взрывателя в служебном обращении и надежное взведение при выстреле. можно заменить прямой, уравнение которой имеет вид:
можно заменить прямой, уравнение которой имеет вид: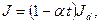 (3.7)
(3.7) ,
, - значение поступательного ускорения у дульного среза. Формула (3.7)
- значение поступательного ускорения у дульного среза. Формула (3.7)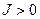 т. е. до момента
т. е. до момента .
. .
. имеется следующая эмпирическая зависимость
имеется следующая эмпирическая зависимость , (3.8)
, (3.8) - крутизна нарезов (длина хода нарезов, выраженная числом калибров
- крутизна нарезов (длина хода нарезов, выраженная числом калибров 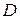 )
)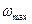 соответствует начальной скорости БП
соответствует начальной скорости БП  :
: , (3.9)
, (3.9) его выражение (3.8), получим
его выражение (3.8), получим . (3.10)
. (3.10) по мере движения снаряда в канале ствола. Максимальное значение центробежной силы имеет место у дульного среза орудия
по мере движения снаряда в канале ствола. Максимальное значение центробежной силы имеет место у дульного среза орудия . (3.11)
. (3.11) , (3.12)
, (3.12)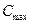 получим следующее выражение
получим следующее выражение .
. показывает, во сколько раз центробежная сила, действующая на деталь ВУ у дульного среза орудия, превосходит ее вес при эксцентриситете
показывает, во сколько раз центробежная сила, действующая на деталь ВУ у дульного среза орудия, превосходит ее вес при эксцентриситете  = 1мм. Для 36-мм авиационных пушек
= 1мм. Для 36-мм авиационных пушек 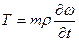 . (3.13)
. (3.13) и
и 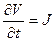 ,
,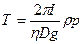 . (3.14)
. (3.14) , как и рассмотренная ранее сила
, как и рассмотренная ранее сила  (3.15)
(3.15)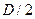 . Следовательно
. Следовательно
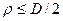 и отношение
и отношение  значительно меньше 0.16. Кроме того касательная сила
значительно меньше 0.16. Кроме того касательная сила  = 0,2), и отношение
= 0,2), и отношение 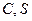 и
и  и начальной скорости
и начальной скорости  . При вычислении указанных сил следует учитывать, что с увеличением температуры окружающего воздуха
. При вычислении указанных сил следует учитывать, что с увеличением температуры окружающего воздуха  и
и 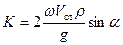 , (3.16)
, (3.16) - скорость перемещения детали относительно БП;
- скорость перемещения детали относительно БП;  - угол между направлением движения детали и осью вращения снаряда.
- угол между направлением движения детали и осью вращения снаряда.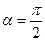 , достаточно вектор скорости
, достаточно вектор скорости  в сторону, обратную направлению вращения БП (рис. 3.7). При
в сторону, обратную направлению вращения БП (рис. 3.7). При 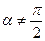 направление силы K можно найтианалогичным образом. С этой целью достаточно вместо вектора
направление силы K можно найтианалогичным образом. С этой целью достаточно вместо вектора  на плоскости, перпендикулярной оси вращения.
на плоскости, перпендикулярной оси вращения. (3.17)
(3.17) - начальная (максимальная) скорость БП;
- начальная (максимальная) скорость БП; ) обуславливает перемещение детали ВУ в направлении движения БП. Эта сила характеризуется коэффициентом набегания
) обуславливает перемещение детали ВУ в направлении движения БП. Эта сила характеризуется коэффициентом набегания
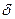 , углом прецессии
, углом прецессии  и скоростями их изменения
и скоростями их изменения  и
и  , a также радиальная сила инерции, зависящая от этих величин и от угловых ускорений нутации
, a также радиальная сила инерции, зависящая от этих величин и от угловых ускорений нутации 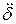 и прецессии
и прецессии  .
. (рис. 3.8). Такое движение называется регулярной прецессией.
(рис. 3.8). Такое движение называется регулярной прецессией. от центра масс. Деталь будет двигаться по окружности. Следовательно, возникает центробежная сила
от центра масс. Деталь будет двигаться по окружности. Следовательно, возникает центробежная сила ,
,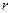 - радиус окружности, равный
- радиус окружности, равный  ;
; - угловая скорость вращения детали.
- угловая скорость вращения детали.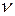 . Скорость вращения плоскости нутации, равная
. Скорость вращения плоскости нутации, равная  к оси снаряда. Проекция ее на ось снаряда равна
к оси снаряда. Проекция ее на ось снаряда равна ,
, .
.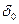 и
и  деталь взрывателя испытывает действие постоянной осевой силы инерции
деталь взрывателя испытывает действие постоянной осевой силы инерции  и радиальной силы
и радиальной силы  , постоянной по величине, но меняющей свое направление по отношению к быстровращающемуся взрывателю. Силу
, постоянной по величине, но меняющей свое направление по отношению к быстровращающемуся взрывателю. Силу  , создает еще одну центробежную силу
, создает еще одну центробежную силу 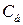 (рис. 3.9), проходящую через точку
(рис. 3.9), проходящую через точку  и лежащую на оси снаряда
и лежащую на оси снаряда .
. , получим выражение для силы нутации
, получим выражение для силы нутации 
 (3.18)
(3.18)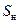 имеет, таким образом, центробежное происхождение. Рассмотрим радиальную силу инерции. Наряду с силой
имеет, таким образом, центробежное происхождение. Рассмотрим радиальную силу инерции. Наряду с силой  , движется затем в обратном направлении. Следовательно, имеет место угловое ускорение
, движется затем в обратном направлении. Следовательно, имеет место угловое ускорение  , направленной перпендикулярно оси снаряда
, направленной перпендикулярно оси снаряда
 (рис. 3.9). Угловая скорость прецессии
(рис. 3.9). Угловая скорость прецессии  . Она направлена по касательной к окружности в точке А. Иначе
. Она направлена по касательной к окружности в точке А. Иначе тоже является радиальной силой, но она направлена под прямым углом к радиальным силам
тоже является радиальной силой, но она направлена под прямым углом к радиальным силам  . Следовательно, возникает кориолисова сила инерции
. Следовательно, возникает кориолисова сила инерции  . Сила
. Сила 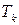 направлена в ту же сторону, что и сила
направлена в ту же сторону, что и сила 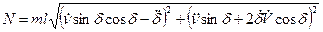 (3.19)
(3.19) , то эта сила непрерывно меняет направление действия по отношению к взрывателю.
, то эта сила непрерывно меняет направление действия по отношению к взрывателю. и взрыватель при этом преждевременно срабатывает на траектории, то возникает предположение, что перегрузки, вызванные силой нутации, достигают величины
и взрыватель при этом преждевременно срабатывает на траектории, то возникает предположение, что перегрузки, вызванные силой нутации, достигают величины  . Так, ВУ РГМ-2 при
. Так, ВУ РГМ-2 при 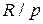 = 290-440 при стрельбе из сильно изношенных орудий дает большое число преждевременных срабатываний.
= 290-440 при стрельбе из сильно изношенных орудий дает большое число преждевременных срабатываний.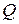 нельзя и можно оперировать лишь интегральными величинами: импульсом силы или кинетической энергией.
нельзя и можно оперировать лишь интегральными величинами: импульсом силы или кинетической энергией.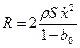 , (3.20)
, (3.20) - плотность грунта;
- плотность грунта; - скорость БП;
- скорость БП; - сжимаемость грунта.
- сжимаемость грунта. цилиндрической поверхности БП и угла
цилиндрической поверхности БП и угла  встречи его с преградой
встречи его с преградой (3.21)
(3.21) обозначен угол
обозначен угол
 при допущении о постоянстве угла
при допущении о постоянстве угла  .
.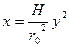 ,
, - радиус цилиндрической части БП;
- радиус цилиндрической части БП;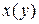 - координаты БП;
- координаты БП; - высота головной части.
- высота головной части. (3.22)
(3.22) - скорость звука в воде;
- скорость звука в воде; - плотность воды.
- плотность воды. , (3.23)
, (3.23) - площадь поперечного сечения цилиндрической части бронебойного снаряда;
- площадь поперечного сечения цилиндрической части бронебойного снаряда; - скорость встречи БП с преградой;
- скорость встречи БП с преградой; - твердость брони;
- твердость брони;


