
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы, действующие на ВУ к реактивным снарядам (РС).
Прежде всего, следует отметить, что характер сил, действующих на эти ВУ в служебном обращении и при встрече с преградой, полностью соответствуют тем выводам, которые были сделаны в 3.2.1., применительно к ВУ артиллерийских БП. Поэтому в данном разделе будут рассмотрены лишь силы, действующие на этапах боевого применения.
Особенности баллистики РС
При реактивном выстреле нарастание скорости снаряда заканчивается в конце активного участка траектории, тогда как ускорение артиллерийских снарядов исчезает в непосредственной близости от орудия. Длина активного участка значительно больше длины ствола орудия, поэтому и силы, действующие на детали ВУ при реактивном и артиллерийском выстреле, существенно отличаются друг от друга. РС имеют по сравнению с артиллерийскими снарядами и минами ряд конструктивных и баллистических особенностей, влияющих на конструкцию отдельных механизмов и всего ВУ в целом. Основной, наиболее общей особенностью является малая величина линейных ускорений с относительно большим временем действия, что затрудняет проектирование предохранительных устройств, обеспечивающих безопасность ВУ как при движении РС на активном участке траектории, так и в процессе служебного обращения. Коэффициент линейной взводимости для РС составляет Угловая скорость РС колеблется в очень широких пределах: от 0 (для оперенных РС - ОРС) до 55000 об/мин (для турбореактивных РС - ТРС). Наконец, скорость РС в конце активного участка траектории колеблется также в широких пределах: от 100 до 1500 м/сек. Отмеченные особенности, очевидно, оказывают значительное влияние на конструкцию ВУ к РС, что и определяет их большое разнообразие. Следует отметить, что первые ВУ к РС не учитывали эти особенности. Поэтому не обеспечивали их боевую эффективность. Так отечественные РС периода II мировой войны снабжались ВУ РГМ, разработанные для артиллерийских БП наземной артиллерии. Первые, специально спроектированные для РС ВУ, появились на вооружении нашей армии лишь в послевоенный период.
Силы, действующие на детали ВУ к ТРС
В зависимости от назначения и устройства ВУ всегда возникает необходимость в проведении или поверочных расчетов с целью выяснения вопросов безопасности и правильного действия его механизмов на полете, при пуске и встрече с преградой, или расчетов, связанных с выбором их параметров, обеспечивающих заданные ТТТ. Подобные расчеты не могут быть проведены без знания законов движения БП на тех или иных участках траектории и знания направления и величины сил, действующих при этом на отдельные элементы ВУ. В связи с этим рассмотрим силы, действующие на детали ВУ к ТРС, на двух основных этапах его движения – на активном и пассивном.
Активный участок траектории ТРС.
В общем случае ТРС на этом участке совершает весьма сложное движение: - поступательно перемещается по траектории; - вращается вокруг собственной продольной оси; - совершает нутационное и прецессионное движения; Во всех этих движениях возникают нормальные, касательные и поворотные ускорения и соответствующие инерционные силы. Для получения простых зависимостей, пригодных для практического использования, примем некоторые допущения, не изменяющие существенно действительного характера движения ТРС на активном участке траектории. В качестве таковых предположим, что снаряд на этом участке движется прямолинейно, а нутационное и прецессионное движения его отсутствуют. Тогда на деталь ВУ будут действовать следующие силы: - сила инерции от линейного ускорения
- центробежная сила
- сила инерции от касательного ускорения
- сила инерции от поворотного (кориолисова) ускорения
где:
Пусть
Тогда уравнение поступательного движения РС на активном участке траектории можно записать в виде (рис.3.12)
а уравнение движения детали в той же системе координат
Из этих уравнений легко найти, что
Так как
то
Тогда сила инерции от линейного ускорения будет равно
Переменный вес снаряда можно записать в виде
где
При этом
где
Расчеты и экспериментальные исследования показывают, что в большинстве случаев весовой секундный расход есть величина постоянная. Поэтому
где Таким образом
Тяга двигателя РС (с твердым топливом) может быть записан в виде
где
После подстановки значений
Как показывают расчеты и экспериментальные исследования влияние силы сопротивления воздуха на скорость ТРС незначительно. Так для снаряда М-8 отрицательная поправка равна ~7 м/сек, что составляет всего 2,2%, для зенитного РС «Тайфун», максимальная скорость которого равна 1100 м/сек, - не превосходит 8%. В связи с этим
Из полученного выражения видно, что сила Максимальная сила инерции будет тогда, когда
Отсюда коэффициент линейной взводимости
В отличие от артиллерийских БП коэффициент линейной взводимости для РС с жидкостным двигателем имеет порядок 5 Перейдем к определению сил, действующих на деталь ВУ к ТРС во вращательном движении снаряда. Для этого воспользуемся уравнением вращательного движения РС
где
Отсюда
Определив величину получим
Следовательно, сила инерции от касательного ускорения, действующая на деталь ВУ, будет равно
Отсюда следует, что сила Так как
где то
Если даже Для детали, взводящихся под действием сил инерции от линейного ускорения, сила
Сила Имея ввиду, что
то можно записать
Отсюда
Таким образом центробежная сила, действующая на деталь ВУ на активном участке траектории, изменяется пропорционально квадрату линейной скорости снаряда, достигая максимального значения в конце активного участка траектории
Отсюда коэффициент
получил название коэффициента центробежной взводимости. Под этим понятием понимается наибольшая центробежная сила, развиваемая единицей веса детали, центр тяжести которой отстает от оси вращения снаряда на расстояние равное единицы. В таблице 3.2 приведены для сравнения значения Для определения сил трения, действующих на подвижные детали, необходимо учитывать также кориолисову силу
Как следует из написанного выражения кориолисова сила равно 0, если: - деталь ВУ не вращается; - деталь ВУ перемещается в плоскости, параллельной оси ВУ [ - ВУ в составе РС не вращается. Максимальное значение она имеет в тех случаях, когда деталь перемещается в плоскости перпендикулярно оси ВУ
Для определения направления действия кориолисовой силы необходимо повернуть вектор относительной скорости детали Полная картина действия всех сил на активном участке движения ТРС должна дополнительно учитывать инерционные силы, возникающие от прецессионного и нутационного движения ТРС. Учет этих сил приводит к необходимости значительного завышения сопротивления контрпредохранителей. Центробежная составляющая этих сил, направленная по оси снаряда, может быть определена по формуле
где
Угловая скорость
где
Таким образом
Пассивный участок траектории ТРС
На пассивном участке траектории двигатель не работает. Поэтому воспользовавшись выражением (3.28), положив в нем
Таким образом, на пассивном участке траектории сила инерции от линейного ускорения меняет свой знак и направлена уже по направлению снаряда. В связи с этим она называется силой набегания, а соответствующий расчетный коэффициент
- коэффициентом силы набегания. Максимальное значение сила набегания имеет в начале пассивного участка, так как сопротивление воздуха в этот момент наибольшее. Затем по мере движения ТРС по траектории сопротивление воздуха все время падает, вследствие уменьшения скорости. Это уменьшение происходит до точки наименьшей скорости, находящейся за вершиной траектории. После этой точки сила набегания вновь начинает возрастать (рис 3.13). Так как всегда Центробежную силу и силу инерции от касательных ускорений можно рассчитать, учитывая закон изменения угловой скорости Так как вектор углового ускорения на траектории меняет свое направление, то меняет свое направление и вектор силы
Силы, действующие на детали ВУ к оперенным реактивным снарядам
Стабилизация ОРС осуществляется с помощью оперения. Поэтому (не учитывая небольшой поворот) на активном и пассивном участках траектории на детали ВУ центробежная сила, кориолисова сила и сила инерции от касательных ускорений действовать не будут. Остается только сила инерции от линейного ускорения, величину которой можно определить по вышеприведенным формулам, положив в них угол Однако при этом существенное значение начинают оказывать силы инерции, возникающие в результате колебаний снаряда около центра тяжести (рис. 3.15)
Как правило, для оперативно-тактических РС, а также для баллистических ракет дальнего действия (БРДД) угол атаки изменяется по закону, близкому к синусоиде (рис.3.16). Следовательно, силы, возникающие в результате этих колебаний, также имеют периодически изменяющий характер. В связи с этим может произойти резкое возрастание амплитуды колебаний механической системы ВУ и нарушение его функционирования, если частота собственных колебаний системы совпадет с частотой внешних периодических воздействий. К таким же результатам может привести наблюдающаяся в реальных условиях полета ракет пульсация реактивной тяги.
Перечисленные факторы обуславливают ужесточение требований к ВУ по вибро- и удароустойчивости, а также вибро- и ударопрочности.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.071 с.) |
 , что во много раз меньше значения
, что во много раз меньше значения  характерного для артиллерийских БП (
характерного для артиллерийских БП ( ). Продолжительность активного участка измеряется долями секунды и секундами. Это существенно больше времени движения снаряда в канале ствола артиллерийского орудия (единицы миллисекунд).
). Продолжительность активного участка измеряется долями секунды и секундами. Это существенно больше времени движения снаряда в канале ствола артиллерийского орудия (единицы миллисекунд). ,
, ,
, ,
, ,
, - масса детали ВУ;
- масса детали ВУ; - угловая скорость вращения БП;
- угловая скорость вращения БП; - относительная линейная скорость БП;
- относительная линейная скорость БП; - абсолютная скорость детали;
- абсолютная скорость детали; - скорость движения БП.
- скорость движения БП. - переменная масса и вес РС;
- переменная масса и вес РС; - переменная тяга ракетного двигателя;
- переменная тяга ракетного двигателя; - сила сопротивления воздуха;
- сила сопротивления воздуха;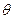 - угол между осью снаряда и осью
- угол между осью снаряда и осью  ;
; - угол между осью снаряда и сопла в плоскости, проходящей через сопло параллельно оси снаряда.
- угол между осью снаряда и сопла в плоскости, проходящей через сопло параллельно оси снаряда. , (3.24)
, (3.24) (3.25)
(3.25)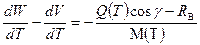 (3.26)
(3.26) ,
, . (3.27)
. (3.27) . (3.28)
. (3.28)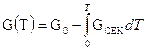 , (3.29)
, (3.29) - начальный (стартовый) вес РС,
- начальный (стартовый) вес РС, - весовой секундный расход топлива.
- весовой секундный расход топлива. ,
, - пассивный вес РС,
- пассивный вес РС, - вес топлива РС.
- вес топлива РС.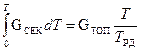 , (3.30)
, (3.30) - полное время работы двигателя (время горения порохового заряда)
- полное время работы двигателя (время горения порохового заряда) . (3.31)
. (3.31) , (3.32)
, (3.32) - давление газов в ракетной камере,
- давление газов в ракетной камере, - суммарная площадь критических сечений сопел.
- суммарная площадь критических сечений сопел. и
и  (3.33)
(3.33) (3.34)
(3.34)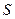 на активном участке траектории изменяется пропорционально давлению
на активном участке траектории изменяется пропорционально давлению  в ракетной камере. Так как давление во времени несколько снижается и в то же время уменьшается масса снаряда, то сила инерции
в ракетной камере. Так как давление во времени несколько снижается и в то же время уменьшается масса снаряда, то сила инерции  . Так как к этому моменту времени успевает сгореть всего (2
. Так как к этому моменту времени успевает сгореть всего (2  3)% веса порохового заряда, то формула (3.34) для
3)% веса порохового заряда, то формула (3.34) для  можно записать
можно записать (3.35)
(3.35) (3.36)
(3.36) , (3.37)
, (3.37) - переменный момент инерции снаряда;
- переменный момент инерции снаряда; - радиус расположения сопел.
- радиус расположения сопел. . (3.38)
. (3.38)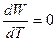 и
и  ,
,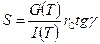 . (3.39)
. (3.39) . (3.40)
. (3.40) изменяется на активном участке траектории РС пропорционально силе
изменяется на активном участке траектории РС пропорционально силе  .
.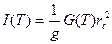 ,
, . (3.41)
. (3.41) , то максимально возможное отношение этих сил не превышает
, то максимально возможное отношение этих сил не превышает  . Так как угол
. Так как угол  , то отсюда следует, что сила инерции от касательного ускорения не превышает (15
, то отсюда следует, что сила инерции от касательного ускорения не превышает (15  , то максимально возможное значение силы трения
, то максимально возможное значение силы трения  по сравнению с силой
по сравнению с силой  , отношение названных сил будет еще меньше. Поэтому влияние силы
, отношение названных сил будет еще меньше. Поэтому влияние силы 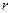 . В отношении деталей, центр тяжести которых лежит на оси вращения РС, действие сил инерции от касательного ускорения сказывается в образовании пары сил, стремящейся повернуть деталь по отношению ВУ и требующей применения специальных устройств для её удержания в тех случаях, когда подобный поворот не допустим. (ВУ Т-5, ВМ-30)
. В отношении деталей, центр тяжести которых лежит на оси вращения РС, действие сил инерции от касательного ускорения сказывается в образовании пары сил, стремящейся повернуть деталь по отношению ВУ и требующей применения специальных устройств для её удержания в тех случаях, когда подобный поворот не допустим. (ВУ Т-5, ВМ-30)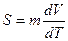
 и приняв вес ракеты и её момент инерции некоторым средним значением
и приняв вес ракеты и её момент инерции некоторым средним значением , (3.42)
, (3.42) (3.43)
(3.43)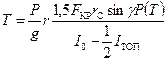 (3.44)
(3.44) (3.45)
(3.45) (3.46)
(3.46) . (3.47)
. (3.47) . (3.48)
. (3.48)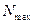 и
и  для некоторых ТРС и артиллерийских снарядов [1], а характер изменения сил
для некоторых ТРС и артиллерийских снарядов [1], а характер изменения сил  на активном участки траектории показан на рис. 3.14.
на активном участки траектории показан на рис. 3.14.
 ];
]; (3.49)
(3.49) на
на  против направления вращения БП.
против направления вращения БП. ,
,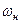 - угловая скорость, обусловленная нутационным и прецессионным движениями БП;
- угловая скорость, обусловленная нутационным и прецессионным движениями БП; - расстояние центра тяжести детали от центра тяжести снаряда.
- расстояние центра тяжести детали от центра тяжести снаряда. (3.50)
(3.50) - максимальное значении нутационных колебаний снаряда;
- максимальное значении нутационных колебаний снаряда; - отношение экваториального момента инерции снаряда к его полярному моменту инерции.
- отношение экваториального момента инерции снаряда к его полярному моменту инерции. (3.51)
(3.51) получим
получим (3.52)
(3.52)
 то сила набегания только в конце (при падении в бездонный колодец), когда
то сила набегания только в конце (при падении в бездонный колодец), когда  получает значение, равное силе тяжести детали
получает значение, равное силе тяжести детали 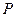 .
. .
. (3.53)
(3.53)


