
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет логики. Понятие логической формыСодержание книги
Поиск на нашем сайте Предмет логики. Понятие логической формы -Слово «логика» происходит от др.греч. «лойос», которое переводится как «понятие», «разум», «рассуждение». Понятие – это мысль, Рассуждение – процесс мышления. Разум тоже имеет отношение к мышлению. То есть логика – наука о мышлении. Науками о мышлениями так же являются психология, физиология высшей нервной деятельности и ряд других. Что же в мышлении составляет предмет изучения логики? Логика изучает формы выражения мыслей и формы развития знания, особые приёмы и методы познания, а так же особые законы мышления. Логическая форма мысли – это её структура, выявляемая в результате частичного отвлечения от смыслов и значений нелогических терминов, входящих в сочетание, выражающее эту мысль. Исторические этапы развития логики. История логики подразделяется на 2 этапа: 1 этап (от возникновения и до середины 19в.). Работы по логике в современной культуре возникают с 5в. до н.э. (труды Демокрита, Платона, Сократа и т.д.), разработки софистов (софизмы – правильные доказательства на основе парадоксов). Аристотель, «отец» логики, разработал основу лгики: - системный метод, - систему умозаключений, - дедуктивный метод, - 3 закона логики. Разработанные логические сведения Аристотель поместил в сборник «Органон». В позднюю античность система Аристотеля дорабатывалась стоиками, Цицероном, Галеном. Они ввели латинскую терминологию, сложные умозаключения. В Средние века учёные Жан Буридан, Уильям Оккам и др. разработали модусы и фигуры силлогизмов. В 16в. (конец Возрождения) логика пришла в упадок. Рамус, один из профессоров Сорбонны, доказал, что все высказывания Аристотеля ложны. В это время во Франции был издан указ о том, что все дисциплины должны преподаваться, опираясь на логику Аристотеля. Во время Варфоломеевской ночи Рамус был убит собственными коллегами и студентами. В нач.17в. в связи с развитием естествознания Френсис Бэкон создаёт «Новый органон», в котором всё основано на индукцию. В 19в. учёные пришли к выводы, что дедукция Аристотеля и индукция Бэкона – 2 части единой логики. Такую логику стали называть традиционной, классической или «белой». - 2 этап (2-ая пол.19в. - …). Ещё в 17в. Лейбниц написал труд «О комбинаторном искусстве». Он положил начало математической или символической логике, которая стала развиваться только спустя 200 лет.Новая логика тесно связана с математикой. По выражению П.С. Парецкого, она представляет собой логику по предмету и математику по методу. В математической логике используются специальный формальный язык и оригинальный метод формализации высказываний.Традиционного логика анализирует формы мысли, символические формы языка. Задача логики состоит в том, чтобы выявить форму мышления.
Язык как знаковая система. Язык – средство по вседневного общения людей, средство общения научной и практической деятельности. Язык позволяет передавать и получать накопленные знания. Практические умения, жизненный опыт, осуществляет процесс обучения и воспитания подрастающего поколения. Язык является знаково – информационной системой, продуктом духовной деятельности чела. Информация передается с помощью знаков языка. Язык это не только средство общения, но и важная составная часть культуры народа. Различаются также искусственные языки. К ним относятся языки математики, символической лог, физики и тд. Знак – материальный предмет выступающий в качестве представителя некоторого другого предмета, св-ва и используемые для приобретения, хранения, переработки и передачи сообщений. Знаки делятся на языковые и неязыковые. К неязыковым относятся: Понятие логического закона. Высказывания, истинные в силу своей логической формы, называются логически истинными. Закон тождества. Закон логики, согласно которому в процессе рассуждения каждое осмысленное выражение (понятие, суждение) должно употребляться в одном и том же смысле. Мысль о предмете должна иметь определённое, устойчивое содержание, сколько бы раз она ни повторялась. Важнейшее свойство мышления - его определённость - выражается данным логическим законом. Закон тождества принято выражать формулой: Отношения между понятиями. Предметы мира находятся друг с другом во взаимосвязи и взаимообусловленности Содержание и объем понятий. Поэтому и понятия, отражающие эти предметы, также находятся в определенных отношениях. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (например, “поэма” и “колодец”; “невоспитанность” и “радуга”), остальные понятия называются сравнимыми. Сравнимые понятия делятся по объему на совместимые (объемы этих понятий совпадают полностью или частично) и несовместимые (их объемы не имеют общих элементов). Типы совместимости: -равнозначность (тождество), перекрещивание, -подчинение (отношение рода и вида) Отношения между понятиями изображают с помощью круговых схем (кругов Эйлера)', где каждый круг обозначает объем понятия. Кругом изображается и единичное понятие. Равнозначными, или тождественными, называются понятия, которые, различаясь содержанием, имеют равные объемы. В них мыслится или одноэлементный класс, или один и тот же класс предметов, состоящий более чем из одного элемента. Примеры равнозначных понятий: 1) “река Нил” и “самая длинная река в мире”; 2) “автор романа “Красное и черное”, “автор романа “Пармская обитель”; 3) “равносторонний прямоугольник”: “ квадрат”; “равноугольный ромб”. Объемы тождественных понятий изображаются кругами, полностью совпадающими. Понятия, объемы которых совпадают частично, т. е. содержат общие элементы, находятся в отношении перекрещивания. Примерами их являются следующие пары: “горожанин” и “садовод”; “студент” и “нумизмат”; “спортсмен” и “учащийся педагогического колледжа”. Они изображаются пересекающимися кругами (рис. 3). В заштрихованной части двух кругов мыслятся учащиеся педагогического колледжа, являющиеся спортсменами или (что одно и то же) спортсмены, являющиеся учащимися педагогического колледжа, в левой части круга А мыслятся учащиеся педагогического колледжа, не являющиеся спортсменами. В правой части круга В мыслятся спортсмены, которые не являются учащимися педагогического колледжаОтношение подчинения (субординации) характеризуется тем, что объем одного понятия целиком включается (входит) в объем другого понятия, но не исчерпывает его. Это отношение вида и рода; А - подчиняющее понятие (“цветок”), В - подчиненное понятие (“чайная роза”) (рис. 3). Содержание и объем понятий. Содержание и объем понятий.
Любое понятие имеет содержание и объем. Содержанием понятия является совокупность характеризующих его предмет существенных признаков, подразумевающихся в данном понятии. Объем понятия составляет совокупность или множество предметов, которое мыслится в понятии. Любое понятие может быть полно охарактеризовано при помощи определения его содержания (иными словами – смысла) и установления предметов, с которыми данное понятие имеет определенные связи. Независимо от сознания человека в окружающем мире существуют различные предметы. Эти предметы характеризуются множеством. Множество может быть конечным или бесконечным. Если количество предметов, входящих в множество, поддается исчислению, множество считается конечным. Если такие предметы не поддаются исчислению, множество называют бесконечным. Необходимо упомянуть об отношениях включения, принадлежности и тождества. Отношение включения – это отношение вида и рода. Множество А является частью или подмножеством множества В, если каждый элемент А есть элемент В. Отражается в виде формулы А є В (множество А входит в множество В). В отношении принадлежности класса принадлежит классу А и записывается как а є А. Отношение тождества подразумевает, что множества А и В совпадают. Это закрепляется как А є В. Содержание понятия называется его интенсиональностью, а его отношение к каким-либо объектам – экстенсиональностью. Интенсиональность понятий. Чаще всего в процессе толкования термина «содержание понятия» его определяют в качестве понятия как такового. В этом случае подразумевается, что содержание понятия есть система признаков, при посредстве которых предметы, содержащиеся в понятии, обобщаются и выделяются из массы других. Из сказанного выше видно, что содержанием понятия является некая информация, содержащая сведения о предметах, явлениях, процессах, входящих в данное понятие. Например, слова «книга» – «книжонка»; «бабка» – «бабушка» – «бабуля» вполне иллюстрируют коннотацию. Экстенсиональность понятий. Любое понятие отражает какой-либо предмет, содержит признаки, характеризующие и отделяющие его от других предметов. Этот предмет всегда связан с другими предметами, которые не входят в содержание данного понятия, однако имеют признаки, частично повторяющие признаки предмета, отраженного в понятии. Эти предметы составляют особую группу. Такую группу можно определить как совокупность объектов, характеризующихся наличием общих признаков, закрепленных хотя бы одним понятием.
11. Определение понятий. Правила определения. Определение – это лог операция которая раскрывает содержание понятия, либо устанавливает значение термина. С помощью определения понятий мы указываем на сущность отраженных в понятии предметов, раскрываем содержание понятия и тем самым отличаем круг определенных предметов от других предметов. Существует 2 вида определения понятий: Реальные – раскрывают сущность предметов (естественный отбор – процесс выживания наиболее приспосабливаемых особей, который ведет к преимуществу сильной особи над другими.); Номинальные – если определенный термин обозначает понятие. (Вещества растворов которые проводят эл ток, назыв электропроводными.) Определение должно быть соразмерным т.е. объем определения понятия должен быть равен объему определенного понятия.
Суждение как форма мышления Мысль, выраженная в форме понятия, сама по себе ещё не есть процесс мышления. Для инициализации мыслительного процесса необходима элементарная логическая форма, каковой является суждение. В суждении выражается отношение между двумя и более понятиями; устанавливается такое отношение, мы и осуществляем элементарный мыслительный акт. Такая форма мышления посредством которой, сочетая понятия, что-либо утверждают или отрицают о реальных вещах и явлениях, называют суждением. Суждения как форма мышления в языке закрепляется и передаётся другим людям с помощью предложения. Например, понятие «Киев» принимаем форму предложения, когда мы утверждаем что его как «Киев – столица Украины»; это и есть мысль, выраженная в форме логического суждения. Суждение – это такая логическая форма, которая может быть истинной или ложной; установление того или другого и являются задачей логики. А подобно В. В подобно А. Для свойства рефлексивности (xRy -+ xRx л yRy ): если суждение xRy истинно, то истинными будут суждения xRx и yRy. Например: а = Ь. а = а и b = b. Для свойства транзитивности (xRy л yRz -* xRz ): если суждение xRy истинно и суждение yRz истинно, то суждение xRz также истинно, Например: К. был на месте происшествия раньше Л. Л. был на месте происшествия раньше М. К. был на месте происшествия раньше М. Таким образом, истинность заключения из суждений с отношениями зависит от свойств отношений и регулируется правилами, вытекающими из этих свойств. В противном случае заключение может оказаться ложным. Так, из суждений «Сергеев знаком с Петровым» и «Петров знаком с Федоровым» не следует необходимого заключения «Сергеев знаком с Федоровым», так как «быть знакомым» не является транзитивным отношением.
А) Разделительно-категорические умозаключения Умозаключения, в которых одна из предпосылок является разделительным суждением, а вторая совпадает с одним из членов дизъюнктивного суждения (1) или отрицает все кроме одного (2). В заключении, соответственно, отрицаются все члены, кроме указанного во второй предпосылке (1), или утверждается пропущенный член (2). Формы правильных модусов разделительно-категорических заключений 1. Утверждающе-отрицающий модус 2. Отрицающе-утверждающий модус
Б) Условные умозаключения Умозаключения, посылки и заключения которых — условные суждения. § Контрапозиция: § Сложная контрапозиция: § Транзитивность: В) Дилеммы Особый вид умозаключений из двух условных суждений и одного разделительного. Виды правильных дилемм: § конструктивные:
(то есть: первая посылка: если A, то C; вторая посылка: если B, то C; третья посылка: A или B; заключение: следовательно, C);
(то есть: первая посылка: если A, то B; вторая посылка: если C, то D; третья посылка: A или C; заключение: следовательно, B или D); § деструктивные:
(то есть: первая посылка: если A, то B; вторая посылка: если A, то C; третья посылка: не B или не C; заключение: следовательно, не A);
(то есть: первая посылка: если A, то B; вторая посылка: если C, то D; третья посылка: не B или не D; заключение: следовательно, не A или не C).
Правила доказательства Для того, чтобы доказательство достигало своей цели, нужно соблюдать некоторые правила, или требования, относящиеся к элементам доказательства. Требования к тезису 1) Тезис должен нуждаться в доказательстве. Бессмысленно пытаться доказывать очевидные вещи, определения понятий, констатации фактов, аксиомы и постулаты. 2) Тезис должен быть ясным и точным. Многие слова естественного языка являются многозначными и расплывчатыми, что обусловливает неясность тезиса. Кроме того, следует иметь в виду, что в качестве тезиса лучше брать частные суждения, а не общие. Частное суждение легче доказать и труднее опровергнуть. 3) Тезис должен оставаться одним и тем же на протяжении всего доказательства. Распространенная ошибка - подмена тезиса. Менее распространенная - потеря тезиса. Требования к аргументам 1) Аргументы должны быть истинными суждениями, причем их истинность должна быть доказана. Нарушение этого требования, связанное с использованием ложного аргумента, называется "основным заблуждением". Ошибка, связанная с использованием, может быть и истинного, но еще не доказанного аргумента носит наименование "предвосхищение основания". 2) Истинность аргументов должна устанавливаться автономно, т. е. независимо от тезиса. При нарушении этого требования мы имеем дело с ошибкой, известной как "круг в обосновании" или "круг в доказательстве". 3) Совокупность аргументов должна быть непротиворечива. Если аргументы противоречат друг другу, то по крайней мере один из них ложен, а ложные аргументы ничего не доказывают. 4) Совокупность аргументов должна быть достаточной для вывода тезиса. Один аргумент почти никогда не дает обоснование тезиса, его доказательная сила мала. Но несколько аргументов, находящихся во взаимной связи, способны создать прочную логическую основу для вывода тезиса. Однако не следует злоупотреблять количеством аргументов. Иногда полагают, что чем больше доводов привлекут к обоснованию своего тезиса, тем лучше. Это не так. Среди неряшливо подобранных аргументов могут оказаться ложные, необоснованные, противоречащие друг другу и даже доказываемому тезису. В таком случае доказательство может рассыпаться. Аргументов должно быть достаточно для вывода тезиса и не более того. Каждый лишний аргумент ослабляет доказательство. Важно не количество аргументов, а их весомость. Требования к демонстрации Это обычные требования к умозаключениям. В повседневной жизни часто случается так, что, высказав некоторые аргументы, человек присоединяет к ним свой тезис с помощью слов: "таким образом", "отсюда можно заключить", "поэтому" и т. п. Однако сами по себе эти слова не создают логической связи между аргументами и тезисом, нужно еще показать, что тезис действительно связан с аргументами определенными видами умозаключений и эти умозаключения корректны. Ошибки, связанные с нарушением правил умозаключений, носят общее название "не следует": тезис логически не вытекает, не следует из аргументов. Виды аналогий. Аналогия - умозаключение о принадлежности предмету определенного признака на основе сходства в признаках с другим предметом. Опровержение. Опровержение — рассуждение, направленное против тезиса с целью установления факта его ложности или недоказанности. Существует несколько приёмов опровержения тезиса. Часто применяемый способ опровержения — вывод следствий, которые противоречат истине. Если одно следствие из утверждения ложно, то и само утверждение является ложным. Другой способ — доказательство следствий отрицания тезиса, так как утверждение и его отрицание не могут быть одновременно истинными. Если верным является отрицание тезиса, то вопрос об истинности утверждения отпадает. Распространённым способом опровержения является опровержение фактами. Вполне достаточно, например, показать одного альбиноса, чтобы дать опровержение того, что альбиносы не существуют. Опровержение также используется в эвристике. В научной эвристике при выдвижении гипотезы или теории происходит последующая их проверка опытом. В случае, если они опровергаются эмпирическими данными, это показывает ограниченность их применения или ошибочность. Правила аргументации. АРГУМЕНТИРОВАНИЕ — это сугубо логический процесс, суть которого в том, что в нем обосновывается истинность нашего суждения (т. е. аргументов или, как их проще называют, доводов). Аргументация достигает цели, когда соблюдаются правила доказательства. Начнем с правил формулирования предмета нашего доказательства, т. е. с ПРАВИЛ ПОСТРОЕНИЯ ТЕЗИСА. 1. ТЕЗИС доказательства нужно СФОРМУЛИРОВАТЬ ЯСНО И ЧЁТКО. При этом нельзя допускать двусмысленности (Например, формулировка тезиса «законы надо выполнять» — двусмысленна, ибо неясно, о каких законах идет речь: о законах природы или о законах общественной жизни, которые не зависят от воли людей, либо о законах юридических, которые зависят только от воли граждан). Это требование очень важно, ибо любая ошибка в выборе слова, возможность двоякого истолкования фразы, нечеткая форма изложения мысли — все это может быть истолковано против вас, когда вы хотите что-либо доказать. 2.В ходе доказательства ТЕЗИС ДОЛЖЕН ОСТАВАТЬСЯ НЕИЗМЕННЫМ, т. е. должно доказываться одно и то же положение. В противном случае вы не сможете доказать свою мысль. Значит, в течение всего доказательства нельзя отступать от первоначальной формулировки тезиса. Поэтому на протяжении всего доказательства вам вашу формулировку тезиса надо держать под контролем.
Доказательство и опровержение, аргументация и критик» чаще всего проводятся в процессе спора. Различают следующиг виды споров по их цели: 1) научная дискуссия (цель — решение научной проблемы);
Гипотеза – это научно обоснованное предположение о причинах или взаимосвязях каких-либо явлений или событий природы, общества и мышления.
Как правило, термин «теория» употребляется в двух смыслах: широком и узком.
СОФИЗМЫ КАК ЭЛЕМЕНТ СПОРА Софизм – это преднамеренное, но тщательно замаскированное нарушение требований логики. Его целью является выдача лжи за истину. Как преднамеренной ошибке ему противостоит паралогизм – непроизвольная логическая ошибка.
Закон противоречия. Закон противоречия является фундаментальным логическим законом, на котором построена вся современная математика. Он является тавтологией классической логики, а также большинства неклассических логик, в том числе интуиционистской логики. Все же, существуют нетривиальные логические системы, в которых он не соблюдается, например логика Клини. Закон непротиворечия. Закон непротиворечия (закон противоречия) — закон логики, который гласит, что два несовместимых (противоречащих либо противоположных) суждения не могут быть одновременно истинными. По крайней мере одно из них необходимо ложно. Вероятно, каждый в своей жизни сталкивался с ситуацией, когда предмет, о котором он брался рассказать, оказывался настолько трудным, что скоро нить рассуждений ускользала и в мыслях начиналась путаница. Это происходит из-за того, что предмет недостаточно известен рассказчику или он не осуществил необходимой подготовки. Как только теряется ясная «дорожка» рассуждения, начинаются противоречия. Рассуждающий может, зачастую сам того не замечая, высказывать противоречащие суждения одно следом за другим. Именно о недопустимости противоречия между сказанным ранее и сказанным вновь и говорит закон непротиворечия. Также противоречием является приписывание одному и тому же предмету свойств, ранее отвергнутых, и наоборот. Такое противоречие называют формально-логическим. Закон исключённого третьего Закон исключенного третьего связан с противоречащими суждениями. Он означает, что может быть лишь два противоречащих друг другу суждения, третьего быть не может. Отсюда и пошло название данного закона. Если два суждения отрицают друг друга, одно что-либо утверждает, а другое противоречит существованию утверждаемого, можно говорить о том, что эти суждения являются противоречащими. Каждое из этих суждений является самостоятельным и рассматривается отдельно в силу того, что содержит информацию, отрицающую противное суждение. Рассмотрение их в этом плане производится для того, чтобы определить, какое из них истинно, а какое – ложно. Поскольку такие суждения полностью исключают друг друга, т. е. при ис
|
||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 496; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |

 есть
есть 
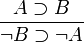 . То есть: посылка: если A, то B; заключение: следовательно, если не B, то не A.
. То есть: посылка: если A, то B; заключение: следовательно, если не B, то не A. . То есть: посылка: если A и B, то C; заключение: следовательно, если A и не C, то не B.
. То есть: посылка: если A и B, то C; заключение: следовательно, если A и не C, то не B. . То есть: первая посылка: если A, то B; вторая посылка: если B, то C; заключение: следовательно, если A, то C.
. То есть: первая посылка: если A, то B; вторая посылка: если B, то C; заключение: следовательно, если A, то C.
 (сложная)
(сложная)
 (сложная)
(сложная)


