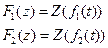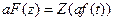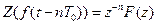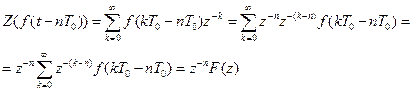Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Z-перетворення, функція переносу.Содержание книги
Поиск на нашем сайте
Одним із способі аналізу дискретних послідовностей є z-перетворення. Перетворення полягає у тому, що послідовності чисел {x(k)} ставиться у відповідність функція комплексної змінної z, яка визначається наступним чином:
Z-перетворення є більш узагальненим, ніж перетворення Лапласа і перетворення Фур’є: X(z) ---> X(p) ---> X(ω)
Z-перетворення є неоднозначним. До основних властивостей z-перетворення належать:
1. Лінійність. До z-перетворення застосовується принцип суперпозиції: Якщо {x1(k)} <---> X1(z) і {x2(k)} <---> X2(z), тоді {ax1(k) + bx2(k)} <---> aX1(z) + bX2(z).
2. Затримка. Якщо z-перетворення послідовності {x(k)} дорівнює X(z), то z-перетворення послідовності, затриманої на k0 тактів (y(k)=x(k-k0)), буде мати вигляд:
Таким чином, при затримці послідовності на k0 тактів необхідно помножити її z-перетворення на
3. Згортка. Згортка двох нескінченних послідовностей {x1(k)} і {x2(k)} визначається наступним чином:
Z-перетворення для послідовності {y(k)}:
Згортці двох дискретних послідовностей відповідає добуток їх z-перетворень. Зворотне z-перетворення:
Практичний розрахунок зворотного z-перетворювання виконується розкладанням Х(z) на прості дроби. Наприклад:
Отже:
Функція переносу. Функція переносу нерекурсивного фільтру.
Для нерекурсивного цифрового фільтра функція переносу визначається наступним чином:
Візьмемо z-перетворення:
Функція переносу для нерекурсивного фільтра дорівнює z-перетворенню від коефіцієнтів фільтра ак. Функція переносу рекурсивного фільтру.
Візьмемо z-перетворення:
=>
Функція переносу для рекурсивного фільтра дорівнює відношенню z-перетворення вихідної послідовності до z-перетворення вхідної послідовності відлікових значень, або відношення z-перетворення від коефіцієнтів ак до z-перетворення від коефіцієнтів bк. Основні теореми Z-перетворення.
1. Сумування та віднімання Z-пер.
2. Помноження на константу
3. Зсув на n-тактів по часовій області
- це тоді, коли f (t)=0, t <0
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.23.138 (0.006 с.) |

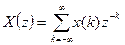 - симетричне;
- симетричне; - несиметричне;
- несиметричне;

 . Множник
. Множник 
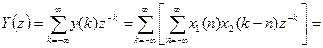
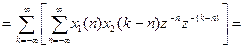

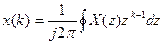


 . Функцією переносу G(z) називається відношення z-перетворення вихідної послідовності цифрового фільтра до z-перетворення вхідної послідовносты. Функція переносу є аналогом передаточної функції G(ω) і перетворюється у таку, якщо
. Функцією переносу G(z) називається відношення z-перетворення вихідної послідовності цифрового фільтра до z-перетворення вхідної послідовносты. Функція переносу є аналогом передаточної функції G(ω) і перетворюється у таку, якщо 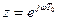 .
. - нерекурсивний фільтр.
- нерекурсивний фільтр.
 , де A(z) – z-пер. Від коефіцієнтів, X(z) – z-пер. від вхідної послідовності.
, де A(z) – z-пер. Від коефіцієнтів, X(z) – z-пер. від вхідної послідовності. - функція переносу для нерекурсивного фільтра.
- функція переносу для нерекурсивного фільтра. - рекурсивний фільтр.
- рекурсивний фільтр. , де bo*=1, b1*=-b1, bk*=-bk
, де bo*=1, b1*=-b1, bk*=-bk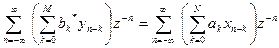 =>
=> 

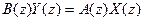
 - функція переносу для рекурсивного фільтра.
- функція переносу для рекурсивного фільтра.