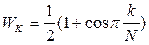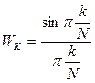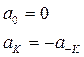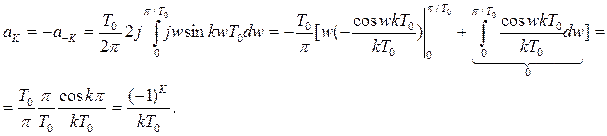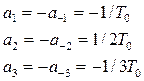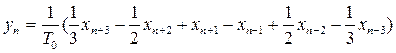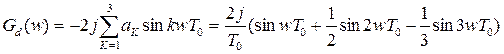Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особливості електронних систем.Содержание книги
Поиск на нашем сайте
ЗМІСТ
до Z-перетворення. 46
ДОДАТКОВІ ПИТАННЯ 5. Моделювання вузлів телевізійної системи багатовимірними фільтрами. 56 6. Апроксимуюча функція по частоті вимірювання для ланки кінескоп-зоровий аналізатор. 57 7. Апроксимуюча функція по площі для ланки кінескоп – зоровий аналізатор. 57 9. Математична модель ланки кінескоп – зоровий аналізатор. 57 24. Z-перетворення для експоненціальної функції. 58 28. Скласти структурну схему ЛЦФ yn=0.3xn+1,2xn+1-0,7yn-1 і розрахувати мпульсний відгук ЛЦФ. 59 Математичні моделі. Основним сучасним методом проектування та дослідження ЕС є метод математичного моделювання. Відмінною особливістю є: можливість прогнозування і оптимізації процесів, об’єктів і систем, натурний експеримент яких не можливий або при наявності утруднень. Обчислювальний експеримент скорочує кроки розробки, підвищує достовірність. Дослідження (теоретичне та експериментальне) проводиться над моделями. Однією із важливих задач є розробка моделей ЕС, адекватних з необхідною точністю до реальних об’єктів. Типи моделей: · Фізичні (макет) · Абстрактні (інформаційні, сенсуальні (чуттєві), концептуальні, математичні)
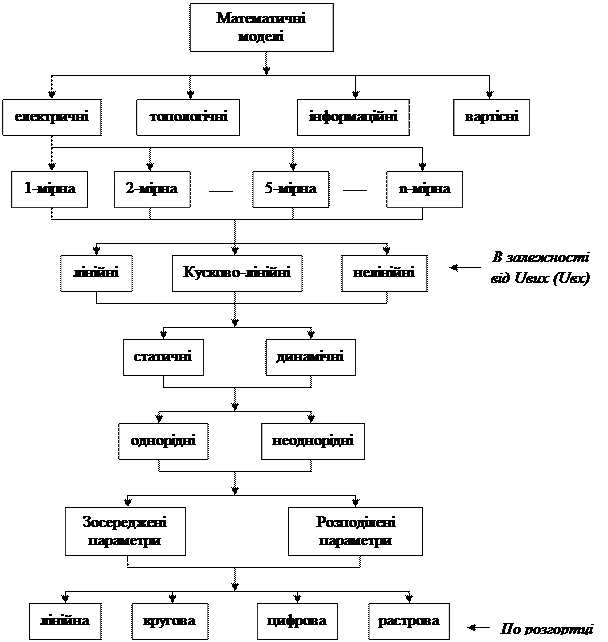
Математичні моделі
. В залежності від мірності кожна з моделей може бути одномірною, двомірною....n-мірною. В залежності від амплітудної характеристики – лінійні та нелінійні. В залежності від часу – статичні та динамічні.
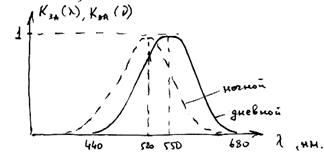
Энергетические диапазон воспринимаемых яркостей порог световой чувствительности абсолютный порог (достигается в ходе теневой адаптации) яркость адаптации 10-1000 кд/м2 рабочие яркости 50-180 кд/м2 слепящая яркость (225 000 Кд/м2) контрастность (диф. порог, то есть минимально различимая величина между двумя значениями яркости, воспринимаемыми как разные) прямой K=(Lфона-Lоб)/Lфона*100 % обратный K=(Lоб-Lфона)/Lоб*100 % относительная видность (чувствительность к лучам с разной длиной волны) Информационные пропускная способность на уровне ощущения (5,6*10^9 ед/сек) на уровне идентификации (20-70 ед/сек) на уровне восприятия (2-4 ед/сек) Пространственные острота зрения (зависит от овещённости, контрастности, времени экспозиции, положения поля зрения, формы) поля зрения зона центрального зрения (2°-4°) ясного зрения (30°-35°) переферийного (180°) объём восприятия (7±2) Временные латентный период реакции (от ощущения до идентификации ~200 мс) длительность инерции ощущения (меньше, если объект в зоне центр зрения) время зрительной фиксации (0,2-0,65 с, зависит от сложности фигуры) критическая частота мелькания (серия световых импульсов, воспринимаемая как непрерывный сигнал) f=a*logL+b (то есть зависит от яркости) ~14-70 Гц время адаптации темновая (~ 2-10 мин) световая (~ 0,1 — 0,8 мин) длительность инфопоиска (0,8 — 1,5 сек)
ЗА – зоровий аналізатор.
ЗА можна представити 5-ти мірним фільтром Ф1 – зоровий аналізатор Ф1 Ф2
Ф4 Ф5 Ф6 Ф7 Ф8
Якщо потужність випромінювання нормується до
АЧХ -
Можна замінити НЧ фільтром:
Апаратна функція:
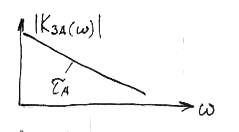
Характеристики фільтра зорового аналізатора:
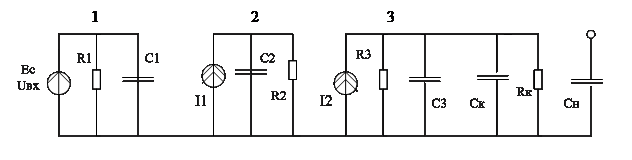
Схемна модель індикатора. Схема складається з макромоделі кінескопа і макромоделі підсилювача. Макромодель підсилювача (однокаскадний): 1 ланка: вхідна – моделює вхідний опір та ємність; 2 ланка: вихідна – враховує вихідний опір та ємність; 3 ланка: середня – моделює АЧХ і коеф. підсилення.
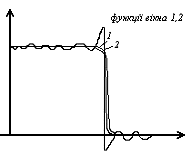
Функція вікна в ЛЦФ.
Із збільшенням порядку фільтру середньоквадратичне відхилення
При цьому спостерігається викид – явище Гіббса. А із збільшенням порядку фільтру цей викид збільшується.
Щоб убрати вплив викида, водять функцію вікна:
Функція вікна Ланчоса:
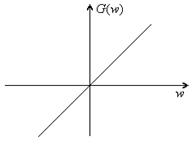
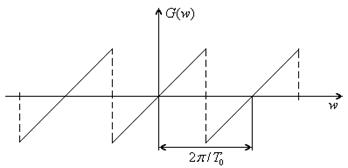
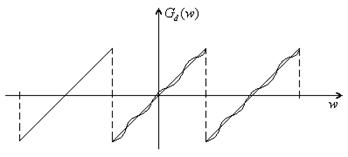
Диференцюючий ЛЦФ.
При N = 3:
Характеристику можна згладити, якщо використати згладжувальний коефіцієнт.
Етапи проектування ЕС. ЗМІСТ
до Z-перетворення. 46
ДОДАТКОВІ ПИТАННЯ 5. Моделювання вузлів телевізійної системи багатовимірними фільтрами. 56 6. Апроксимуюча функція по частоті вимірювання для ланки кінескоп-зоровий аналізатор. 57 7. Апроксимуюча функція по площі для ланки кінескоп – зоровий аналізатор. 57 9. Математична модель ланки кінескоп – зоровий аналізатор. 57 24. Z-перетворення для експоненціальної функції. 58 28. Скласти структурну схему ЛЦФ yn=0.3xn+1,2xn+1-0,7yn-1 і розрахувати мпульсний відгук ЛЦФ. 59 Особливості електронних систем. Електронна система (ЕС) – це складна єдина структура, побудована на взаємодіючих між собою автономних складових частинах, що вирішують спільне завдання, взаємозв’язані по єдиному правилу, підкорені єдиному алгоритму. Особливість. У електронних приладах фізичні процеси можуть фундаментально відрізняються =, але системне функція, яку вони виконують при об’єднанні може залишатися незмінно, алгоритм роботи системи зберігається, або докорінно не змінюється. Електронна система складається із менш складних підсистем, кожну з яких можливо поділити на менш складні частини і продовжувати ділення системи до елементів. Дана електронна система називається відкритой, якщо в процесі її функціонування можуть відключатися її окремі елементи та приєднуватися нові без порушення системних якостей. Особливості ЕС. В основі вибору структури полягає ряд відмітних ознак 1. Принцип замкненості життєвого циклу ЕС. Полягає в реалізації етапів її створення та застосування. 2. Принцип цілеспрямованості системи. Кожна система слугує для виконання певної мети. 3. Принцип цілісності. При об’єднанні елементів системи, виникають нові властивості. 4. Принцип вкладеності. Менша вкладається в більшу. 5. Принцип лінійності. Система називається лінійною, якщо її коефіцієнт передачі лінійний. Коли система лінійна, для неї діє принцип суперпозиції – комбінація вхідних возмущений викликає лінійну комбінацію вихідних возмущений. 6. Принцип стаціонарності. Стаціонарна ЕС – при будь-якому зсуву у часі вхідного возмущения без змінення форми, реакція зазнає такого же зсуву у часі. У нестаціонарній ЕС при зсуві вихідного возмущения без змінення форми їх вихідні дані не тільки зсуваються у часі, але й змінює форму.
Математичні моделі. Основним сучасним методом проектування та дослідження ЕС є метод математичного моделювання. Відмінною особливістю є: можливість прогнозування і оптимізації процесів, об’єктів і систем, натурний експеримент яких не можливий або при наявності утруднень. Обчислювальний експеримент скорочує кроки розробки, підвищує достовірність. Дослідження (теоретичне та експериментальне) проводиться над моделями. Однією із важливих задач є розробка моделей ЕС, адекватних з необхідною точністю до реальних об’єктів. Типи моделей: · Фізичні (макет) · Абстрактні (інформаційні, сенсуальні (чуттєві), концептуальні, математичні)
Математичні моделі
. В залежності від мірності кожна з моделей може бути одномірною, двомірною....n-мірною. В залежності від амплітудної характеристики – лінійні та нелінійні. В залежності від часу – статичні та динамічні.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.51.237 (0.014 с.) |

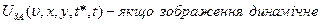
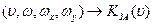
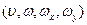
 Ф3
Ф3 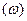
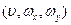
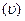
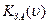 , то ми маємо оптичні характеристики.
, то ми маємо оптичні характеристики.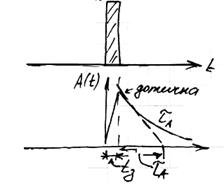
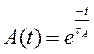
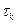 -залежність від освітленості 10-200кд/м*м,
-залежність від освітленості 10-200кд/м*м, 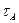 =0.06с
=0.06с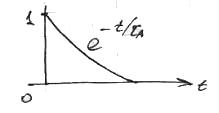
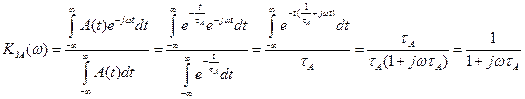
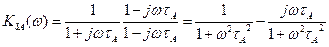
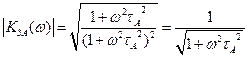
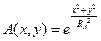 - імпульсна характеристика за по відношенню до x,y.
- імпульсна характеристика за по відношенню до x,y.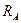 - ефективний радіус зорового аналізатора
- ефективний радіус зорового аналізатора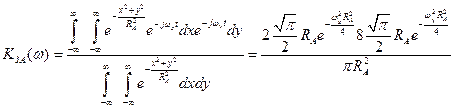
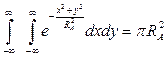
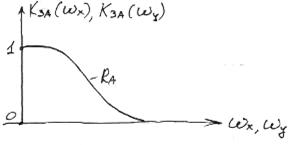
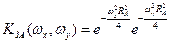 - частотна характеристика ЗА
- частотна характеристика ЗА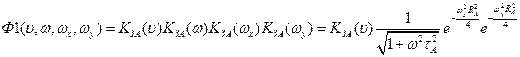
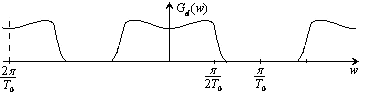
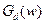 від прямокутної характеристики буде зменшуватись.
від прямокутної характеристики буде зменшуватись.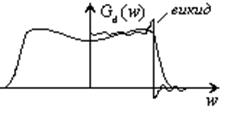
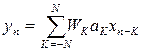 .
.