
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Утверждено Учебно-методическим Советом ЧГИФК,Содержание книги
Поиск на нашем сайте
Воеводина Г.Н. Методические указания по изучению курса «Математика» студентам, занимающимся По индивидуальному Графику Методические указания
Чайковский, 2004 ББК 22.1 В 63 Воеводина Г.Н. Методические указания по изучению курса «Математика» студентам, занимающимся по индивидуальному: Методические указания. Чайковский: ЧГИФК, 2004. – 23 с.
Утверждено Учебно-методическим Советом ЧГИФК, Протокол № 10 от 28.06.06. Методические указания предназначены для оказания помощи студентам, занимающимся по индивидуальным графикам, в организации их самостоятельной работы по овладению системой знаний и навыков в объеме действующей программы с целью подготовки к экзамену. Рецензент: д.т.н. профессорГерасимов Е.Н. © Чайковский государственный институт физической культуры © Воеводина Г.Н. Содержание Введение 4
Учебно-тематический план 5
Программа курса 6
Планы практических занятий 8
Контрольные задания для самостоятельной работы 17
Вопросы для подготовки к экзамену 20
Список литературы 22 Введение Программа курса «Математика» разработана в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования для обучения студентов по специальности 022300 «Физическая культура и спорт». Курс рассчитан на 140 часов занятий, из которых 30 часов – лекции, 40 часов – практические занятия и 70 часов самостоятельные занятия. Учебно-тематический план курса «Математика»
Программа курса «Математика» Тема 1. Аналитическая геометрия Вектор, действия над векторами. Прямоугольный базис. Разложение вектора по базису, длина вектора, проекция вектора. Скалярное и векторное произведение.
Расстояние между двумя точками. Деление отрезка в данном отношении. Площадь треугольника. Уравнение прямой, с угловым коэффициентом, уравнение прямой в отрезках. Уравнение прямой, проходящей через две данные точки. Общее уравнение прямой. Уравнение прямой в отрезках. Уравнение прямой, проходящей через данную точку в данном направлении. Угол между прямыми. Взаимное расположение прямых. Нормальное уравнение прямой. Уравнение окружности, эллипса, гиперболы и параболы. Тема 2. Алгебра матриц Определение и виды матриц. Операции над матрицами. Определители, свойства определителей. Минор. Алгебраическое дополнение, разложение определителя по строке или столбцу. Ранг матрицы.
Тема 3. Система линейных алгебраических уравнений Система линейных алгебраических уравнений. Условие Кронекера-Капелли совместимости системы. Решение системы линейных уравнений методом Гаусса, методом Крамера.
Тема 4. Основы дифференциального исчисления Числовые последовательности и функции, способы их задания и свойства. Сложные и обратные функции, их графики. Класс элементарных функций. Предел числовой последовательности. Предел функции в точке. Свойства пределов, бесконечно малые и бесконечно большие величины, их сравнение. Замечательные пределы. Непрерывность функции. Свойства функций непрерывных на отрезке. Производная функции. Необходимое условие существования. Правила дифференцирования. Производная сложной и обратной функции. Производные элементарных функций. Производные высших порядков. Теорема Ферма и Лагранжа. Правило Лопиталя. Точки экстремума и перегиба функции. Асимптоты функций. Общая схема исследования функции. Дифференциал функции. Уравнение касательной и нормали к графику функции. Тема 6. Ряды Числовые ряды. Основные понятия. Свойства сходящихся рядов. Необходимый признак сходимости. Гармонический ряд. Знакопостоянные ряды. Признаки сходимости. Знакочередующиеся ряды. Признак сходимости Лейбница. И математической статистики Основные понятия теории вероятностей. Пространство элементарных событий. Основные формулы для вычисления вероятностей. Основные понятия комбинаторики. Независимые и зависимые события. Условная вероятность. Формула полной вероятности. Теорема Байеса. Формула Бернулли. Определение случайной величины. Дискретные и непрерывные случайные величины. Закон распределения дискретной случайной величины. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение. Функция распределения непрерывной случайной величины.
Планы практических занятий Тема 3. Алгебра матриц 1. Повторение определений основных понятий темы. 2. Даны матрицы А и В
Указать, какие из нижеприведенных операций выполнимы и выполнить их. а) А+B б) АТ+B; в) А+BТ; г) АТ +BТ д) 3А - 3.Найти определители матриц
Тема 5. Предел функции 1. Повторение определений основных понятий темы. 2. Вычислить пределы: а) в) д
3. Правило Лопиталя раскрытия неопределенностей 4. Вычислить предел по правилу Лопиталя
Тема 10. Ряды. 1. Повторение определений основных понятий темы. 2. Записать формулу общего члена ряда: а) 3. Найти сумму ряда, доказав, что он сходится а) 4. Исследовать сходимость числового ряда:
5. Исследовать сходимость знакопеременного числового ряда:
Тема 12. Комбинаторика 1. Повторение определений и формул основных понятий темы: 2. Вычислить значения следующих выражений а) 3. Сократить дроби: а) 4. Решить уравнения: а) в) 5. Решить задачи: а) Из цифр 1,2,3,4, составлены всевозможные двузначные числа, так чтобы в каждом числе не было одинаковых цифр. Сколько чисел можно составить? б) Сколькими способами можно выбрать четырех человек на четыре различные должности из 9 кандидатов? в) Энциклопедия состоит из 8 томов. Сколькими способами её можно поставить на полке в произвольном порядке? Случайной величины. 1. Повторение определений основных понятий темы. 2. Стрелок, имея 4 патрона стреляет до первого попадания в цель. Вероятность попадания при каждом выстреле равна 0,6. Построить закон распределения числа использованных патронов. 3. Урна содержит 5 черных и 10 красных мячей. Вынимаются наудачу два мяча. Составьте закон распределения числа извлеченных черных мячей. 4. Куплено 500 лотерейных билетов, причем на каждый из 40 билетов выпал выигрыш в 10 рублей, 10 билетов принесли их владельцам выигрыш по 50 рублей, 5 билетов - по 100 рублей. Найдите средний выигрыш, выпавший на один билет. 5. Случайная величина X принимает значение 7, -2,1,-5,3 с равными вероятностями. Найдите МХ. 6. Случайная величина Х имеет закон распределения
Найдите D (3Х-2): 1) предварительно составив закон распределения случайных величин 3Х – 2; 2) Используя свойства дисперсии. 7. Случайная величина Х – число очков, выпавших при однократном бросании игральной кости. Определить Контрольные задания для самостоятельной работы Прямая на плоскости 1. Докажите, что прямая, на которой лежат точки А (-3;2) и В(9;-6), проходит через начало координат. Сделайте чертёж. 2. Отрезок, ограниченный точками С (-8;9) и К (-2;3), разделён на четыре части. Вычислите координаты точек деления. 3. Вычислите периметр треугольника с вершинами А (3;4), В (3;8), 4. Составьте уравнение прямой, проходящей через т.А (2;-3) параллельно прямой x+9y-11=0.
5. Две прямые пересекаются в т. С (-2;- 4). Найти угол между ними, если одна из них проходит через точку А (1;2), а другая – через т. В (1;-3). Сделайте чертёж. 6. Установить пересекаются ли в одной точке три прямые 2х+3y-1=0; 4х-5y+5=0; 3x-y+2=0. 7. Треугольник задан вершинами А (-6;-2), В (4;8) и С (2;-8). Найти: 1. уравнение медианы СD; 2. уравнение высоты АЕ.
Кривые второго порядка 1. Составить уравнение радиуса окружности х2 + у2 + 4х + 2у – 32 = 0, проведённого в точку на ней А (4;-2). 2. Составить уравнение эллипса с фокусами на оси Ох, если расстояние между его фокусами равно 16, а эксцентриситет равен ½. 3. Найти эксцентриситет гиперболы
4. Составить уравнение оси параболы у2 - 6у - 12у - 15 = 0. 5. Составить уравнение директрисы параболы х2 - 4х - 16у - 52 = 0. Итоговая контрольная работа Вариант 1. 1. Вычислить площадь фигуры, ограниченной линиями: 2. Найти решения дифференциальных уравнений: а) (1+х)уdх – (1+у)хdy = 0 б) у’- 2у-7 = 0, если у = -1; х = 0. 3. Бригадир должен отправить на работу бригаду из 3 человек. Сколько таких бригад можно составить из 8 человек. 4. Случайные величины Х и У независимы и имеют соответственно законы распределения
Найти Д (2Х+3У) Вопросы для подготовки к экзамену 1. Векторы. Действия над векторами. 2. Разложение вектора по базису. Длина вектора. Проекция вектора. 3. Скалярное произведение двух векторов и его основные свойства. 4. Векторное произведение векторов и его основные свойства. 5. Расстояние между двумя точками. Деление отрезка в данном отношении. 6. Уравнение прямой с угловым коэффициентом. 7. Уравнение прямой проходящей через две данные точки. 8. Уравнение прямой в отрезках. 9. Общие уравнения прямой. 10. Уравнение прямой, проходящий через данную точку в данном направлении. 11. Угол между прямыми. 12. Взаимное расположение прямых. 13. Нормальное уравнение прямой. 14. Уравнение окружности эллипса, гиперболы, параболы. 15. Матрицы. Действия над матрицами. 16. Определители. Свойства определителей. 17. Решение систем линейных уравнений методом Гаусса. 18. Решение систем линейных уравнений методом Крамера. 19. Теорема Кронекера-Капелли о совместности систем. 20. Функции. Способы задания и свойства функции. 21. Предел числовой последовательности. Основные свойства. 22. Предел функции. Основные теоремы о пределах. 23. Первый и второй замечательные пределы. 24. Непрерывность функции. Точки разрыва. Свойства функций непрерывных на отрезке.
25. Определение производной. Геометрический и физический смысл производной. 26. Производные элементарных функций (ех,lnx? ax, xn; sin x; cos x; tg x; arcsin x; arctgx). 27. Правила дифференцирования сложной функции. 28. Правило Лопиталя 29. Возрастание и убывание функции. Экстремумы. 30. Исследование функции на выпуклость. Точки перегиба. 31. Асимптоты. 32. Исследование функции и построения графиков функций. 33. Неопределенный интеграл и его свойства. 34. Методы интегрирования. 35. Определенный интеграл и его свойства. 36. Геометрический смысл определенного интеграла. 37. Несобственные интегралы и их сходимость. 38. Числовые ряды. Признаки сходимости. 39. Основные понятия о дифференциальных уравнениях. 40. Дифференциальные уравнения с разделяющимися переменными. 41. Однородные дифференциальные уравнения. 42. Линейные дифференциальные уравнения первого порядка. 43. Основные формулы для вычисления комбинаторики. 44. Основные формулы для вычисления вероятностей. 45. Независимые и зависимые события. Условная вероятность. 46. Формула полной вероятности. 47. Формула Бернулли. 48. Определение случайной величины. Дискретные и непрерывные случайные величины. 49. Законы распределения дискретной случайной величины. 50. Математическое ожидание, дисперсия, среднее квадратическое отклонение дискретной случайной величины. 51. Функция распределения непрерывной случайной величины. 52. Математическое ожидание и дисперсия непрерывной случайной величины.
Список литературы Основная литература. 1. Баврин И.И., Матросов В.Л. Общий курс высшей математики. М.: Просвещение, 1998. 2. Гресс П.В. Математика для гуманитариев. М.: Юрайт, 2000. 3. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. Часть I и II. М.: Высшая школа, 1999. 4. Кремер Н.Ш. Высшая математика для экономистов. ЮНИТИ, 1997. 5. Шипачев В.С. Математический анализ. М.: Высшая школа, 1999.
Дополнительная литература. 1. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1977. 2. Бернант А.Ф. Краткий курс математического анализа для ВТУЗОВ. М.: Наука, 1973. 3. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗОВ. М.: Наука,1964. 4. Бугров Я.С., Никольский С.М. Сборник задач по высшей математике. М.: Высшая школа, 1997. 5. Головина Л.И. Линейная алгебра и некоторые ее приложения. М.: Наука, 1975. 6. Ефимов А.В., Демидович Б.Г. Сборник задач по математике. М.: Наука, 1986. 7. Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике. М.: Высшая школа, 1991. 8. Никольский С.М. Элементы математического анализа. М.: Наука, 1981. 9. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т. I и II. М.: Наука, 1976. 10. Ефимов Н.В. «Краткий курс аналитической геометрии» М. 1962 г 11. Гурский Е.И. Теория вероятностей с элементами математической статистики. М. Высшая школа 1971г. 12. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М. Наука. 1970г. Воеводина Г.Н. Методические указания по изучению курса «Математика» студентам, занимающимся по индивидуальному графику Методические рекомендации
Изд. лиц. № 00539от 06.12.1999 Тираж 100 экз. Заказ №160 Ауд. 229-230
Воеводина Г.Н. Методические указания по изучению курса «Математика» студентам, занимающимся По индивидуальному Графику Методические указания
Чайковский, 2004 ББК 22.1 В 63 Воеводина Г.Н. Методические указания по изучению курса «Математика» студентам, занимающимся по индивидуальному: Методические указания. Чайковский: ЧГИФК, 2004. – 23 с.
Утверждено Учебно-методическим Советом ЧГИФК, Протокол № 10 от 28.06.06. Методические указания предназначены для оказания помощи студентам, занимающимся по индивидуальным графикам, в организации их самостоятельной работы по овладению системой знаний и навыков в объеме действующей программы с целью подготовки к экзамену. Рецензент: д.т.н. профессорГерасимов Е.Н. © Чайковский государственный институт физической культуры © Воеводина Г.Н. Содержание Введение 4
Учебно-тематический план 5
Программа курса 6
Планы практических занятий 8
Контрольные задания для самостоятельной работы 17
Вопросы для подготовки к экзамену 20
Список литературы 22 Введение Программа курса «Математика» разработана в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования для обучения студентов по специальности 022300 «Физическая культура и спорт». Курс рассчитан на 140 часов занятий, из которых 30 часов – лекции, 40 часов – практические занятия и 70 часов самостоятельные занятия. Учебно-тематический план курса «Математика»
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.249.160 (0.022 с.) |



 ; е) А.B; ж) АТ.B; з) B. АТ
; е) А.B; ж) АТ.B; з) B. АТ
 ; б)
; б) 

 ;
;  ;
; ;
;  ;
;
 ; б)
; б) 
 ; г)
; г) 
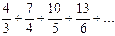 ; б)
; б) 

 ;
;  ;
; ;
;  ;
; ;
;  ;
; 
 ;
;  ;
; 
 ; б)
; б)  ; в)
; в) 
 ; б)
; б)  ; в)
; в) 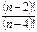 .
. ; б) 6Рх=Рх+2
; б) 6Рх=Рх+2 ; г)
; г) 
 .
.



