Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В результате получаем общее решение системыСодержание книги Поиск на нашем сайте
Одно базисное решение получаем при x4=x5=0, т.е. x1=3,5; x2=0,5; x3=3 или X1=(3,5; 0,5; 3; 0; 0). Чтобы получить другое базисное решение, достаточно задать x4=1; x5=0, тогда x1=6; x2=1; x3=2 или X2=(6; 1; 2; 1; 0). Пример 7. Найти характеристические числа и собственные векторы линейного преобразования с матрицей А = Решение: Запишем линейное преобразование в виде: Составим характеристическое уравнение:
l2 - 8l + 7 = 0; Корни характеристического уравнения: l1 = 7; l2 = 1; Для корня l1 = 7: Из системы получается зависимость: x1 – 2x2 = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (t; 0,5t) где t - параметр.
Для корня l2 = 1: Из системы получается зависимость: x1 + x2 = 0. Собственные векторы для второго корня характеристического уравнения имеют координаты: (t; -t) где t - параметр.
Полученные собственные векторы можно записать в виде:
Пример 8. Дано комплексное число z. Требуется: 1. записать число z в алгебраической и тригонометрической формах; 2. найти все корни уравнения
Решение: 1) Комплексное число z в алгебраической форме имеет вид: z=а+bi; в тригонометрической форме: z=r(cosj+i×sinj), где Для тог чтобы записать
2) Так как число
Применяя формулу для извлечения корня из комплексного числа:
получаем Если k=0, то Если k=1, то Если k=2, то Следовательно, корни уравнения в алгебраической форме имеет вид Ответ:
Пример 9. Даны два линейных преобразования:
Средствами матричного исчисления найти преобразование, выражающее x1¢¢, x2¢¢, x3¢¢ через x1, x2, x3. Решение: Первое преобразование определяется матрицей A, а второе ¾ матрицей B, где
Искомое преобразование является произведением данных преобразований с матрицей
Перемножив матрицы B и A, получим матрицу
Следовательно, искомое преобразование таково:
Пример 10. Вычислить пределы функций, не пользуясь правилом Лопиталя: а) Функция
б) Ни числитель, ни знаменатель этой дроби не имеют конечного предела так как они неограниченно возрастают при неограниченном возрастании х, т. е. имеем дело с неопределенностью
так как в) Поскольку числитель и знаменатель обращаются в нуль при х=0, то имеем дело с неопределенностью вида Воспользуемся тригонометрической формулой для преобразования знаменателя 2sin2x=1-cos2x и получим предел, в котором участвует тригонометрическая функция sinx. Применив первый замечательный предел
так как г) Предел функции Преобразуем выражение в скобках к виду
Тогда
т. к.
Пример 11. Задана функция y=f (x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
Решение: Область определения функции – вся числовая ось (-¥;+¥). В интервале (-¥;0] функция непрерывна, так как это линейная функция f (x)=- х. В интервале (0;2] эта функция непрерывна, так как это степенная функция f (x)=- х2 и ее графиком является парабола. В интервале (2;+¥) функция непрерывна, так как это линейная функция f (x)= х+1. Внимание надо обратить на точки х=0 и х=2, так называемые точки стыка. Найдем предел f (x) в точке х=0 слева и справа и сравним их. Слева от точки х=0 функция задана формулой f (x) =-х, а справа - f (x) =-х2, тогда
Так как 2. Аналогично исследуем на непрерывность функцию в точке x=2.
Так как эти пределы различны Построим график.
Пример 12. а) Найти производную функции Решение: Сначала преобразуем данную функцию:
б) Найти производную функции Решение:
в) Найти производную функции Решение:
г) Найти производную функции Решение: Логарифмируем данную функцию
Дифференцируем
Выражаем
Или
д) Найти производную Решение: Функция задана неявно, тогда дифференцируя, получаем:
Группируя слагаемые с
Окончательно получаем:
Пример 13. Исследовать функцию Решение. 1. Данная функция не определена при
2. 3. Не периодична. 4. Точки пересечения с осью Ох:
5. Исследуем на непрерывность. Точкой разрыва является
Значит, 6. Из предыдущего пункта следует, что Найдем наклонную асимптоту
Итак, 7. Исследуем на возрастание, убывание и экстремум функции. Для этого найдем производную функции.
Найдем точки, в которых производная равна нулю
Далее отметим данные точки на числовой оси и к ним добавляем точку
Находим интервалы, на которых
При прохождении точки
При прохождении точки
8. Исследуем на вогнутость функции и точки перегиба. Для этого находим производную второго порядка.
Вторая производная в ноль никогда не обращается, поэтому на числовой оси отмечаем только
Составим таблицу, в которую занесем полученные сведения.
После того, как собрали все данные, полученные в ходе исследования, изобразим характерное поведение графика данной функции. (См. рис.).
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.216.107 (0.009 с.) |

 .
. .
.




 .
. .
. и
и  .
. .
. - алгебраическая форма.
- алгебраическая форма. ,
,  ,
,  ,
, .
. - тригонометрическая форма.
- тригонометрическая форма. Þ
Þ  .
. в тригонометрической форме
в тригонометрической форме .
. ,
,
 ;
; ;
; .
. ,
, ,
, .
.





 ;
;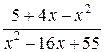 не определена при х=5 и поэтому разрывна в этой точке. Числитель и знаменатель в точке х=5 обращается в нуль, налицо неопределенность
не определена при х=5 и поэтому разрывна в этой точке. Числитель и знаменатель в точке х=5 обращается в нуль, налицо неопределенность  . Выделим общий множитель (х-5) и сократим на него числитель и знаменатель, считая х ¹ 5, х ® 5.
. Выделим общий множитель (х-5) и сократим на него числитель и знаменатель, считая х ¹ 5, х ® 5. .
. ;
; . Поделим числитель и знаменатель дроби на х2:
. Поделим числитель и знаменатель дроби на х2:
 ,
,  ,
,  ,
,  при х ® ¥ – величины бесконечно малые.
при х ® ¥ – величины бесконечно малые. ;
; , получаем:
, получаем: ,
, при х ® 0.
при х ® 0. .
. при х ® 0 равен единице, т.е. в данном примере требуется раскрыть неопределенность
при х ® 0 равен единице, т.е. в данном примере требуется раскрыть неопределенность  . Примеры такого вида сводятся ко второму замечательному пределу
. Примеры такого вида сводятся ко второму замечательному пределу  .
.
 .
. ,
, ,
,  .
.

 , то точка x=0 является точкой непрерывности функции.
, то точка x=0 является точкой непрерывности функции.

 , функция в точке x=2 терпит разрыв первого рода.
, функция в точке x=2 терпит разрыв первого рода.
 .
.

 .
.
 .
.
 .
. ,
, ,
, ,
, ,
, .
. .
.

 , получаем:
, получаем:
 .
. и построить график.
и построить график.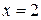 , т. к. в этой точке знаменатель обращается в ноль. Значит
, т. к. в этой точке знаменатель обращается в ноль. Значит .
.

 ,
,  . Следовательно, функция общего вида.
. Следовательно, функция общего вида. при
при  ,
,  . С осью Оу:
. С осью Оу:  ,
, . Нашли две точки пересечения графика функции с осями координат:
. Нашли две точки пересечения графика функции с осями координат:  и
и  .
. и
и  .
. .
. .
.  .
. - наклонная асимптота.
- наклонная асимптота. .
. .
.
 и
и  не определена.
не определена.

 :
:  и
и :
:  .
.
 .
. производная меняет знак с минуса на плюс. Следовательно,
производная меняет знак с минуса на плюс. Следовательно, 
 .
. .
.
 :
:  - функция вогнута и
- функция вогнута и  :
:  - выпукла. Точек перегиба нет.
- выпукла. Точек перегиба нет.