
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследовать функции методом дифференциального исчисления и схематично построить их графики.Содержание книги
Поиск на нашем сайте
121. а) 122. а) 123. а) 124. а) 125. а) 126. а) 127. а) 128. а) 129. а) 130. а)
Решение типового варианта Пример 1. Даны векторы Решение: Для того, чтобы три вектора могли образовывать базис пространства Вычислим определитель D системы.
Вывод: векторы Разложение вектора
где х1, х2, х3 – искомые координаты вектора В координатной форме это разложение имеет вид: (24;20;6)= х1 (2;4;1)+ х2 (1;3;6)+ х3 (5;3;1) или (24;20;6)=(2 х1 + х2 +5 х3;4 х1 +3 х2 +3 х3; х1 +6 х2 + х3). В левой и правой частях полученного равенства стоят два вектора. Они равны и поэтому равны их одноименные координаты. Получим систему трех уравнений с тремя неизвестными:
Систему решаем по формулам Крамера. Для этого, кроме определителя D, вычисляем D 1, D 1, D 3, полученные из определителя D заменой соответствующих столбцов столбцом свободных членов системы.
Координаты вектора
Таким образом, разложение вектора Проверка. Подставим в правую часть полученного разложения координаты векторов
Получили координаты вектора
Пример 2. Даны координаты вершин пирамиды ABCD: A(10; 6; 6), B(- 2; 8; 2), C(6; 8; 9), D(7; 10; 3). Найти: 1) Длину ребра АВ; 2) Угол между ребрами АВ и АD; 3) Уравнение прямой АВ; 4) Уравнение плоскости АВС; 5) Угол между ребром АD и гранью АВС; 6) Площадь грани АВС; 7) Объем пирамиды; 8) Уравнение высоты, опущенной из вершины D на грань АВС. Сделать чертеж. Решение: 1) Если ребро АВ обозначить за вектор
Если Следовательно,
2) Угол между ребрами АВ и АD – это угол между векторами
Из пункта 1) нам известны координаты вектора
Если векторы
Следовательно, получаем
Итак, 3) Уравнение прямой, проходящей через две точки М1(х1; у1; z1) и М2(х2; у2; z2) имеет вид:
или равносильное ему уравнение:
где Направляющий вектор прямой – это вектор, параллельный прямой. В нашем случае прямая проходит через точки А(10; 6; 6) и В(- 2; 8; 2).Следовательно, уравнение прямой АВ:
Итак, каноническое уравнение прямой АВ:
где направляющий вектор
4) Уравнение плоскости по трем точкам находится по формуле:
где А(х1; у1; z1); В (х2; у2; z2); С(х3; у3; z3) – точки, через которые проходит плоскость. Подставляя координаты точек А, В, С в формулу (*), получим:
Считаем определитель, разложив его по первой строке. D=а11А11+а12А12+а13А13, где
Итак, уравнение плоскости АВС:
5) Требуется найти угол между ребром АD и гранью АВС. Это равносильно нахождению угла между прямой АD и плоскостью АВС. Угол между прямой
где
Находим уравнение прямой АD по двум точкам:
Следовательно, АD: Т.к. уравнение плоскости АВС: Значит,
6) Площадь грани АВС – это площадь треугольника АВС. Если треугольник построен на векторах
Из пункта 1) имеем
Далее необходимо найти векторное произведение
находим длину полученного вектора:
Следовательно,
7) Объем пирамиды равен
Следовательно, 8) Грань АВС имеет нормальный вектор
Итак, получили уравнение высоты DH:
Пример 3. Даны вершины треугольника А(1;-1), В(-2;-6), С(-6;3). Требуется: 1) вычислить длину высоты и медианы, проведенной из вершины В; написать их уравнения; 2) написать уравнения прямой, проходящей через вершину В параллельно стороне АС; 3) найти угол между прямыми АВ и АС; 4) найти точку В1 симметричную точке В относительно прямой АС. Решение: 1.а) Составим уравнение медианы, проведенной из вершины В. Пусть М – середина АС. Найдем её координаты:
Уравнение прямой по двум точкам находится по формуле:
BМ: Приведем это уравнение к общему виду прямой. -14(х +2) = у +6 Þ -1 4х - 28 = у +6Þ ВМ: 14х+у+34=0. (Общий вид прямой А х + В у+С=0). Длину медианы ВМ вычисляем по формуле: Тогда 1.б) Составим уравнение стороны АС – основания высоты ВН по известным двум точкам АС: Приведем это уравнение к общему виду прямой. 4(х -1) = -7(у +1) Þ 4х - 4 = -7 у -7Þ АС: 4х+7у+3=0. Угловой коэффициент этой прямой Составим уравнение высоты ВН, зная, ее угловой коэффициент и точку В.
ВН: 7х-4у-10=0.
Вычислим длину высоты ВН, как расстояние от точки В до прямой АС, по формуле
2) Известно, что если прямые параллельны, то их угловые коэффициенты совпадают. Следовательно, т. к BL|| AC,то Составляем уравнение прямой BL, зная ее угловой коэффициент
3) Найдем угол между прямыми АВ и АС. Составим уравнение прямой АВ по известным двум точкам
Угловой коэффициент АВ: Воспользуемся формулой
Для данного случая
4) Из п.1.б) известны уравнения стороны АС: 4х+7у+3=0 и высоты ВН: 7х-4у-10=0. Найдем точку их пересечения:
выведем формулы Для данного случая получаем: Пример 4. Линия, заданная уравнением r=r(j) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от j=0 до j=2p и придавая j значения через промежуток 2) найти уравнение данной линии в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия:
Решение: 1) Рассмотрим первый способ построения кривой. Придавая углу значения через промежуток
По найденным точкам строим кривую в полярной системе координат (см. рис.)
Рис.
2) Перейдем к прямоугольным координатам, используя формулы:
Подставляя выражение для r и соsj в заданное уравнение
получаем:
Выполняем преобразования, чтобы освободиться от знаменателя.
Перенося 2х в правую часть и возводя в квадрат обе части равенства, имеем:
Преобразуя, получаем уравнение кривой в каноническом виде.
3) Полученное уравнение определяет параболу, ось симметрии которой ось абсцисс, а вершина находится в точке Данные результаты соответствуют результатам, полученным ранее (см. рис.).
Пример 5. Дана система линейных уравнений:
доказать ее совместность и решить тремя способами: 1) Методом Гаусса; 2) По формулам Крамера; 3) Средствами матричного исчисления. Решение: Теорема Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу ее расширенной матрицы, т. е. r (A) =r (A1), где
Расширенная матрица системы имеет вид:
Умножим первую строку на (–3),а вторую на (2); прибавим после этого элементы первой строки к соответствующим элементам второй строки; вычтем из второй строки третью. В полученной матрице первую строку оставляем без изменений.
Разделим элементы третьей строки на (6) и поменяем местами вторую и третью строки: ~ Умножим вторую строку на (–11) и прибавим к соответствующим элементам третьей строки. ~ Разделим элементы третьей строки на (10).
Найдем определитель матрицы А.
Следовательно, r (A) =3. Ранг расширенной матрицы r (A1) так же равен 3, т.е. r (A) =r (A1)= 3 Þ система совместна.
1) Исследуя систему на совместность, расширенную матрицу преобразовали по методу Гаусса. Метод Гаусса состоит в следующем: 1. Приведение матрицы к треугольному виду, т. е. ниже главной диагонали должны находиться нули (прямой ход). 2. Из последнего уравнения находим х3 и подставляем его во второе, находим х2, и зная х3, х2 подставляем их в первое уравнение, находим х1 (обратный ход). Запишем, преобразованную по методу Гаусса, расширенную матрицу
в виде системы трех уравнений:
х2=х3 Þ х3=1 2х1=4+х2+х3 Þ 2х1=4+1+1 Þ Þ 2х1=6 Þ х1=3 Ответ: х1=3, х2=1, х3=1. 2) Решим систему по формулам Крамера: если определитель системы уравнений Δ отличен от нуля, то система имеет единственное решение, которое находится по формулам
Вычислим определитель системы Δ:
Находим по формулам неизвестные:
Ответ: х1=3, х2=1, х3=1 . 3) Решим систему средствами матричного исчисления, т. е. при помощи обратной матрицы. А×Х=В Þ Х=А-1× В, где А-1 – обратная матрица к А,
Обратная матрица считается по формуле:
где D - определитель матрицы А, Аij – алгебраические дополнения элемента а ij матрицы А. D = 60 (из предыдущего пункта). Определитель отличен от нуля, следовательно, матрица А обратима, и обратную к ней матрицу можно найти по формуле (*). Найдем алгебраические дополнения для всех элементов матрицы А по формуле: Аij= (-1) i+j Mij .
Запишем обратную матрицу.
Сделаем проверку по формуле: А-1× А=Е.
А-1А =
Вывод: так как произведение А-1× А дает единичную матрицу, то обратная матрица А-1 найдена верно и решение системы определяется по формуле Х=А-1×В.
Ответ: х1=3, х2=1, х3=1. Проверка. Подставим полученные значения в систему. Получим:
Т. к. неизвестные х1, х2, х3 обратили каждое уравнение в тождество, то они найдены верно.
Пример 6. Решить систему методом Гаусса и найти какие-нибудь два базисных решения системы.
Решение:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.113 (0.009 с.) |

 ; б)
; б) 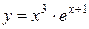 .
. ; б)
; б)  .
. ; б)
; б) 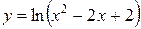 .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
.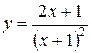 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ,
,  ,
,  ,
,  в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы  ,
,  ,
,  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора  в этом базисе.
в этом базисе. , необходимо и достаточно, чтобы они были линейно независимы. Это значит, определитель, столбцами которого являются координаты векторов системы, должен быть отличен от нуля.
, необходимо и достаточно, чтобы они были линейно независимы. Это значит, определитель, столбцами которого являются координаты векторов системы, должен быть отличен от нуля. .
. .
. по базису
по базису  ,
, .
.


 ;
;  ;
;  .
.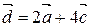 или
или  = 2 (2; 4; 1)+ 4 (5; 3; 1;)=(4; 8; 2)+(20; 12; 4)=(24; 20; 6)=
= 2 (2; 4; 1)+ 4 (5; 3; 1;)=(4; 8; 2)+(20; 12; 4)=(24; 20; 6)=  . Значит, разложение вектора
. Значит, разложение вектора  , то длина ребра - это длина вектора. Находим координаты вектора
, то длина ребра - это длина вектора. Находим координаты вектора 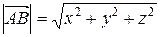 .
. .
. . Находим координаты вектора
. Находим координаты вектора  .
. .
.
 .
.

 ,
, =(l,m,n) – координаты направляющего вектора прямой М1М2.
=(l,m,n) – координаты направляющего вектора прямой М1М2. .
.

 , (*)
, (*) .
. - алгебраические дополнения элементов
- алгебраические дополнения элементов  , а Мi j – минор элемента
, а Мi j – минор элемента 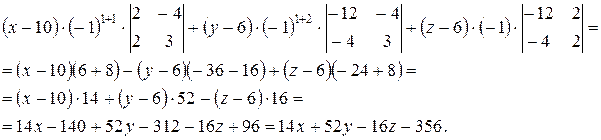
 .
. .
. ,
, - координаты нормального вектора плоскости АВС.
- координаты нормального вектора плоскости АВС. - координаты направляющего вектора прямой АD.
- координаты направляющего вектора прямой АD. .
. ,
, 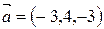 .
. , то ее нормальный вектор
, то ее нормальный вектор  .
. .
. .
. , то его площадь считается по формуле:
, то его площадь считается по формуле: .
.


 .
. .
. объема параллелепипеда, построенного на векторах
объема параллелепипеда, построенного на векторах  ,
,  ,
,  ,
,  .
.
 .
. . Для того, чтобы составить уравнение высоты, надо знать направляющий вектор
. Для того, чтобы составить уравнение высоты, надо знать направляющий вектор  (
( - перпендикулярен АВС). Следовательно, в качестве направляющего вектора прямой DHможно взять нормальный вектор плоскости АВС. Т.е.
- перпендикулярен АВС). Следовательно, в качестве направляющего вектора прямой DHможно взять нормальный вектор плоскости АВС. Т.е.  . Уравнение высоты имеет вид:
. Уравнение высоты имеет вид: .
. .
. .
. .
. Þ
Þ  Þ
Þ  .
. .
.
 Þ
Þ  Þ
Þ  .
. . Две прямые перпендикулярны, если:
. Две прямые перпендикулярны, если:  . Т. к. АС ^ ВН, то
. Т. к. АС ^ ВН, то  .
. .
. Þ 4 (у+6)=7(х+2) Þ 4 у+24=7х+14.
Þ 4 (у+6)=7(х+2) Þ 4 у+24=7х+14. . Тогда получим
. Тогда получим
 .
.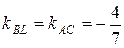 и точку B(-2;-6), через которую проходит эта прямая, т. е.
и точку B(-2;-6), через которую проходит эта прямая, т. е. .
.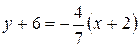 Þ7 у+42=-4х-8 Þ BL: 4х+7у+50=0.
Þ7 у+42=-4х-8 Þ BL: 4х+7у+50=0. Þ
Þ 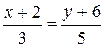 . 5(х +2) = 3(у +6) Þ 5 х+10 = 3 у +18Þ АВ: 5х-3у-8=0.
. 5(х +2) = 3(у +6) Þ 5 х+10 = 3 у +18Þ АВ: 5х-3у-8=0. . Знаем, что
. Знаем, что  .
. .
.
 .
.
 .
. - точка пересечения стороны АС и высоты ВН. Эта же точка является серединой отрезка ВВ1. Зная формулы координат середины отрезка
- точка пересечения стороны АС и высоты ВН. Эта же точка является серединой отрезка ВВ1. Зная формулы координат середины отрезка ,
,
 Окончательно имеем:
Окончательно имеем:  .
.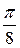 ;
; .
.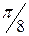














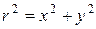 и
и  .
. .
. ;
; ,
,  ;
;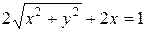 .
. .
. - парабола.
- парабола. , ветви направлены влево.
, ветви направлены влево.
 ,
,  .
.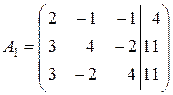 .
. ~
~ ~
~
 ~
~ 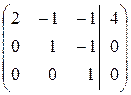 ;
;  ~
~  .
. .
. Þ х3=1
Þ х3=1 ;
;  ;
;  .
. Т.к. определитель системы отличен от нуля, то согласно правилу Крамера, система имеет единственное решение. Вычислим определители Δ1, Δ2, Δ3. Они получаются из определителя системы Δ заменой соответствующего столбца на столбец свободных коэффициентов.
Т.к. определитель системы отличен от нуля, то согласно правилу Крамера, система имеет единственное решение. Вычислим определители Δ1, Δ2, Δ3. Они получаются из определителя системы Δ заменой соответствующего столбца на столбец свободных коэффициентов.
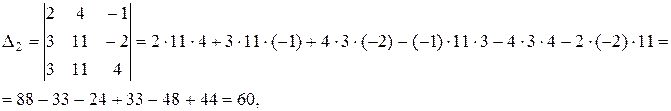

 ;
;  ;
; 
 - столбец свободных членов,
- столбец свободных членов, - матрица-столбец неизвестных.
- матрица-столбец неизвестных. (*)
(*)








 .
.
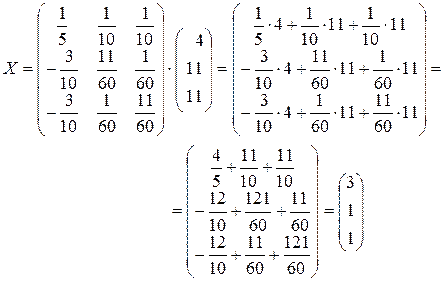 .
.




