
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование неявных и параметрических заданных функций.Содержание книги
Поиск на нашем сайте
Логарифмическое дифференцирование. Литература. [2], Гл. III, § 11-12, 16, 18; [3], Гл. V, § 5-3 задачи 206-211. Можно использовать также [6], Гл. V, § 21, 22; [7], Гл. VII, § 1, задачи 7.1.58., 7.1.65., 7.1. 72.; [5], Гл. VII, § 1 задачи 768-770, 896-897, 908. Производная высших порядков. Литература. [2], Гл. III, § 22; [3], Гл. V, § 4 задачи 162-191. Можно использовать также [6], Гл. V, § 23; [7], Гл. VII, § 1, задачи 7.1.83.; [5], Гл. VII, § 1 задачи 945-949. Дифференциал функции. Литература. [2], Гл. III, § 20, 23; [3], Гл. V, § 3-4 задачи 146-161, 198-205. Можно использовать также [6], Гл. V, § 24; [7], Гл. VII, § 2, задачи 7.2.1., 7.2.9., 7.2.13.; [5], Гл. VII, § 1 задачи 975-981; [3], Гл. V, § 3, 4., разобрать примеры 1-2, 3.
При вычислении производных используется таблица производных элементарных функций, применяются правила дифференцирования суммы, разности, произведения и частного функций, а также правило дифференцирования сложной функции.
Примеры решения типовых задач
№ 8. Найти производную указанного порядка:
1)
=
2) Найти производную второго порядка от функции, заданной параметрически.
Найдем первую производную
Найдем вторую производную
Задания контрольной работы № 1
1 - 25. Даны координаты вершин пирамиды А1А2А3А4. Найти: 1) длину ребра А1 А2; 2) угол между ребрами А1 А2 и А1 А4; 3) угол между ребром А1 А4 и гранью А1 А2 А3; 4) площадь грани А1 А2 А3; 5) объем пирамиды; 6) уравнение прямой А1 А2; 7) уравнение плоскости А1 А2 А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
1. А1 (-1; 2; 1), А2 (-2; 2; 5), А3 (-3; 3; 1), А4 (-1; 4; 3). 2. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1). 3. А1 (4; 2; 5), А2 (0; 7; 2), А3 (0; 2; 7), А4 (1; 5; 0). 4. А1 (4; 4; 10), А2 (-4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9). 5. А1 (-2; 1; -1), А2 (-3; 1; 3), А3 (-4; 2; -1), А4 (-2; 3; 1). 6. А1 (1; 1; 2), А2 (0; 1; 6), А3 (-1; 2; 2), А4 (1; 3; 4). 7. А1 (-1; -2; 1), А2 (-2; -2; 5), А3 (-3; -1; 1), А4 (-1; 0; 3). 8. А1 (2; -1; 1), А2 (1; -1; 5), А3 (0; 0; 1), А4 (2; 1; 3). 9. А1 (-1; 1; -2), А2 (-2; 1; 2), А3 (-3; 2; -2), А4 (-1; 3; 0). 10. А1 (4; 6; 5), А2 (6; 9; 4), А3 (2; 10; 10), А4 (7; 5; 9). 11. А1 (3; 5; 4), А2 (8; 7; 4), А3 (5; 10; 4), А4 (4; 7; 8). 12. А1 (10; 6; 6), А2 (-2; 8; 2), А3 (6; 8; 9), А4 (7; 10; 3). 13. А1 (1; 8; 2), А2 (5; 2; 6), А3 (5; 7; 4), А4 (4; 10; 9). 14. А1 (6; 6; 5), А2 (4; 9; 5), А3 (4; 6; 11), А4 (6; 9; 3). 15. А1 (7; 2; 2), А2 (5; 7; 7), А3 (5; 3; 1), А4 (2; 3; 7). 16. А1 (8; 6; 4), А2 (10; 5; 5), А3 (5; 6; 8), А4 (8; 10; 7). 17. А1 (1; 2; 1), А2 (0; 2; 5), А3 (-1; 3; 1), А4 (1; 4; 3). 18. А1 (-2; -1; 1), А2 (-3; -1; 5), А3 (-4; 0; 1), А4 (-2; 1; 3). 19. А1 (1; -1; 2), А2 (0; -1; 6), А3 (-1; 0; 2), А4 (1; 1; 4). 20. А1 (1; -2; 1), А2 (0; -2; 5), А3 (-1; -1; 1), А4 (1; 0; 3). 21. А1 (0; 3; 2), А2 (-1; 3; 6), А3 (-2; 4; 2), А4 (0; 5; 4). 22. А1 (-1; 2; 0), А2 (-2; 2; 4), А3 (-3; 3; 0), А4 (-1; 4; 2). 23. А1 (2; 2; 3), А2 (1; 2; 7), А3 (0; 3; 3), А4 (2; 4; 5). 24. А1 (0; -1; 2), А2 (-1; -1; 6), А3 (-2; 0; 2), А4 (0; 1; 4). 25. А1 (3; 0; 2), А2 (2; 0; 6), А3 (1; 1; 2), А4 (3; 2; 4). 26 –50. Решить задачу.
26. Даны уравнения одной из сторон ромба х – 3 у + 10 = 0 и одной из его диагоналей х + 4 у – 4 = 0; диагонали ромба пересекаются в точке (0; 1). Найти уравнения остальных сторон ромба.
27. Найдите точку, равноудаленную от трех данных точек: А (2; 2), В (-5; 1), С (3; -5). Составить уравнение ВС.
28. Дан треугольник АВС с вершинами А (-4; -5), В (8; 1) и С (2; -8). Найдите точку пересечения биссектрисы угла А с противолежащей стороной, вычислите ее длину, составьте ее уравнение.
29. Найдите уравнение прямой, проходящей через точку (2/3; 8/3) и точку пересечения прямых 3 х - 5 у – 11 = 0 и 4 х + у – 7 = 0.
30. Даны вершины А (-3; -2), В (4; -1), С (1; 3) трапеции АВСД (АД || ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины Д этой трапеции.
31. Дан треугольник АВС с вершинами А (5; 3), В (-1; 3), С (2; 0). Из точки Д, делящей сторону ВС в отношении | ВД |: | ДС | = 2: 1, проведена прямая через середину Е стороны АВ. Найдите уравнение и длину ДЕ.
32. Даны уравнения двух высот треугольника х + у = 4 и у = 2 х и одна из его вершин А (0; 2). Составить уравнения сторон треугольника.
33. До какой точки надо продолжить отрезок АВ из точки А (-2; -3) в точку В (2; 3), чтобы | АВ |: | ВС | = 1: 3? Составьте уравнение перпендикуляра, восстановленного из точки С.
34. Докажите, что средняя линия треугольника АВС с вершинами А (2; 4), В (-1; -2), С (6; -1) параллельна стороне ВС. Составьте уравнение и найдите ее длину.
35. Определить координаты вершин треугольника, если известны уравнения его сторон: 2 х - у – 3 = 0, 2 х + 3 у + 13 = 0, х - 2 у + 3=0. Найдите внутренний угол АВС в треугольнике.
36. Дан треугольник АВС с вершинами А (-5; 4), В (4; -3), С (-2; -6). Найти расстояние от вершины А до стороны ВС.
37. Составьте уравнение прямой, проходящей через точку пересечения прямых 3 х - 2 у – 12 = 0 и х + 2 у + 4 = 0 и перпендикулярно прямой 2 х - 3 у + 6 = 0.
38. Известны уравнения двух сторон ромба 2 х + у = 4 и 2 х + у = 10 и уравнение одной из его диагоналей х - у - 2 = 0. Найти уравнения остальных сторон ромба.
39. Дан треугольник АВС с вершинами А (3; 4), В (-3; -4), С (-9; 13). Доказать, что треугольник АВС прямоугольный, вычислить длину высоты АД.
40. Даны две вершины треугольника АВС: А (2; - 3) и В (5; 1), уравнение стороны ВС: у - 1 = 0 и медианы АМ: 2 х – у - 7 = 0. Составить уравнения остальных сторон треугольника и уравнение высоты, опущенной из вершины С на сторону АВ.
41. Даны две точки В (3; 1) и С (-5; 5). Найти расстояние от середины отрезка ВС до прямой 2 х - 3 у - 6 = 0.
42. Дано: уравнение прямой х + 2 у - 4 = 0 и точка А (-2; -3). Найти длину отрезка АС и составить уравнение прямой, проходящей через точки А и С, где точка С – середина отрезка прямой, заключенного между осями координат.
43. Уравнения двух сторон параллелограмма х + 2 у + 2 = 0 и х + у + 4 = 0, а уравнение одной из его диагоналей х – 2 = 0. Найти координаты вершин параллелограмма.
44. Даны две вершины треугольника АВС: А (-10; 2) и В (6; 4), его высоты пересекаются в точке N (5; 2). Определить координаты третьей вершины С.
45. Даны три точки А (5; 2), В (2; 1), С (6; 4). Найти угол между прямыми АВ и АС. 46. В треугольнике АВС даны уравнение стороны АВ: 5 х – 3 у + 2 = 0, уравнения высот АN: 4 х – 3 у + 1 = 0 и ВМ: 7 х + 2 у - 22 = 0. Составить уравнения двух других сторон и третьей высоты этого треугольника.
47. Даны две вершины А (2; -2) и В (3; -1) и точка Р (1; 0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С.
48. Дан треугольник АВС с вершинами А (-3; 2), В (2; 3), С (4; -2). Составьте уравнение прямой, проходящей через точку пересечения медиан треугольника, параллельно прямой 2 х - 3 у - 6 = 0.
49. Даны три последовательные вершины параллелограмма А (1; -2), В (3; 2), С (6; 4).Найти координаты четвертой вершины Д и уравнение стороны АВ.
50. Вычислите угол между прямыми
51 – 75. Установить, какие линии определяются данными уравнениями. Изобразить эти линии на чертеже, охарактеризовав кривые.
51.
52.
53. Составить уравнение и построить линию, расстояние каждой точки которой от точки А (-1; 0) вдвое меньше расстояния ее от прямой х = - 4.
54.
55.
56. Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки А (5; 0) относятся, как 2: 1
57. 58.
59. Составить уравнение и построить линию, расстояния каждой точки которой от точки А (2; 0) и от прямой 5 х + 6 = 0относятся, как 5: 4.
60.
61.
62. Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А (4; 0), чем от точки Е (1; 0). 63.
64.
65. Составить уравнение и построить линию, расстояния каждой точки которой от точки А (2; 0) и от прямой 2 х + 5 = 0относятся, как 4:5.
66.
67.
68. Составить уравнение и построить линию, расстояние каждой точки которой от точки А (3; 0) вдвое меньше расстояния от точки В (28; 0).
69.
70.
71. Составить уравнение и построить линию, каждая точка которой одинаково удалена от точки А (0; 2) и от прямой у - 4 = 0.
72.
73.
74. Составить уравнение и построить линию, каждая точка которой отстоит от точки А (-4; 0) втрое дальше, чем от начала координат.
75.
76 – 100. Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса и методом Крамера.
76.
78.
80.
82.
84.
86.
88.
90.
92.
94. 96.
98.
100.
101 – 125. Найти матрицу обратную матрице: Сделать проверку.
101.
103.
105.
107.
109.
111.
113.
115.
117.
119.
121.
123.
125.
126 – 150. Вычислить пределы функций, не пользуясь правилом Лопиталя.
126. а) в)
127. а) в)
128. а) в)
129. а) в)
130. а) в)
131. а) в)
132. а) в)
133. а) в)
134. а) в)
135. а) в)
136. а) в)
137. а) в)
138. а) в)
139. а) в)
140. а) в)
141. а) в)
142. а) в)
143. а) в)
144. а) в)
145. а) в)
146. а) в)
147. а) в)
148. а) в)
149. а) в)
150. а) в)
151 – 175. Задана функция у = f (x):
1) Исследовать функцию на непрерывность на всей числовой оси. 2) Найти и классифицировать точки разрыва, если они существуют. 3) Построить график функции.
151. f (x) =
153. f (x) =
155. f (x) =
157. f (x) =
159. f (x) =
161. f (x) =
163. f (x) =
165. f (x) =
167. f (x) =
169. f (x) =
171. f (x) = 173. f (x) =
175. f (x) =
176 – 200. Найти а)
176. а)
177. а)
178. а)
179. а)
180. а)
181. а)
182. а)
183. а)
184. а)
185. а)
186. а)
187. а)
188. а)
189. а)
190. а)
191. а)
192. а) 193. а)
194. а)
195. а)
196. а)
197. а)
198. а)
199. а)
200. а)
Основные формулы 1. |
2. Формулы деления отрезка в данном отношении:
3. Линейные операции над векторами в координатной форме:
·
·
·
· коллинеарность векторов: 4. Формула скалярного произведения
5. Скалярное произведение в координатной форме 6. Формула для нахождения угла между векторами cos (
7. Векторное произведение в координатной форме
8.
9. Sпар. = | 10. Смешанное произведения векторов в координатной форме
11.
12. Объем параллелепипеда: V = |
Объем треугольной пирамиды: V = 13. Ах + By + С = 0 - общее уравнение прямой, где А, В, С – произвольные числа.
14. Уравнение прямой, проходящей через данную точку мо (хо; уо)с направляющим вектором (с; d)
15. Уравнение прямой, проходящей через две точки М1 (x1; y1)и М2 (x2; y2)
16. А (х - х0) + В (у – у0) = 0 - уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору, где (А; В)координаты нормального вектора прямой, (х0; у0) координаты текущей точки,а х и у переменные.
17. Формула для нахождения расстояния от точки (х 1; у 1) до прямой Ах + By + С = 0:
18. (х + х 0)2 + (у + у 0)2 = r 2– каноническое уравнение окружности с центром в точке (х 0; у 0), радиусом r. 19.
20. 21. Канонические уравнения парабол: у2 = 2рх, у2 = —2рх, х2 = 2ру, х2 = —2ру (р > 0)
22. Основные теоремы о пределах: · · · · · |
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 295; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.196.150 (0.014 с.) |




 ;
;


 ;
; х х =
х х = 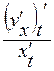
 х:
х: 

 t = 3 t 2,
t = 3 t 2,  .
.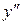 х х =
х х =  =
=  .
. х - у + 2 = 0 и
х - у + 2 = 0 и 













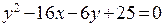


 77.
77. 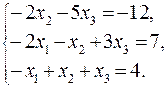
 79.
79. 
 81.
81. 
 83.
83. 
 85.
85. 
 87.
87. 
 89.
89. 
 91.
91. 
 93.
93. 
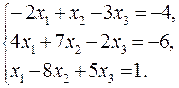 95.
95. 
 97.
97. 
 99.
99. 

 .
. 102.
102. 
 104.
104. 
 106.
106. 
 108.
108. 
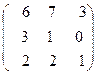 110.
110. 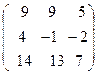
 112.
112. 
 114.
114. 
 116.
116. 
 118.
118. 
 120.
120. 
 122.
122. 
 124.
124. 

 ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
;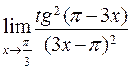 ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г) 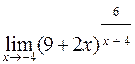 .
. ; б)
; б) 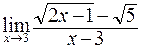 ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г) 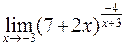 .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б) 
 ; г)
; г)  .
. ; б)
; б) 
 ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
.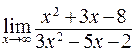 ; б)
; б)  ;
; ; г)
; г)  .
.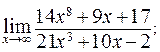 б)
б)  ;
; 
 ; г)
; г)  .
. ; б)
; б)  ;
;  ; г)
; г)  .
. ; б)
; б)  ;
;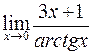 ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
;  ; г)
; г)  .
. 152. f (x) =
152. f (x) = 
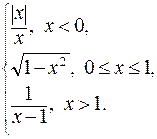 154. f (x) =
154. f (x) = 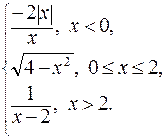
 156. f (x) =
156. f (x) = 
 158. f (x) =
158. f (x) = 
 160. f (x) =
160. f (x) = 
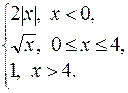 162. f (x) =
162. f (x) = 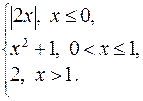
 164. f (x) =
164. f (x) = 
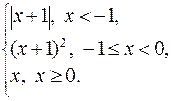 166. f (x) =
166. f (x) = 
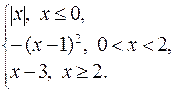 168. f (x) =
168. f (x) = 
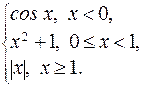 170. f (x) =
170. f (x) = 
 172. f (x) =
172. f (x) = 
 174. f (x) =
174. f (x) = 
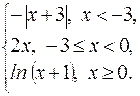
 и
и 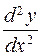 для заданных функций:
для заданных функций: ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
, 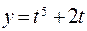 .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б) 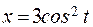 ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
, 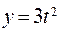 .
. ; б)
; б) 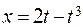 ,
, 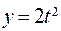 .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
.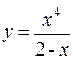 ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б) 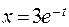 ,
,  .
. ; б)
; б)  ,
,  .
. ; б)
; б) 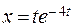 ,
,  .
.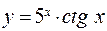 ; б)
; б)  ,
,  .
. ; б)
; б)  ,
,  .
. | =
| = 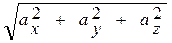 - модуль вектора
- модуль вектора ,
, 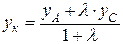 , где
, где  - отношение
- отношение  .
. = (bx; bу; bz)
= (bx; bу; bz)


 .
. = |
= |  | * |
| * | 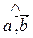 )
)



 (и наоборот), т.е.
(и наоборот), т.е.  =
=  =
= 
 |
|  =
= 

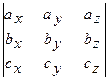 = 0
= 0  векторы
векторы  |
| 

 .
. - каноническим уравнением эллипса.
- каноническим уравнением эллипса. - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы. f(х) = А, то он единственный.
f(х) = А, то он единственный.


