
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Указания к выполнению контрольной работы 1Содержание книги
Поиск на нашем сайте
Тема 1. Элементы линейной алгебры и аналитической геометрии
Матрицы, операции над ними. Определители Литература. [1], Гл. X, § 1, 2.; [3], Гл. VII, § 1 разобрать пример № 1. Можно использовать также [6], Гл. I, § 1-3.; [7], Гл. I, § 1, 2 задачи 1.1.1., 1.1.5., 1.2.13., 1.4.1.; [5], Гл. IV, § 2 задачи 400-403. Системы линейных уравнений. Правило Крамера Литература. [1], Гл. X, § 3, 4.; [3], Гл. VII, § 2 разобрать примеры № 1-2. Можно использовать также [6], Гл. I, § 4.; [7], Гл. II, § 1-3 задачи 2.1.2., 2.2.2. Векторы Литература. [1], Гл. III, § 1-4, Гл. IX, § 1-5.; [3], Гл. III, § 1-4 задачи 1-5, 16-18, 22-24, 38-40, 42-47; Гл. X, § 1-3 задачи 6-14, 22-33. Можно использовать также [6], Гл. II, § 5.; [7], Гл. III, § 1 задачи 3.1.1., 3.1.13.-3.1.20. Скалярное произведение векторов Литература. [1], Гл. IX, § 6.; [3], Гл. X, § 4 задачи 41-51. Можно использовать также [6], Гл. II, § 6.; [7], Гл. III, § 2 задачи 3.2.1., 3.2.4., 3.2.8. Векторное произведение векторов Литература. [1], Гл. IX, § 7.; [3], Гл. X, § 5 задачи 63-73. Можно использовать также [6], Гл. II, § 7.; [7], Гл. III, § 3 задачи 3.3.1., 3.3.5., 3.3.9. Смешанное произведение векторов Литература. [1], Гл. IX, § 8.; [3], Гл. X, § 6 задачи 83-88, 98-100. Можно использовать также [6], Гл. II, § 8.; [7], Гл. III, § 4 задачи 3.4.1., 3.4.4.
Линии на плоскости и в пространстве Литература. [1], Гл. III, § 5-6, Гл. IX, § 9-13.; [3], Гл. III, § 5-7 задачи 52-54, 59-67, 68-85; Гл. X, § 7-9 задачи 101-103, 114-122,130-138, 153-162, 165-168, 172-181. Можно использовать также [6], Гл. III, § 10.; [7], Гл. IV, § 1-2 задачи 4.2.1., 4.2.6., 4.2.8., 4.2.57., 4.2.67., 4.2.68. Линии второго порядка Литература. [1], Гл. III, § 7-8, Гл. IX, § 9-14.; [3], Гл. III, § 8 задачи 126-132, 139-147, 150-155.; Гл. X, § 10 задачи 166-171. Можно использовать также [6], Гл. III, § 11.; [7], Гл. IV, § 3 задачи 4.3.1., 4.3.28., 4.3.31., 4.3.60., 4.3.64., 4.3.105, 4.3.106. Уравнения поверхности и линии в пространстве Литература. [4], Гл. III, § 3.1-3.4; [4], Гл. III, § 3.1-3.4 задачи 1-28;[6], Гл. IV, § 12.; [7], Гл. V, § 1-5 задачи 5.1.1., 5.1.29., 5.2.6., 5.2.7., 5.2.12., 5.2.41, 5.3.1., 5.3.5., 5.3.7., 5.3.25., 5.4.3., 5.4.8., 5.5.1., 5.5.4., 5.5.14., 5.5.15., 5.5.17.
Примеры решения типовых задач № 1. Даны координаты вершин пирамиды А1 А2 А3 А4. А1 (0; 2; - 2), А2 (1; 0; - 1), А3 (0; 5; - 1), А4 (0; 2; 1). Найти: 1) длину ребра А1 А2; 2) угол между ребрами А1 А2 и А1 А4; 3) угол между ребром А1 А4 и гранью А1 А2 А3; 4) площадь грани А1 А2 А3; 5) объем пирамиды; 6) уравнение прямой А1 А2; 7) уравнение плоскости А1 А2 А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж. Решение 1. Найти длину ребра А1 А2.
2. Найти угол между ребрами А1 А2 и А1 А4.
где
3. Найти угол между ребром А1 А4 и гранью А1 А2 А3. Угол между ребром А1 А4 и гранью А1 А2 А3 вычисляется по формуле: Составим уравнение плоскости (А1 А2 А3). Воспользуемся уравнением плоскости, проходящей через три заданные точки А1 (0; 2; -2), А2 (1; 01; -1) и А3 (0; 5; -1) имеет вид:
отсюда 4. Найти площадь грани А1 А2 А3. Найдем векторное произведение векторов S параллелограмма
Площадь треугольника равна половине площади параллелограмма, т.е. S треугольника = 5. Найти объем пирамиды А1 А2 А3 А4. Объем пирамиды равен одной шестой модуля смешанного произведения трех векторов, т.е.
6. Составить уравнение прямой А1 А2.
7. Составить уравнение плоскости А1 А2 А3.
(Решение см. в пункте 3). 8. Составить уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3.
z
0 y А2 А3 x А1
№ 2. а) Дан треугольник АВС с вершинами А (-5; 4), В (3; -2), С (-8; -5). Составить уравнение медианы СК и высоты АН.
Решение 1) А (х - х0) + В (у – у0) = 0, где (А; В) координаты нормального вектора прямой СК, (х0; у0) – координаты точки С (-8; -5). Найдем координаты точки К.
6(х + 8)- 7(у + 5) = 0 6 х - 7 у + 13 = 0 - уравнение медианы СК.
2) А (х - х0) + В (у – у0) = 0, где (А; В) координаты нормального вектора прямой АН, (х0; у0) – координаты точки А (-5; 4). Нормальным вектором прямой АН является вектор 11(х + 5)+ 3(у - 4) = 0 11 х + 3 у + 43 = 0 - уравнение высоты АН.
А (-5; 4)
К
х В (3; -2)
Н С (-8; -5).
б) Даны две последовательные вершины параллелограмма А (- 5; 3) и В (2; 7), точка пересечения его диагоналей К (- 1; 2). Найти остальные вершины параллелограмма.
Решение 7 В
А 3 К С х - 5 - 4 - 1 3
Д - 3
Для нахождения координат точки С воспользуемся формулами деления отрезка в данном отношении:
Для нахождения координат точки Д воспользуемся формулами деления отрезка в данном отношении:
№ 3. Установить, какая линия определяется данным уравнением. Изобразить данную линию на чертеже, охарактеризовав ее. а) х 2 + у 2 + 6 х +10 у – 15 = 0. Преобразуем данное уравнение: х 2 + 6 х + 9 + у 2 + 10 у – 9 – 25 - 15 = 0;
(х +3)2 + (у + 5)2 - 49 = 0 – уравнение окружности с центром в точке (- 3; - 5), радиусом 7.
х
О (- 3; - 5)
б) 9 х 2 + 16 у 2 = 144. Разделим обе части уравнения на 144:
Координаты вершин эллипса: А 1,2 ( А 1,2 ( Большая ось эллипса | А 1 А 2| = 2 а = 8, малая ось эллипса | В 1 В 2| = 2 b = 6. Определим координаты фокусов (фокусы эллипса находятся на большой оси), для этого воспользуемся формулой с 2 = а 2 - b 2;
Координаты фокусов: F 1,2 ( F 1,2 (
Построим график эллипса у В 1 3
А 2 F 2 F 1 А 1
- 4 -
- 3 В 2 в) 25 х 2 - 9 у 2 - 100 х – 54 у – 206 = 0. Преобразуем данное уравнение:
(25 х 2 - 100 х)– (9 у 2 + 54 у) – 206 = 0; 25(х 2 - 4 х)– 9(у 2 + 6 у) – 206 = 0; 25(х 2 - 4 х + 4)– 100 – 9(у 2 + 6 у + 9) + 81 –206 = 0; 25(х – 2)2 – 100 – 9(у + 3)2 + 81 – 206 = 0; 25(х – 2)2 – 9(у + 3)2 – 225 = 0; 25(х – 2)2 – 9(у + 3)2 = 225;
а 2 = 9, b 2 = 25, значит, а = 3, b = 5. Центр гиперболы находится в точке (2; - 3) Координаты вершин гиперболы: действительные вершины: А 1 (5; - 3), А 2 (- 1; - 3), мнимые вершины: В 1 (2; 2), В 2 (2; - 8). Действительная ось гиперболы | А 1 А 2| = 2 а = 6, мнимая ось гиперболы | В 1 В 2| = 2 b = 10. Определим координаты фокусов (фокусы гиперболы находятся на действительной оси), для этого воспользуемся формулой с 2 = а 2 + b 2;
Координаты фокусов: F 1 (5 +
Построим график гиперболы В 1
- 3 - 1 2 х F 2 А 2 А 1 F 1
- 8 В 2 г) х = 1 - Преобразуем данное уравнение: х - 1 = - (х – 1)2 = (-
Построим график параболы:
№ 4. Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса и методом Крамера. Метод Крамера.
1. Найдем определитель данной системы: 2. Найдем определители
3. Находим значения неизвестных
4. Делаем проверку:
Ответ: Метод Гаусса. Составим матрицу из коэффициентов перед неизвестными переменными и свободных членов.
Приведем матрицу к треугольному виду. Поменяем в матрице первую и вторую строки, для того, чтобы на первом месте была единица.
зафиксируем первую строку, домножим ее на «-2», суммируя результат со второй строкой; результат записать на место второй строки;
домножим ее на «-3», суммируя результат с третьей строкой; результат записать на место третьей. ~
~ ~
Ответ:
№ 5. Найти обратную матрицу, выполнить проверку: Пусть дана матрица 1) Вычисляем определитель матрицы А: 2) Находим алгебраические дополнения элементов этого определителя:
3) Записываем обратную матрицу:
4) Выполнить проверку:
= = Ответ:
Тема 2. Введение в математический анализ
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.230.81 (0.012 с.) |


 (ед)
(ед) , отсюда
, отсюда ,
, и
и  .
. и
и  ,
,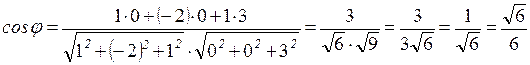 , значит
, значит 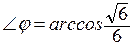 .
. , где
, где  - нормальный вектор плоскости (А1 А2 А3).
- нормальный вектор плоскости (А1 А2 А3). 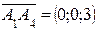 .
.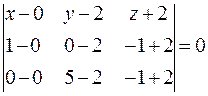 ;
; 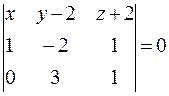 ;
; ;
; ;
;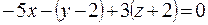 ;
; (умножим на - 1);
(умножим на - 1);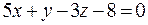 - уравнение плоскости А1 А2 А3.
- уравнение плоскости А1 А2 А3.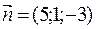 - нормальный вектор плоскости А1 А2 А3.
- нормальный вектор плоскости А1 А2 А3. ,
, .
.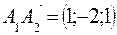 и
и 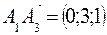 .
. ,
, 


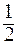
 (ед 2).
(ед 2). ,
, .
.
 - направляющий вектор прямой
- направляющий вектор прямой 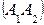 , точка
, точка  лежит на прямой. Тогда каноническое уравнение прямой
лежит на прямой. Тогда каноническое уравнение прямой  имеет вид:
имеет вид:  ,
, 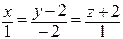 .
. - уравнение плоскости А1 А2 А3.
- уравнение плоскости А1 А2 А3.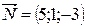 - нормаль плоскости А1 А2 А3. Высота опущенная из вершины А4 (0; 2; 1) на грань А1 А2 А3 перпендикулярна к ней.
- нормаль плоскости А1 А2 А3. Высота опущенная из вершины А4 (0; 2; 1) на грань А1 А2 А3 перпендикулярна к ней.
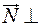 (А1 А2 А3) и высота А4H
(А1 А2 А3) и высота А4H  (А1 А2 А3), следовательно
(А1 А2 А3), следовательно 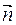 ||(А4H). Вектор
||(А4H). Вектор  является направляющим вектором высоты А4H. Тогда каноническое уравнение прямой
является направляющим вектором высоты А4H. Тогда каноническое уравнение прямой  имеет вид:
имеет вид: 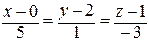 ,
,  .
. А4
А4

 ;
; 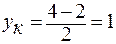 ; К (-1;1);
; К (-1;1);  = (7; 6); нормальный вектор прямой СК имеет координаты (6; -7).
= (7; 6); нормальный вектор прямой СК имеет координаты (6; -7).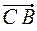 = (11; 3).
= (11; 3). у
у
 ,
, 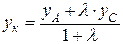 , где
, где  - отношение
- отношение  ,
,  и
и  .
. ,
,  . С (3; 1).
. С (3; 1). ,
,  , где
, где  ,
, 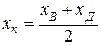 и
и  .
. ,
,  . Д (- 4; - 3).
. Д (- 4; - 3).

 у
у (каноническое уравнение эллипса
(каноническое уравнение эллипса  ), а 2 = 16, b 2 = 9, значит, а = 4, b = 3.
), а 2 = 16, b 2 = 9, значит, а = 4, b = 3. а; 0), В 1,2 (0;
а; 0), В 1,2 (0;  .
.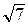 ; 0).
; 0). Эксцентриситет эллипса
Эксцентриситет эллипса  (для случая b > а,
(для случая b > а,  ).
).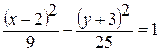 – каноническое уравнение гиперболы со смещенным центром
– каноническое уравнение гиперболы со смещенным центром 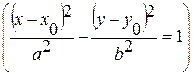 .
. .
. ; - 3), F 2 (2 -
; - 3), F 2 (2 -  Эксцентриситет эллипса
Эксцентриситет эллипса 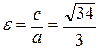 (для случая
(для случая 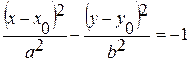 ,
,  .
. ;
;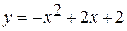 - общее уравнение параболы, с вершиной в точке (1; 3), направлением ветвей вниз, с осью симметрии х = 1.
- общее уравнение параболы, с вершиной в точке (1; 3), направлением ветвей вниз, с осью симметрии х = 1.


 ;
; .
. , где
, где  получен из
получен из 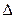 путём замены первого столбца на столбец свободных членов, остальные определители находятся аналогично.
путём замены первого столбца на столбец свободных членов, остальные определители находятся аналогично.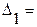
 ,
, 
 ,
, 
 .
. :
: 
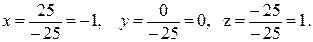
 ;
;  ;
;  .
.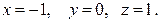

 ~
~ ~ поменяем вторую и третью строки местами
~ поменяем вторую и третью строки местами ~ разделим вторую строку на 3, а третью на «-5»
~ разделим вторую строку на 3, а третью на «-5»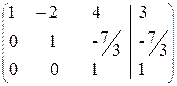 получаем систему
получаем систему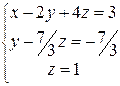 ,
, 
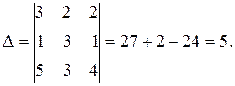


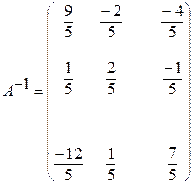
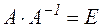 .
.

 =
= =
= =
= 



