
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Худякова С.А., Бараховская О.В.Содержание книги
Поиск на нашем сайте
ВЫСШАЯ МАТЕМАТИКА Методические указания и варианты контрольной работы № 1 для слушателей факультета заочного обучения по специальности 280104.65 – Пожарная безопасность 1 год обучения
Екатеринбург
Худякова С.А., Бараховская О.В. Высшая математика: Методические указания и варианты контрольной работы № 1 для слушателей факультета заочного обучения по специальности 280104.65 – Пожарная безопасность. 1 год обучения. – Екатеринбург: ГОУ ВПО «УРАЛЬСКИЙ ИНСТИТУТ ГОСУДАРСТВЕННОЙ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ», 2007. – 48 с.
Методические указания предназначены слушателям заочного обучения по специальности 280104.65 – Пожарная безопасность для выполнения контрольной работы № 1 по высшей математике.
Одобрено на заседании Методического совета ГОУ ВПО «УРАЛЬСКИЙ ИНСТИТУТ ГОСУДАРСТВЕННОЙ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ».
Протокол № 4 от 15 ноября 2007г.
© Худякова С.А., 2007 © Бараховская О.В., 2007
© УрИ ГПС МЧС России, 2007
Содержание
Вступление. 4 Литература. 5 Выполнение и оформление контрольных работ. 5 Варианты контрольной работы.. 6 Указания к выполнению контрольной работы 1. 7 Тема 1. Элементы линейной алгебры и аналитической геометрии. 7 Примеры решения типовых задач. 8 Тема 2. Введение в математический анализ 19 Примеры решения типовых задач. 20 Тема 3. Дифференциальное исчисление функции одной переменной. 25 Примеры решения типовых задач. 26 Задания контрольной работы № 1. 27 Основные формулы.. 43
Вступление
Данные методические рекомендации составлены в соответствии с рабочей программой по дисциплине высшая математика и предназначены для слушателей I курса факультета заочного обучения по специальности 280104.65 – Пожарная безопасность. Они содержат краткие теоретические сведения по основным разделам курса и подробное решение типовых задач для самостоятельной подготовки к выполнению контрольной работы № 1. В процессе изучения дисциплины высшая математика слушатели 1 курса факультета заочного обучения по специальности 280104.65 – Пожарная безопасность должны: знать:
– основные понятия и методы высшей алгебры, аналитической геометрии; – основные понятия и методы математического анализа, дифференциального и интегрального исчисления, теории функций и функционального анализа; уметь:
– употреблять математическую символику при решении инженерных задач; – решать основные задачи общей алгебры и геометрии, дискретной математики; – решать основные задачи математического анализа; иметь представление:
– об арифметическом векторном пространстве (пространство R); – о линейном пространстве, его размерности. Все вышеперечисленные знания, умения и навыки приобретаются слушателями в процессе самостоятельной работы и на обязательных аудиторных занятиях.
Контрольная работа № 1 включает в себя практические задания по темам:
1. Элементы линейной алгебры и аналитической геометрии; 2. Введение в математический анализ; 3. Дифференциальное исчисление функции одной переменной. Литература 1. Шипачев В.С. Высшая математика: Учеб. для вузов / В.С. Шипачев. – 6-е изд., стер. – М.: Высш. шк., 2003. – 479 с. 2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. для втузов. В 2-х т. Т. I: – М.: Интеграл – Пресс, 2004. – 416 с. 3. Шипачев В.С. Задачник по высшей математике: Учеб. пособие для вузов / В.С. Шипачев. – 3-е изд., стер. – М.: Высш. шк., 2003. – 304 с. 4. Баврин И.И. Высшая математика: Учеб. для студ. естественнонаучных специальностей педагогических вузов. – 2-е изд., стер. – М.: Изд. центр «Академия»; Высш. шк., 2001. – 616 с. 5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. I: Учеб. пособие для втузов. – 5-е изд., испр. – М.: Высш. шк., 1999. – 304 с. 6. Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. – М.: Айрис-пресс, 2004. 7. Лунгу К.Н., Письменный Д.Т. Сборник задач по высшей математике. 1 курс. – М.: Айрис-пресс, 2004.
Выполнение и оформление контрольных работ
1. Слушатели выполняют контрольную работу в соответствии с учебным планом в сроки, установленные факультетом заочного обучения. 2. Слушатели должны выполнить один из 100 вариантов, номер, которого определяется по двум последним цифрам номера зачетной книжки. 3. Каждая контрольная работа выполняется в отдельной тетради в клеточку, ручкой любого цвета, кроме зеленого и красного, аккуратно и разборчивым почерком, чертежи выполняются простым карандашом с использованием инструмента. 4. На титульном листе следует указать фамилию, имя, отчество, должность и звание слушателя, его адрес с указанием почтового индекса, номер зачетной книжки, номер варианта. 5. Задания в контрольных работах выполняются по порядку, согласно расположению их в варианте. 6. На заключительном листе контрольных работ следует указать список литературы, которым Вы пользовались при их выполнении. 7. Если контрольные работы выполнены с нарушением всех вышеперечисленных указаний или не полностью, то они возвращаются слушателю для доработки без проверки. 8. Если работы не зачтены, внимательно изучите все замечания рецензента. Переделайте работы в соответствии с рекомендациями рецензента. 9. Переделанные работы предоставляются на проверку вместе с незачтенными работами. Варианты контрольной работы
Векторы Литература. [1], Гл. III, § 1-4, Гл. IX, § 1-5.; [3], Гл. III, § 1-4 задачи 1-5, 16-18, 22-24, 38-40, 42-47; Гл. X, § 1-3 задачи 6-14, 22-33. Можно использовать также [6], Гл. II, § 5.; [7], Гл. III, § 1 задачи 3.1.1., 3.1.13.-3.1.20. Линии второго порядка Литература. [1], Гл. III, § 7-8, Гл. IX, § 9-14.; [3], Гл. III, § 8 задачи 126-132, 139-147, 150-155.; Гл. X, § 10 задачи 166-171. Можно использовать также [6], Гл. III, § 11.; [7], Гл. IV, § 3 задачи 4.3.1., 4.3.28., 4.3.31., 4.3.60., 4.3.64., 4.3.105, 4.3.106. Примеры решения типовых задач № 1. Даны координаты вершин пирамиды А1 А2 А3 А4. А1 (0; 2; - 2), А2 (1; 0; - 1), А3 (0; 5; - 1), А4 (0; 2; 1). Найти: 1) длину ребра А1 А2; 2) угол между ребрами А1 А2 и А1 А4; 3) угол между ребром А1 А4 и гранью А1 А2 А3; 4) площадь грани А1 А2 А3; 5) объем пирамиды; 6) уравнение прямой А1 А2; 7) уравнение плоскости А1 А2 А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж. Решение 1. Найти длину ребра А1 А2.
2. Найти угол между ребрами А1 А2 и А1 А4.
где
3. Найти угол между ребром А1 А4 и гранью А1 А2 А3. Угол между ребром А1 А4 и гранью А1 А2 А3 вычисляется по формуле: Составим уравнение плоскости (А1 А2 А3). Воспользуемся уравнением плоскости, проходящей через три заданные точки А1 (0; 2; -2), А2 (1; 01; -1) и А3 (0; 5; -1) имеет вид:
отсюда 4. Найти площадь грани А1 А2 А3. Найдем векторное произведение векторов S параллелограмма
Площадь треугольника равна половине площади параллелограмма, т.е. S треугольника = 5. Найти объем пирамиды А1 А2 А3 А4. Объем пирамиды равен одной шестой модуля смешанного произведения трех векторов, т.е.
6. Составить уравнение прямой А1 А2.
7. Составить уравнение плоскости А1 А2 А3.
(Решение см. в пункте 3). 8. Составить уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3.
z
0 y А2 А3 x А1
№ 2. а) Дан треугольник АВС с вершинами А (-5; 4), В (3; -2), С (-8; -5). Составить уравнение медианы СК и высоты АН.
Решение 1) А (х - х0) + В (у – у0) = 0, где (А; В) координаты нормального вектора прямой СК, (х0; у0) – координаты точки С (-8; -5). Найдем координаты точки К.
6(х + 8)- 7(у + 5) = 0 6 х - 7 у + 13 = 0 - уравнение медианы СК.
2) А (х - х0) + В (у – у0) = 0, где (А; В) координаты нормального вектора прямой АН, (х0; у0) – координаты точки А (-5; 4). Нормальным вектором прямой АН является вектор 11(х + 5)+ 3(у - 4) = 0 11 х + 3 у + 43 = 0 - уравнение высоты АН.
А (-5; 4)
К
х В (3; -2)
Н С (-8; -5).
б) Даны две последовательные вершины параллелограмма А (- 5; 3) и В (2; 7), точка пересечения его диагоналей К (- 1; 2). Найти остальные вершины параллелограмма.
Решение 7 В
А 3 К С х - 5 - 4 - 1 3
Д - 3
Для нахождения координат точки С воспользуемся формулами деления отрезка в данном отношении:
Для нахождения координат точки Д воспользуемся формулами деления отрезка в данном отношении:
№ 3. Установить, какая линия определяется данным уравнением. Изобразить данную линию на чертеже, охарактеризовав ее. а) х 2 + у 2 + 6 х +10 у – 15 = 0. Преобразуем данное уравнение: х 2 + 6 х + 9 + у 2 + 10 у – 9 – 25 - 15 = 0;
(х +3)2 + (у + 5)2 - 49 = 0 – уравнение окружности с центром в точке (- 3; - 5), радиусом 7.
х
О (- 3; - 5)
б) 9 х 2 + 16 у 2 = 144. Разделим обе части уравнения на 144:
Координаты вершин эллипса: А 1,2 ( А 1,2 ( Большая ось эллипса | А 1 А 2| = 2 а = 8, малая ось эллипса | В 1 В 2| = 2 b = 6. Определим координаты фокусов (фокусы эллипса находятся на большой оси), для этого воспользуемся формулой с 2 = а 2 - b 2;
Координаты фокусов: F 1,2 ( F 1,2 (
Построим график эллипса у В 1 3
А 2 F 2 F 1 А 1
- 4 -
- 3 В 2 в) 25 х 2 - 9 у 2 - 100 х – 54 у – 206 = 0. Преобразуем данное уравнение:
(25 х 2 - 100 х)– (9 у 2 + 54 у) – 206 = 0; 25(х 2 - 4 х)– 9(у 2 + 6 у) – 206 = 0; 25(х 2 - 4 х + 4)– 100 – 9(у 2 + 6 у + 9) + 81 –206 = 0; 25(х – 2)2 – 100 – 9(у + 3)2 + 81 – 206 = 0; 25(х – 2)2 – 9(у + 3)2 – 225 = 0; 25(х – 2)2 – 9(у + 3)2 = 225;
а 2 = 9, b 2 = 25, значит, а = 3, b = 5. Центр гиперболы находится в точке (2; - 3) Координаты вершин гиперболы: действительные вершины: А 1 (5; - 3), А 2 (- 1; - 3), мнимые вершины: В 1 (2; 2), В 2 (2; - 8). Действительная ось гиперболы | А 1 А 2| = 2 а = 6, мнимая ось гиперболы | В 1 В 2| = 2 b = 10. Определим координаты фокусов (фокусы гиперболы находятся на действительной оси), для этого воспользуемся формулой с 2 = а 2 + b 2;
Координаты фокусов: F 1 (5 +
Построим график гиперболы В 1
- 3 - 1 2 х F 2 А 2 А 1 F 1
- 8 В 2 г) х = 1 - Преобразуем данное уравнение: х - 1 = - (х – 1)2 = (-
Построим график параболы:
№ 4. Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса и методом Крамера. Метод Крамера.
1. Найдем определитель данной системы: 2. Найдем определители
3. Находим значения неизвестных
4. Делаем проверку:
Ответ: Метод Гаусса. Составим матрицу из коэффициентов перед неизвестными переменными и свободных членов.
Приведем матрицу к треугольному виду. Поменяем в матрице первую и вторую строки, для того, чтобы на первом месте была единица.
зафиксируем первую строку, домножим ее на «-2», суммируя результат со второй строкой; результат записать на место второй строки; домножим ее на «-3», суммируя результат с третьей строкой; результат записать на место третьей. ~
~ ~
Ответ:
№ 5. Найти обратную матрицу, выполнить проверку: Пусть дана матрица 1) Вычисляем определитель матрицы А: 2) Находим алгебраические дополнения элементов этого определителя:
3) Записываем обратную матрицу:
4) Выполнить проверку:
= = Ответ:
Тема 2. Введение в математический анализ Непрерывность функции Литература. [2], Гл. II, § 10; [3], Гл. IV, § 1-3 задачи 224-233. Можно использовать также[6], Гл. V, § 19.; [7], Гл. VI, § 5 задачи 6.5.4., 6.5.6., 6.5.11.
Примеры решения типовых задач № 6. Вычислить: 1. Примеры и решение пределов с использованием теорем о пределах: · ·
2. Примеры и решение пределов с использованием методов раскрытия неопределенностей, а также теорем о пределах: · = Для того, чтобы раскрыть неопределенность вида = · Здесь мы также имеем неопределенность вида = = = · Здесь мы также имеем неопределенность вида = = =
3. Вычислить. · Для того, чтобы раскрыть неопределенность вида = Осталось воспользоваться теоремами о пределах, а также тем, что функции =
· Для того, чтобы раскрыть неопределенность вида = Осталось воспользоваться теоремами о пределах, а также тем, что функции =
· Для того, чтобы раскрыть неопределенность вида = Осталось воспользоваться теоремами о пределах, а также тем, что функции =
4. Примеры и решение пределов с помощью замечательных пределов: · Домножим числитель и знаменатель дроби на «3» и получим: = Используя теоремы о пределах и первый замечательный предел, получаем: = 3 · Поделим числитель и знаменатель дроби под знаком предела на х, после чего воспользуемся предыдущим примером, получим: = · Сведем данный предел к первому замечательному пределу, для этого сделаем замену у = х - = В числителе дроби используем формулу приведения, тогда = · В данном случае неопределенность вида | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


 (ед)
(ед) , отсюда
, отсюда ,
, и
и  .
. и
и  ,
,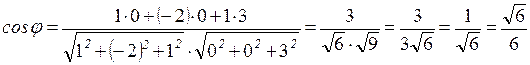 , значит
, значит 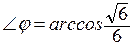 .
. , где
, где  - нормальный вектор плоскости (А1 А2 А3).
- нормальный вектор плоскости (А1 А2 А3). 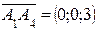 .
.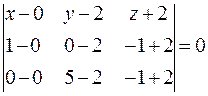 ;
; 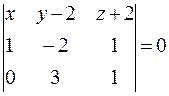 ;
; ;
; ;
;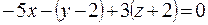 ;
; (умножим на - 1);
(умножим на - 1);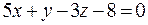 - уравнение плоскости А1 А2 А3.
- уравнение плоскости А1 А2 А3.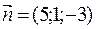 - нормальный вектор плоскости А1 А2 А3.
- нормальный вектор плоскости А1 А2 А3. ,
, .
.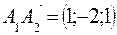 и
и 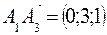 .
. ,
, 


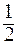
 (ед 2).
(ед 2). ,
, .
.
 - направляющий вектор прямой
- направляющий вектор прямой 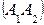 , точка
, точка  лежит на прямой. Тогда каноническое уравнение прямой
лежит на прямой. Тогда каноническое уравнение прямой  имеет вид:
имеет вид:  ,
, 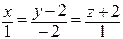 .
. - уравнение плоскости А1 А2 А3.
- уравнение плоскости А1 А2 А3.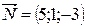 - нормаль плоскости А1 А2 А3. Высота опущенная из вершины А4 (0; 2; 1) на грань А1 А2 А3 перпендикулярна к ней.
- нормаль плоскости А1 А2 А3. Высота опущенная из вершины А4 (0; 2; 1) на грань А1 А2 А3 перпендикулярна к ней.
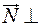 (А1 А2 А3) и высота А4H
(А1 А2 А3) и высота А4H  (А1 А2 А3), следовательно
(А1 А2 А3), следовательно 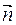 ||(А4H). Вектор
||(А4H). Вектор  является направляющим вектором высоты А4H. Тогда каноническое уравнение прямой
является направляющим вектором высоты А4H. Тогда каноническое уравнение прямой  имеет вид:
имеет вид: 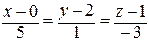 ,
,  .
. А4
А4

 ;
; 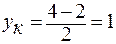 ; К (-1;1);
; К (-1;1);  = (7; 6); нормальный вектор прямой СК имеет координаты (6; -7).
= (7; 6); нормальный вектор прямой СК имеет координаты (6; -7).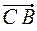 = (11; 3).
= (11; 3). у
у
 ,
, 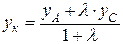 , где
, где  - отношение
- отношение  ,
,  и
и  .
. ,
,  . С (3; 1).
. С (3; 1). ,
,  , где
, где  ,
, 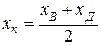 и
и  .
. ,
,  . Д (- 4; - 3).
. Д (- 4; - 3).

 у
у (каноническое уравнение эллипса
(каноническое уравнение эллипса  ), а 2 = 16, b 2 = 9, значит, а = 4, b = 3.
), а 2 = 16, b 2 = 9, значит, а = 4, b = 3. а; 0), В 1,2 (0;
а; 0), В 1,2 (0;  .
.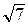 ; 0).
; 0). Эксцентриситет эллипса
Эксцентриситет эллипса  (для случая b > а,
(для случая b > а,  ).
).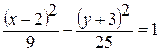 – каноническое уравнение гиперболы со смещенным центром
– каноническое уравнение гиперболы со смещенным центром 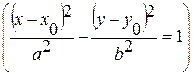 .
. .
. ; - 3), F 2 (2 -
; - 3), F 2 (2 -  Эксцентриситет эллипса
Эксцентриситет эллипса 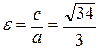 (для случая
(для случая 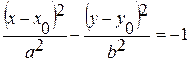 ,
,  .
. ;
;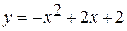 - общее уравнение параболы, с вершиной в точке (1; 3), направлением ветвей вниз, с осью симметрии х = 1.
- общее уравнение параболы, с вершиной в точке (1; 3), направлением ветвей вниз, с осью симметрии х = 1.


 ;
; .
. , где
, где  получен из
получен из 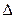 путём замены первого столбца на столбец свободных членов, остальные определители находятся аналогично.
путём замены первого столбца на столбец свободных членов, остальные определители находятся аналогично.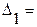
 ,
, 
 ,
, 
 .
. :
: 
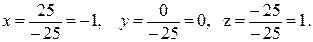
 ;
;  ;
;  .
.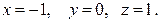

 ~
~ ~ поменяем вторую и третью строки местами
~ поменяем вторую и третью строки местами ~ разделим вторую строку на 3, а третью на «-5»
~ разделим вторую строку на 3, а третью на «-5»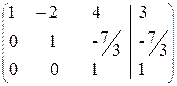 получаем систему
получаем систему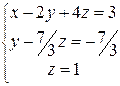 ,
, 
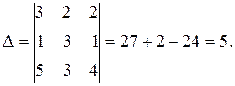


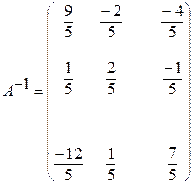
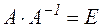 .
.

 =
= =
= =
= 
 (1+
(1+  ) = 1 + 0 = 1;
) = 1 + 0 = 1;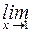 (4x3 - х + 2) =
(4x3 - х + 2) = 
 = [
= [  = 0,
= 0,  ) = 0] =
) = 0] = =
= =
=  =
=  = - 9.
= - 9.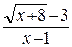 =
= =
= 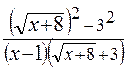 =
= =
=  =
=  =
= .
.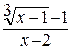 =
=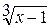 и 1, чтобы получить разность кубов в числителе:
и 1, чтобы получить разность кубов в числителе: =
=  =
= =
=  =
= =
=  =
=  .
.
 =
=  =
= =
=  =
= ,
,  и
и 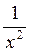 - бесконечно малые при х
- бесконечно малые при х  .
. =
=  .
. =
=  =
=  =
= ,
, 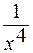 и
и  - бесконечно малые при х
- бесконечно малые при х  =
=  .
. =
=  =
=  =
= и
и  =
=  .
.
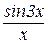 =
=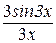 =
= =3.
=3. =
=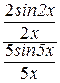 =
=  .
.
 =
= . Тогда
. Тогда 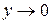 при х
при х 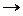

 =
= =
= 
 =
=  =
= , для ее раскрытия сделаем замену у =
, для ее раскрытия сделаем замену у =  . Тогда
. Тогда 


