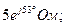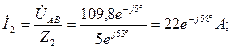Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет однофазных цепей переменного токаСодержание книги
Поиск на нашем сайте
Расчет цепей переменного тока целесообразно осуществлять, используя комплексные числа. Для этого необходимо уметь выполнять действия с комплексными числами. Ниже даются основные сведения по действиям с комплексными числами. Известно, что любую величину, изменяющуюся по закону sin ωt, можно представить в виде вектора, вращающегося на плоскости с угловой частотой ω. А вектор на плоскости может быть описан в мнимой и действительной осях комплексным числом (рис. 1):
а – действительная часть; в – мнимая часть;
- модуль вектора (комплексного числа);
- его фаза. При определении фазы комплексного числа по приведенной формуле необходимо обращать внимание на знаки его действительной и мнимой части. Если и действительная и мнимая части отрицательны, то к значению полученного угла надо прибавить или вычесть из него 180, чтобы получить фактическое значение фазы. Если же действительная часть отрицательна, а мнимая положительна, то для получения фактического значения фазы следует поступать, как в предыдущем случае. При других значениях действительной и мнимой частей мы получаем фактическое значение фазы комплексного числа. Выше приведена алгебраическая форма комплексного числа. Комплексное число может быть представлено в тригонометрической форме
и в показательной форме
Д е й с т в и я с к о м п л е к с н ы м и ч и с л а м и Действия с комплексными числами рассмотрим на конкретных примерах. Пусть имеем два комплексных числа:
1). С л о ж е н и е к о м п л е к с н ы х ч и с е л:
2). В ы ч и т а н и е к о м п л е к с н ы х ч и с е л:
3). У м н о ж е н и е к о м п л е к с н ы х ч и с е л:
Умножение комплексных чисел удобно выполнять при представлении их в показательной форме. Так как
4). Д е л е н и е к о м п л е к с н ы х ч и с е л:
где
или
расхождение значения фазы на 0,1о получено за счет округления. Активная и реактивная мощность определяется произведением комплекса напряжения на сопряженный комплекс тока:
где Р – активная мощность, а Q – реактивная мощность. Полная мощность
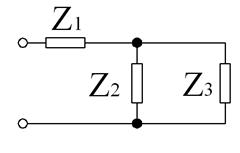
где U и I - модули комплексов напряжения и тока. Усвоив действия с комплексными числами, можно приступить к выполнению задания № 2, условия по которому даны ниже. Три потребителя, параметры которых заданы в таблице №2, включены в цепь однофазного переменного тока напряжением 220 В. Схема включения показана на рис. 2а и 2б. Требуется: 1. Определить полное сопротивление каждого потребителя и всей цепи. 2. Определить потребляемый ток, активную, реактивную и полную мощность, угол сдвига по фазе между током и напряжением. 3. Построить векторную диаграмму.
a) б) Рис. 2. Схема включения потребителей: а) для нечетного варианта; б) для четного варианта.
Таблица 2
Пример 2. Два потребителя с параметрами r2 = 3 Ом; xL2 = 4 Ом; r3 = 8 Ом; xС3 = 8 Ом соединены параллельно друг другу. Последовательно с ними включен потребитель с параметрами r1= 4 Ом; xL1= 8 Ом; xС1= 5 Ом. Найти полное сопротивление потребителей и всей цепи, потребляемый ток, активную, реактивную и полную мощность, угол сдвига по фазе между током и напряжением, если напряжение в сети 220 В. Р е ш е н и е: Схема включения потребителя показана на рисунке 2а. Находим полное сопротивление потребителей
Z1= r1+ jxL1- jхС1=4+ j8- j5= 4+ j3= ׀Z1׀ = φ = arctg хL1 / r1 = arctg 3/4 = 370; Z2 = r2 + jx L2 = 3 + j4 = ׀Z2׀ = φ = arctg хL2 / r2 = arctg 4 / 3 = 530; Z3 = r 3 – jx C3 = 8 - j8 = ׀Z3׀ = φ = arctg (-8/8) = - 450. Сопротивление между узлами А В
= Полное сопротивление цепи Z = Z1 + ZAB = 4 + j3 + 4,3 + j2,3 = 8,3 + j5,3 = Считая начальную фазу напряжения равной нулю, находим общий ток
Находим напряжение между узлами А В и токи в ветвях
Мощность, потребляемая цепью: -активная P = I2·r = I·U·cos φ = 22,4 · 220 · cos (-330) = 4133 Вт; -полная S = I·U = 22,4 · 220 = 4928 ВА; -реактивная Q = I·U· sin φ = 22,4 · 220 · sin(- 330) = 2684 ВАр; φ = - 330. Находим падение напряжения на Z1 Для построения векторной диаграммы определяем масштаб построения величины тока и напряжения: mI = 2 A/cм; mU = 20 B/cм.
Векторная диаграмма
Задание № 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.170 (0.008 с.) |


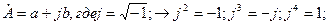 где
где






 .
. ;
;  ;
; ;
;  ;
; 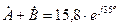 .
. ;
;  ;
; ;
;  ;
; 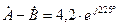 .
. ;
; ;
;  ;
; 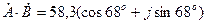 ;
; .
.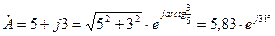 и
и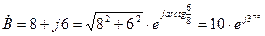 , то
, то 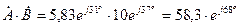 .
. ;
; -сопряженный комплекс, отличающийся от комплекса
-сопряженный комплекс, отличающийся от комплекса  знаком фазы, если комплекс представлен в показательной форме или знаком мнимой части, если комплекс представлен в алгебраической или тригонометрической форме.
знаком фазы, если комплекс представлен в показательной форме или знаком мнимой части, если комплекс представлен в алгебраической или тригонометрической форме. ;
;  ;
; ;
; 
 ;
; ,
, ,
,

 Ом;
Ом;