
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1 элементы линейной алгебрыСодержание книги
Поиск на нашем сайте СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Цель курса математики в системе подготовки экономиста– освоение необходимого математического аппарата. Это необходимо для анализа моделирования и решения прикладных экономических задач, в том числе с использованием ЭВМ. Задачи изучения математики как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке умения моделировать реальные технические процессы.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
Дисциплина «Математика» предназначена для реализации федерального стандарта к минимуму содержания и уровню подготовки выпускников по направлению: 21.03.02 «Землеустройство и кадастры» - является единой для всех форм обучения. 1 Цель и задачи дисциплины Изучение дисциплины «Математика» имеет целью дать студентам основы теоретических и методологических знаний и практических навыков: - по фундаментальной математике; - решению и исследованию математических задач, применению вычислительной техники для решения. Целью изучения дисциплины «Математика» состоит в том, что на основе математических понятий и методов продемонстрировать студентам сущность и возможности применения математического аппарата к решению практических задач принятия управленческих решений, научить приемам исследования и решения математически формализованных задач, выработать умение анализировать и оценивать полученные результаты. 2 Входные требования и место дисциплины в структуре ООП бакалавриата Дисциплина «Математика» относится к базовой части математического и естественнонаучного цикла. Освоение дисциплины «Математика» опирается на знания, полученные в школьном курсе математики и информатики. Начальные разделы этой дисциплины являются предшествующими для следующих дисциплин: «Экономико-математические методы и моделирование», «Метрология, стандартизация, сертификация». 3 Требования к результатам освоения дисциплины «Математика» Необходимыми требованиями к знаниям и умениям, приобретаемым при изучении курса, являются: формирование у студентов четких знаний по данной дисциплине, умения ориентироваться в определениях и свойствах в зависимости от поставленной задачи, способности использовать полученные навыки при изучении профильных дисциплин. Процесс изучения дисциплины направлен на формирование следующих компетенций, представленных в таблице. Таблица - Структура компетенций, формируемых в результате изучения дисциплины
Тема 3 Векторы
Векторы на плоскости и в пространстве (сложение, вычитание, умножение на число). Координаты и длина вектора, п-мерный вектор. Линейная комбинация, линейная зависимость и независимость векторов. Понятие о векторном (линейном) пространстве и его базисе. Собственные векторы и собственные значения матрицы. Характеристический многочлен матрицы. (1, гл. 3, § 3.1 – 3.3, 3.7; с. 63 – 66, 68 – 72, 82 – 84); (2, гл. 3). Необходимо рассмотреть и усвоить понятие вектора, обозначения векторов, определение длины векторов, определение коллинеарных векторов, противоположных векторов. Изучить операции сложения и вычитания векторов на плоскости и в пространстве. Правило параллелограмма, многоугольника, параллелепипеда. Надо уяснить, что скалярное произведение векторов это произведение модулей их длин на косинус угла между ними, а скалярное произведение в координатах равно сумме произведений соответствующих координат. Разобрать задачи с решениями (1,3.14–3.17). Необходимо разобраться с понятием n-мерного вектора и векторного пространства, изучить свойства векторного пространства. Множества всех плоских и пространственных векторов, для которых определены операции сложения и умножения, а также умножения вектора на число, являются простейшими примерами векторных пространств. В данной теме обобщается понятие вектора и дается определение векторного пространства. Необходимо уяснить понятие линейной комбинации, линейной зависимости и линейной независимости векторов, а именно: линейная комбинация векторов a1,a2,…,an векторного пространства R равна сумме произведений этих векторов на произвольные действительные числа (am=l1a1+l2a2+…+lm-1am-1). Линейно зависимые векторы (как и строки матрицы) - это такие векторы, для которых существуют такие числа l1,l2,…,lm не равные нулю одновременно такие, что l1a1+l2a2+…+lmam=0. Линейно независимые - это вектора, для которых l1a1+l2a2+…+lmam=0 возможно только при одновременном равенстве нулю всех чисел l1=l2=…=lm=0. В случае линейной зависимости векторов, по крайней мере, один из них выражается через остальные. Необходимо уяснить, что любой вектор пространства может быть представлен в виде линейной комбинации векторов базиса. Особую роль в приложениях математики играют векторы, обладающие следующим свойством: при умножении квадратных матриц на них образуются новые векторы, коллинеарные исходным. Такие векторы получили название собственных векторов матрицы, а соответствующие им числа – собственных значений матрицы. Точное определение собственных векторов и значений приведено в (1, с. 82). Рекомендуется разобрать задачи с решениями N 3.2, 3.3, 3.7 и задачи для самостоятельной работы N 3.18 – 3.20, 3.27, 3.28 по учебнику (1) и аналогичные задачи по практикуму (2). РАЗДЕЛ II ВВЕДЕНИЕ В АНАЛИЗ Тема 4 Функции Понятие о множествах. Действительные числа и числовые множества. Постоянные и переменные величины. Функции и способы их задания. Область определения функции. Четные, нечетные, монотонные и ограниченные функции. Сложная функция. Понятие элементарной функции. Основные элементарные функции и их графики. Неявные функции. (гл. 4, § 4.1 – 4.3, 4.6; с. 95 – 99, 100 – 103,.115 – 117); (2, гл. 5,4). Прежде всего, полезно ознакомиться с некоторыми логическими символами и кванторами, чтобы использовать их в дальнейшем для сокращения записей (1, с. 123). Изучение темы следует начать с основных понятий теории множеств, [1, с. 123 – 124]. Далее нужно четко усвоить важнейшее понятие математического анализа – функции, уметь находить область ее определения, знать три способа задания функции: аналитический, графический, табличный. Студенту нужно знать простейшие преобразования для построения функций, как-то: сдвиг графика y=f(x+a)+b вправо при а < 0 и влево при a > 0, а также на В курсе рассматриваются в основном элементарные функции. Студент должен уяснить определение элементарной функции (1, с. 132) четко знать свойства и строить графики следующих основных элементарных функций: у=С (постоянная), у=xn (степенная), у=ax (показательная), у=logax (логарифмическая). Необходимо усвоить понятие сложной функции (функции от функции). Построение графика четной (нечетной) функции можно значительно упростить, если учесть, что графики четных функций симметричны относительно оси Оу, а нечетных – относительно начала координат. Одним из характерных свойств функции является монотонность (т.е. возрастание или убывание на каком-либо промежутке). Студенту необходимо уяснить, что функции находит широкое применение в экономической теории. Знать конкретные виды функций и их сущность (функция полезности, функция издержек и т.д.). Уравнение линии на плоскости. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой. Уравнение прямой, проходящей через данную точку в заданном направлении, через две данные точки. Условия параллельности и перпендикулярности двух прямых. Точка пересечения двух прямых. (1, гл. 5, § 5.1–5.5, 5.7, с. 123–132, 138, 139). Студенту необходимо прочно усвоить материал, который будет использован при изучении экономико-математических методов и прикладных моделей (линейное программирование). Большое значение здесь имеет определение уравнения линии на плоскости как уравнения с двумя переменными х и у, которому удовлетворяют координаты каждой точки этой линии и не удовлетворяют координаты любой точки, не лежащей на ней. Из этого определения следуют два важных для практики положения, которые нужно знать: 1. Если задано уравнение линии, то можно установить, принадлежит ли ей какая-либо точка плоскости. Для этого достаточно подставить координаты точки в уравнение линии вместо переменных х и у. Если окажется, что они удовлетворяют уравнению, то точка принадлежит линии, в противном случае – не принадлежит. 2. Координаты точки пересечения двух линий, заданных своими уравнениями, удовлетворяют обоим уравнениям. Поэтому для нахождения координат точки пересечения двух линий нужно решить систему, составленную из их уравнений. Этот вопрос должен быть усвоен твердо. Студент должен знать простейшие виды уравнений прямой и уметь пользоваться ими при решении задач. Соответствующий учебный материал приведен в (1, с.95–99, 100–103,115–116). Обратите особое внимание на нахождение уравнений прямых, параллельной и перпендикулярной данной прямой (пример 4.5). Рекомендуется разобрать задачи с решениями N4.1–4.3, 4.5, 4.10, 4.12 и задачи для самостоятельного решения N 4.14–4.19, 4.21–4.23 по учебнику (1) и аналогичные задачи по практикуму (2). Тема 6 Производная Задачи, приводящие к понятию производной. Производная, ее геометрический, механический и экономический смысл. Уравнение касательной к плоской кривой; Дифференцируемость функции. Связь между дифференцируемостью и непрерывностью функции (необходимый признак дифференцируемости). Основные правила и основные формулы дифференцирования. Производная сложной функции Производные высших порядков. (1, гл. 7, § 7.1 – 7.7, с. 176 – 205); (2, гл. 7). Необходимо изучить задачи, приводящие к понятию производной: задачи о касательной и задачи о скорости движения (1, с.176, 177), задачи о производительности труда (экономический смысл производной). После этого нужно усвоить определение производной как предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю. Нужно знать обозначение производной, алгоритм ее вычисления, основываясь на теории пределов. Студент обязан понимать геометрический и механический смысл производной (1,с.178, 181), уметь решать простейшие задачи по вычислению производной на основе алгоритма ее вычисления; знать и уметь применять основные правила дифференцирования, вычислять производную сложной и обратной функций. При этом нужно знать четко правила вычисления элементарных функций (1,с. 188,193), знать наизусть таблицу производных (1, с.192). Это позволит усвоить дифференцирование сложных функций, обратных функций, неявно заданных функций (1, с.193), находить производные от произведения, суммы, разности, а также вычислять производные высших порядков. Нужно знать использование понятия производной в экономике, понятие эластичности функции, свойства эластичности функции. Изучая материал этой темы, студенты знакомятся с необходимым условием дифференцируемости функции. Необходимо четко уяснить, что из дифференцируемости функции в некоторой точке следует ее непрерывность в этой точке. Обратная теорема несправедлива, так как существуют непрерывные функции, которые в некоторых точках могут не иметь производной (1, с. 179, 180). Рекомендуется разобрать задачи с решениями N 7.1–7.8, 7.10, 7.13, 1.15–7.17 и задачи для самостоятельной работы N 7.20–7.29, 7.35, 7 42, 7.43, 7.46–7. 49 по учебнику (1) и аналогичные задачи по практикуму (2). Для усвоения темы нужно решить задачи контрольной работы, ответить письменно на теоретические вопросы в контрольной работе. ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ ВАРИАНТ №1
ВАРИАНТ №2
ВАРИАНТ №3
ВАРИАНТ №4
ВАРИАНТ №5
ВАРИАНТ №6
ВАРИАНТ №7
ВАРИАНТ №8
ВАРИАНТ №9
ВАРИАНТ №10
ВОПРОСЫ К ЭКЗАМЕНУ 1. Основные понятия о матрицах. 2. Операции над матрицами. 3. Определители квадратных матриц. 4. Свойства определителей. 5. Обратная матрица. 6. Ранг матрицы. 7. Основные понятия системы линейных уравнений. 8. Метод обратной матрицы. 9. Метод Крамера. 10. Метод Гаусса. 11. Уравнение линии на плоскости. 12. Уравнение прямой. 13. Условия параллельности и перпендикулярности прямых. Расстояние от точки до прямой. 14. Понятие функции. Основные свойства функций. 15. Предел числовой последовательности. 16. Предел функции в бесконечности и в точке. 17. Бесконечно малые величины и их свойства. 18. Бесконечно большие величины. 19. Основные теоремы о пределах. 20. Замечательные пределы. 21. Непрерывность функции. 22. Определение производной. Основные правила дифференцирования. 23. Производная сложной функции. 24. Основные теоремы дифференциального исчисления. 25. Правило Лопиталя. 26. Возрастание и убывание функции. 27. Экстремум функции. 28. Наибольшее и наименьшее значение функции на отрезке. 29. Выпуклость функции. Точки перегиба. 30. Асимптоты графика функции. 31. Понятие дифференциала функции. 32. Частные производные первого порядка. 33. Частные производные высших порядков. 34. Экстремумы функций двух переменных. 35. Условный экстремум. 36. Метод наименьших квадратов.
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
1. Кремер, Н.Ш. Практикум по высшей математике для экономистов / / Н.Ш.Кремер – М.: ЮНИТИ-ДАНА, 2002. 2. Кремер, Н.Ш. Высшая математика для экономистов / Н.Ш.Кремер – М.: Банки и биржи, ЮНИТИ, 2009. Математический анализ и линейная алгебра. Учебное–методическое пособие. / Под ред. Н.Ш.Кремера - М.: ВЗФЭИ, 20 СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Цель курса математики в системе подготовки экономиста– освоение необходимого математического аппарата. Это необходимо для анализа моделирования и решения прикладных экономических задач, в том числе с использованием ЭВМ. Задачи изучения математики как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке умения моделировать реальные технические процессы.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
Дисциплина «Математика» предназначена для реализации федерального стандарта к минимуму содержания и уровню подготовки выпускников по направлению: 21.03.02 «Землеустройство и кадастры» - является единой для всех форм обучения. 1 Цель и задачи дисциплины Изучение дисциплины «Математика» имеет целью дать студентам основы теоретических и методологических знаний и практических навыков: - по фундаментальной математике; - решению и исследованию математических задач, применению вычислительной техники для решения. Целью изучения дисциплины «Математика» состоит в том, что на основе математических понятий и методов продемонстрировать студентам сущность и возможности применения математического аппарата к решению практических задач принятия управленческих решений, научить приемам исследования и решения математически формализованных задач, выработать умение анализировать и оценивать полученные результаты. 2 Входные требования и место дисциплины в структуре ООП бакалавриата Дисциплина «Математика» относится к базовой части математического и естественнонаучного цикла. Освоение дисциплины «Математика» опирается на знания, полученные в школьном курсе математики и информатики. Начальные разделы этой дисциплины являются предшествующими для следующих дисциплин: «Экономико-математические методы и моделирование», «Метрология, стандартизация, сертификация». 3 Требования к результатам освоения дисциплины «Математика» Необходимыми требованиями к знаниям и умениям, приобретаемым при изучении курса, являются: формирование у студентов четких знаний по данной дисциплине, умения ориентироваться в определениях и свойствах в зависимости от поставленной задачи, способности использовать полученные навыки при изучении профильных дисциплин. Процесс изучения дисциплины направлен на формирование следующих компетенций, представленных в таблице. Таблица - Структура компетенций, формируемых в результате изучения дисциплины
РАЗДЕЛ 1 ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

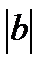 параллельно оси Ох вниз при b< 0 и вверх на
параллельно оси Ох вниз при b< 0 и вверх на 


