
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства непрерывных функцийСодержание книги
Поиск на нашем сайте
1. Напишите последовательность значений:
1)
2)
3)
4)
2. Пользуясь определением предела последовательности, докажите, что:
Докажите, что (Указание. Положить
3. Используя теоремы о пределах, найдите пределы:
4. Найдите односторонние пределы функции
5. Найдите точки разрыва функции
6. Пользуясь определением непрерывности функций, докажите, что функция
1) в точке
2) при
7. Найдите точки разрыва и исследуйте их характер для следующих функций:
1)
2)
3)
4) Тема 4. Замечательные пределы. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины
1. Найти пределы, используя первый замечательный предел:
2. Найти пределы, используя второй замечательный предел:
3. Используя таблицу эквивалентных бесконечно малых величин, найти пределы:
Тема 5. Дифференцирование функций 1. Воспользовавшись четырехступенчатым правилом дифференцирования, найдите производную функции
2. Найдите производные следующих функций, пользуясь формулами и правилами дифференцирования: 1)
4)
6)
9)
12)
15)
18)
3. Напишите уравнение касательной и нормали к параболе
4. Найдите мгновенную скорость движения тела в момент
Тема 6. Дифференцирование функций (продолжение)
1. Найдите производные следующих функций:
2. Найдите производные неявных функций:
3. Найдите производные
4. Найдите уравнения касательной и нормали к плоской линии
Тема 7. Дифференциал функции. Производные и дифференциалы высших порядков
1. Найдите дифференциал функции
2. Найдите дифференциал функции по формуле
3. Найдите приближенное значение
4. Найдите приближенное значение функций:
5. Найдите производные указанного порядка от заданных функций:
Тема 8. Аналитические приложения дифференцируемых функций
1. Определить интервал убывания и возрастания функций: 1) 3) 5) 7) 9) 2. Найти по правилу Лопиталя следующие пределы: 1) 3) 5) 7) 9) 11)
Тема 9. Экстремум функции
1. Исследуйте на экстремум следующие функции:
1) 3)
5)
2. Найдите точки перегиба функции и интервалы выпуклости (вогнутости) графиков следующих функций: 1) 3. Найдите асимптоты следующих функций:
1)
3)
4. Исследуйте функции и постройте их графики:
1)
3)
5)
7)
9)
Тема 10. Неопределенный интеграл. Основные свойства. Таблица неопределенных интегралов. Метод непосредственного интегрирования
1. Найдите неопределенные интегралы:
2. Применяя подходящие подстановки, найдите интегралы:
| ||
|
| Поделиться: |




 ;
;





 ;
;


 .
.









 где
где 


 – б.м.в.)
– б.м.в.)










 при
при 


 .
.

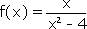



 непрерывна:
непрерывна:





 .
.







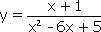
























 .
.




 ; 3)
; 3) 











 ;
;








 ;
;


 ; 10)
; 10) 

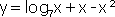
























 ; 19)
; 19) 






















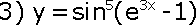








 ;
; 


























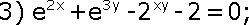






















































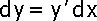

















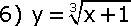





 ;
; 











































 ;
;









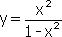












































 ;
;


 ; 6)
; 6) 



















































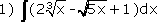
 ;
; 








 ;
;
































 ;
;










