
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение статистического распределения выборкиСодержание книги
Поиск на нашем сайте
Для построения эмпирического статистического распределения необходимо задать последовательность интервалов и соответствующих частот. Количество интервалов определяется по формуле Стреджесса: Длинна интервала находится по формуле:
Центр распределения определяется по формуле:
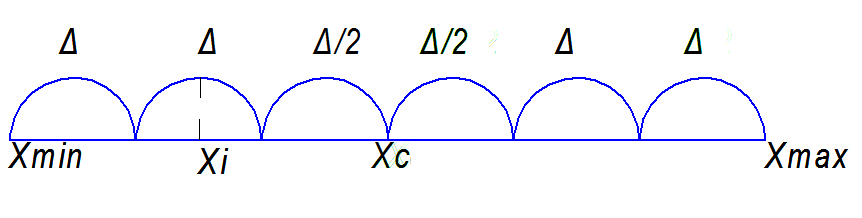
Границы элементарных интервалов определяются по схеме:
Проверка выдвинутой гипотезы о законе распределения исходных данных с доверительной вероятностью 0,95 по критерию Пирсона Используем для проверки критерий согласия Пирсона (критерий Для того чтобы проверить нулевую гипотезу

Найденное значение 1) Если 2) Если При этом существует вероятность № – номер интервала;
Исходя из того, что:
Гипотеза о том, что представленный закон распределения является нормальным, принимается. Идентификация законов распределения представлена на рисунке 18:

Гистограмма – инструмент, который позволяет наглядно изобразить и легко выявить структуру и характер изменения полученных данных (оценить распределение), которые трудно заметить при их табличном представлении. Важное преимущество гистограммы заключается в том, что она позволяет наглядно представить тенденции изменения измеряемых параметров качества объекта и зрительно оценить закон их распределения. Кроме того, гистограмма дает возможность быстро определить центр, разброс и форму распределения случайной величины. Строится гистограмма, как правило, для интервального изменения значений измеряемого параметра.

|
||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.109.147 (0.008 с.) |

 , где n – объем выборки;
, где n – объем выборки;

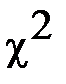 ).
).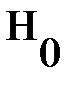 , необходимо вычислить теоретические частоты и наблюдаемое значение
, необходимо вычислить теоретические частоты и наблюдаемое значение 
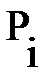 – теоретическая частота (вероятность) попадания в i-тый интервал.
– теоретическая частота (вероятность) попадания в i-тый интервал. сравниваем с расчетным значением
сравниваем с расчетным значением 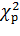
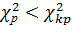 нет оснований отвергать гипотезу о распределении выборки по нормальному закону;
нет оснований отвергать гипотезу о распределении выборки по нормальному закону; , гипотеза отвергается.
, гипотеза отвергается. ошибочного принятия нулевой гипотезы, или ошибочного ее отвержения.
ошибочного принятия нулевой гипотезы, или ошибочного ее отвержения. – нижняя граница интервала;
– нижняя граница интервала; – верхняя граница интервала;
– верхняя граница интервала;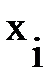 – середина i-го интервала;
– середина i-го интервала; – число значений попавших в i-ый интервала;
– число значений попавших в i-ый интервала; – теоретическая вероятность попадания в i-тый интервал;
– теоретическая вероятность попадания в i-тый интервал; – нормирующие случайные величины относительно найденного среднего;
– нормирующие случайные величины относительно найденного среднего; – функция Лапласа от нормирующего значения yi;
– функция Лапласа от нормирующего значения yi; =12,087.
=12,087. =0,639
=0,639



