Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 1. Выбор средства измерения для контроля параметров детали. Оценка вероятностных ошибок 1 и 2 рода при выполнении контроля.Содержание книги
Поиск на нашем сайте
Введение В данном курсовом проекте будут рассмотрены следующие вопросы: Выбор средства измерения и контроля параметров детали, оценка вероятностных ошибок первого и второго рода при выполнении контроля. Выбор средств измерения для контроля напряжения в заданных рабочих условиях. Определение поправок к показания прибора методом ситуационного моделирования. Оценка точности показаний. Оценка значений некоторой величины по результатам многократных ее измерений. Определение смущённости полученной оценки. Оценка необходимого количества измерений для достижения заданной точности.
Вопрос 1. Выбор средства измерения для контроля параметров детали. Оценка вероятностных ошибок 1 и 2 рода при выполнении контроля. Методика выбора средства измерения Характеристика производственных погрешностей Производственные погрешности - факторы, под непосредственным влиянием которых возникает погрешность. Виды производственных погрешностей: 1) Неточности станка - на погрешность обработки могут влиять: биение шпинделя, зазоры в сопряжениях деталей и узлов станка и т.п. 2) Неточности приспособления: - неточности элементов, устанавливающих обрабатываемую деталь; - неточности поверхностей корпуса, которыми приспособление устанавливается на станке; - неточности элементов, определяющих положение инструмента. 3) Неточности режущего инструмента - особенно существенны неточности мерного инструмента (зенкеры, развертки, метчики, протяжки и т.п.) и профильного (фасонные резцы, фрезы, шлифовальные круги и т.п.). от диаметра мерного инструмента непосредственно зависит диаметр обработанной поверхности, а от неточностей профильного – погрешности размеров обработанного профиля. 4) Неточности детали - деталь (полуфабрикат), поступающая на данную операцию, имеет погрешности обработки, возникшие при предшествующей операции. 5) Деформации станка, приспособления и инструмента – под влиянием сил резания в станке возникают упругие деформации. 6) Деформация детали - вызывается силами зажатия при ее закреплении и силами резания в процессе обработки. 7) Температурные деформации - разогревание станка. Нагревание детали в процессе обработки. 8) Деформации от внутренних напряжений- эти напряжения возникают в процессе изготовления заготовок и при механической обработке. При дальнейшей обработке и снятии слоев металла происходит перераспределение напряжений до нового их уравновешивания, вследствие чего форма обработанной поверхности и детали в целом может исказиться. 9) Неточности установки инструмента на размер(непосредственно влияют на величину размера) - заменяя затупившийся инструмент, нельзя придать ему точно такое же положение, какое занимал прежний. 10) Неточности измерения размера - эти неточности являются следствием неточностей измерительного инструмента или прибора и неточностей, сопутствующих процессу измерения (ошибки в настройке прибора, отсчете показаний инструмента и т.п.). [1]
Точность измерения Точность измерения - характеристика измерения, отражающая степень близости его результатов к истинному значению измеряемой величины. Чем меньше результат измерения отклоняется от истинного значения величины, то есть чем меньше его погрешность, тем выше точность измерения., независимо от того, является ли погрешность систематической, случайной или содержит ту и другую составляющие. Иногда в качестве количественной оценки точности измерения указывают погрешность, однако погрешность является понятием, противоположным точности, и логичнее в качестве оценки точности измерения указывать обратную величину относительной погрешности (без учёта её знака); например, если относительная погрешность равна ±10—5, то точность равна 105. Источники погрешности Погрешность обуславливается следующими причинами: 1) математическое описание задачи является не точным, в частности не точно заданы исходные данные описания; 2) применяемый для решения метод часто не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций; поэтому вместо точного решения задачи приходится прибегать к приближенному; 3) при вводе данных в машину, при выполнении арифметических операций и при выводе данных производятся округления. Погрешности, соответствующие этим причинам, называют: 1) неустранимой погрешностью; 2) погрешностью метода; 3) вычислительной погрешностью.
Многократные измерения Многократное измерение — измерение одного размера величины, результат этого измерения получают из нескольких последующих однократных измерений (отсчетов). Многократные измерения показывают, что результаты отдельных наблюдений отличаются друг от друга. Отличия наблюдаются также в результатах отдельных серий многократных измерений. В метрологии принято различать равноточные и неравноточные измерения. Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той лее методике при неизменных внешних условиях. При равноточных измерениях СКО результатов всех рядов измерений равны между собой. Если измерения выполнялись не в одинаковых условиях, то результаты нельзя считать одинаково надежными, такие измерения называют неравноточными. [3]
Грубые погрешности Грубые погрешности при измерениях – источник возможных серьезных ошибок в решениях, принимаемых при управлении технологическими процессами, контроле качества продукции и т.п. Грубые ошибки возникают при выходе из строя элементов измерительного канала, случайных помех в каналах передачи информации, из-за ошибок в проведении эксперимента, неправильного чтения показаний измерительного прибора, ошибок оператора при вводе исходных данных в компьютер и целого ряда других причин. Это приводит к тому, что нарушается одно из основных условий правомерности статистической обработки результатов измерений – требование однородности выборки, т.е. принадлежности результатов одной и той же генеральной совокупности. Очевидно, что совместно обрабатывать данные, принадлежащие различным генеральным совокупностям, не имеет смысла. Однако формально определить аномальные результаты не представляется возможным. Во-первых, по своим значениям они могут не отличаться существенно от значений интересующей генеральной совокупности. В этом случае их присутствие может быть обнаружено по виду смещающейся кривой плотности распределения. Наличие такого рода аномальных результатов называется загрязнением выборки. Выделить и удалить из анализируемой выборки подобные результаты практически невозможно. Во-вторых, результаты могут существенно отличаться по своим значениям от большинства других результатов выборки. Такие результаты называются промахами, и они могут быть исключены из рассматриваемой выборки. В-третьих, результаты могут не входить в компактную группу результатов измерений, но и не быть при этом существенно от них отличными. Такого рода результаты называют предполагаемыми промахами. Для их исключения (или сохранения в выборке) необходимо применение специальных статистических методов. Закон распределения Законом распределения случайной величины -это всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Наиболее часто встречающийся на практике закон распределения – это нормальный закон распределения. Главная особенность, выделяющая этот закон среди других, состоит в том, что он является предельным законом, которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно. Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать. Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток. Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х1, х2,..., хn с соответствующими им вероятностями р1, р2,..., рn:
Интервальная оценка Интервальная оценка – оценка представляемая интервалом значений, внутри которого с задаваемой исследователем вероятностью находится истинное значение оцениваемого параметра. Интервал в интервальной оценке называется доверительным интервалом, задаваемая исследователем вероятность называется доверительной. В практике статистических вычислений применяются стандартные значения доверительной вероятности: 0,95, 0,98 и 0,99 (95%, 98% и 99% соответственно). Интервальная оценка математического ожидания определяется следующим образом, если исходная выборка распределена по нормальному закону, то можно показать, что оценка математического ожидания в виде среднего имеет дисперсию:
Если при проведении измерительного эксперимента возможно малое число наблюдений или закон распределения неизвестен, то оценка математического ожидания и СКО математического ожидания принимаются равными вычисленным оценкам. При заданной доверительной вероятности можно установить величину доверительного интервала для
Список литературы 1) Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. Численные методы. 2) Ганевский Г.М., Гольдин И.И. Допуски, посадки и технические измерения в машиностроении. - М.: Высш. шк., 1998. -288с. 3) Сергеев А. Г. Метрология, стандартизация и сертификация -М.: Изд-во Юрайт; ИД Юрайт, 2011 4) http://tms.ystu.ru/gost/eskd/grafika/002-4.htm 5) Батищева О.М. Общая теория измерений. Электронное учебное пособие. – СамГТУ: Лаборатория компьютерных технологий и дистанционного обучения; Самара, 2003. 6) Батищева О.М. Практикум. – Самара: СамГТУ, 2008. – 87 с. 7) Взаимозаменяемость и точность – http://cherch.ru/osnovi_vzaimozamenyaemosti/vzaimozamenyaemost_i_tochnost.html Введение В данном курсовом проекте будут рассмотрены следующие вопросы: Выбор средства измерения и контроля параметров детали, оценка вероятностных ошибок первого и второго рода при выполнении контроля. Выбор средств измерения для контроля напряжения в заданных рабочих условиях. Определение поправок к показания прибора методом ситуационного моделирования. Оценка точности показаний. Оценка значений некоторой величины по результатам многократных ее измерений. Определение смущённости полученной оценки. Оценка необходимого количества измерений для достижения заданной точности.
Вопрос 1. Выбор средства измерения для контроля параметров детали. Оценка вероятностных ошибок 1 и 2 рода при выполнении контроля.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.167.85 (0.008 с.) |

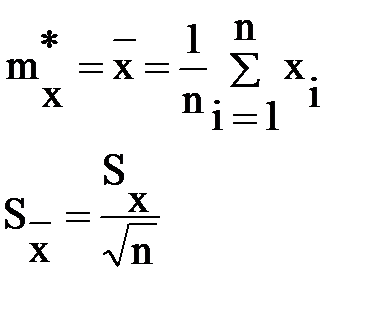
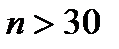 .
.