Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 7. Аналитический методСодержание книги
Поиск на нашем сайте
Построим диаграмму качества переходного процесса по коэффициенту усиления разомкнутой системы
Согласно структурно-математической схеме (см. рис. 3) передаточная функция гармонически линеализованной разомкнутой системы равна:
где -коэффициент гармонической линеализации для релейной характеристики с зоной нечувствительности. По передаточной функции (7.1) определяем характеристический полином замкнутой нелинейной системы
Для построения диаграммы качесвта в полиноме (7.2) произведём подстановку
где индекс Из (7.2) находим
Подставим выражения (7.4) и (7.3), и выделим в последнем вещественную и мнимую части и приравняем их к нулю. Получим
Из второго уравнения (7.5) находим
В выражение (7.6) подставим численные значения параметров. Получим:
Задаемся различными значениями колебаний a и при выбранных постоянных значениях показателей затухания
Рис.5. Диаграмма качества переходного процесса в САУ температуры
Как видно из графиков все кривые расположены левее прямой, проходящей через точку k=0,075. Следовательно, САУ температуры находится в устойчивом равновесном состоянии.
Раздел 8. Частотный метод Коэффициент затухания
где
в результате которой получаем:
Уравнение (4.1) будем решать графически. Для этого в передаточной функции линейной части системы:
произведем подстановку
Модуль этой функции
и фаза
Подставив в выражения (8.7) и (8.8) приведенные в исходных данных значения параметров и, задаваясь различными постоянными значениями показателя затухания На этом же графике нанесем обратную амплитудно-фазовую характеристику нелинейного звена
Рис. 6. Частотные характеристики линейной части системы
Рис. 7. Частотные характеристики линейной части системы и нелинейного звена САУ температуры Как видно из графиков, точка пересечения годографов линейной части системы и нелинейного звена отсутствует. Следовательно, САУ температуры находится в устойчивом равновесном состоянии.
|
||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.005 с.) |

 при отключенной местной ОС (
при отключенной местной ОС (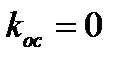 ).
).

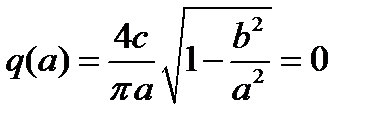

 Эту подстановку удобно выполнять путем разложения полинома D(p,a) в ряд по степеням
Эту подстановку удобно выполнять путем разложения полинома D(p,a) в ряд по степеням  :
:
 означает, что в выражения для производных необходимо подставить
означает, что в выражения для производных необходимо подставить 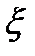 вместо p.
вместо p.
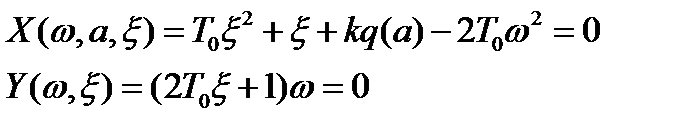
 . Подставим это значение в первое уравнение системы (7.5) и решим его относительно k:
. Подставим это значение в первое уравнение системы (7.5) и решим его относительно k:
 ?????????
????????? строим кривые
строим кривые  (см. рис.5). Кривые
(см. рис.5). Кривые  соответствуют расходящимся колебаниям, а кривые
соответствуют расходящимся колебаниям, а кривые  - затухающим колебаниям. Область, лежащая правее штриховой прямой, проходящей через точку k1, является областью существования автоколебаний. Область, расположенная левее этой прямой, является областью устойчивого равновесного состояния системы.
- затухающим колебаниям. Область, лежащая правее штриховой прямой, проходящей через точку k1, является областью существования автоколебаний. Область, расположенная левее этой прямой, является областью устойчивого равновесного состояния системы.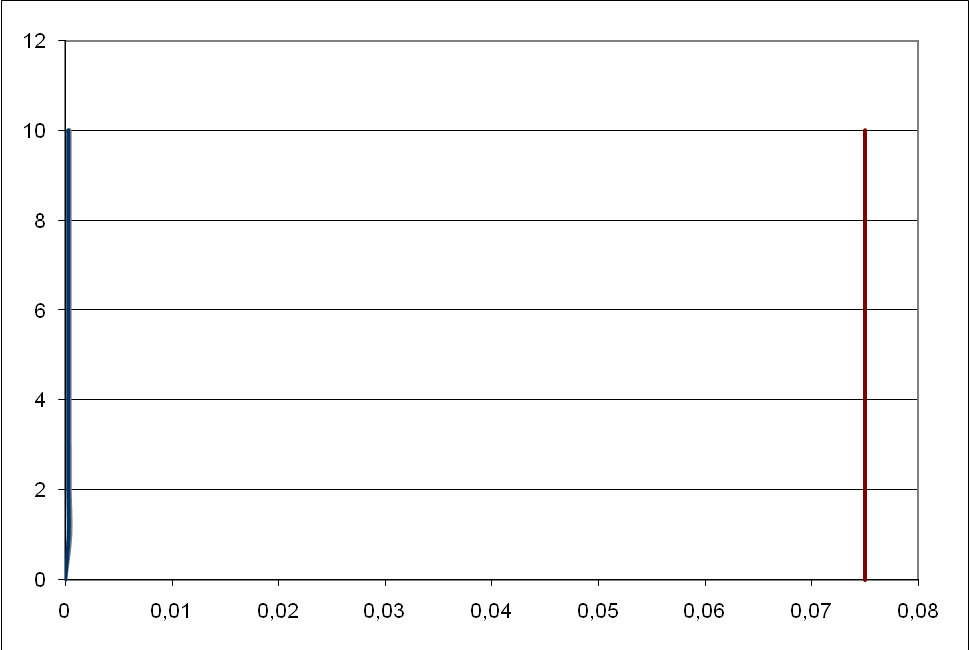
 и частоту колебаний
и частоту колебаний  переходного процесса в САУ температуры будет отыскивать путем решения гармонически линеаризованного уравнения.
переходного процесса в САУ температуры будет отыскивать путем решения гармонически линеаризованного уравнения.

 получается из передаточной функции линейной части системы
получается из передаточной функции линейной части системы  подстановкой
подстановкой  а гармонически линеаризованная передаточная функция нелинейного звена
а гармонически линеаризованная передаточная функция нелинейного звена 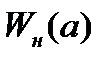 – подстановкой
– подстановкой  в выражение
в выражение
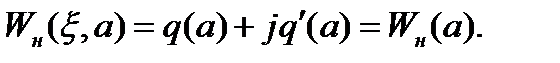

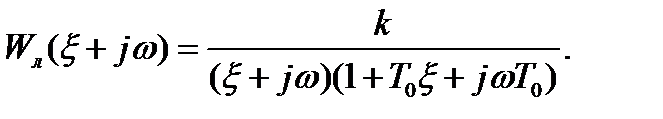


 как функции от частоты колебаний
как функции от частоты колебаний  при
при  (см. рис 6).
(см. рис 6). при заданных параметрах b и с. Для нелинейной характеристики релейного типа с зоной нечувствительности имеем
при заданных параметрах b и с. Для нелинейной характеристики релейного типа с зоной нечувствительности имеем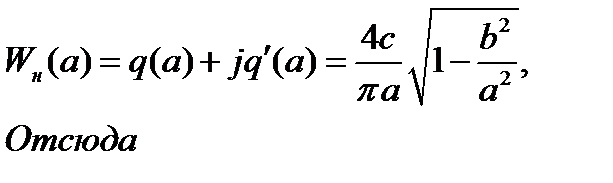
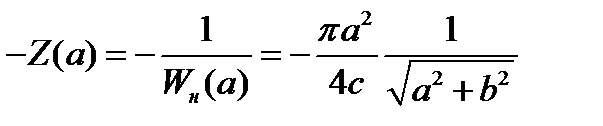 ??????
??????