
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тело, относительно которого определяется положение других тел, связанная с ним система координат и часы для измерения времени образуют пространственно–временную систему отсчета.Содержание книги
Поиск на нашем сайте
2. Мгновенная скорость и ускорение точки:
3. Средняя скорость vср — это скалярная величина, равная отношению пути S, пройденного за время t, к этому промежутку времени:
4. Закон равномерного прямолинейного движения:
В проекции на направление движения (ось х) закон движения принимает вид x=x 0 +v х t, 5. Закон равнопеременного движения:
В проекции на направление движения (ось х) закон движения принимает вид:
vx=vox+axt Траекто́рия материа́льной то́чки — линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта. Если построить траекторию движения тела, брошенного горизонтально, в системе координат xy, приняв за начало отсчета координат точку бросания, а направление оси ординат совпадающим с направлением вектора ускорения свободного падения, то координаты каждой точки P траектории представляют собой перемещение тела в горизонтальном направлении (движение с постоянной скоростью v0) и в вертикальном направлении (равномерно ускоренное движение с ускорением g):
x, y — координаты тела, Так как ускорение свободного падения g и начальная скорость тела v0 — постоянные величины, то координата y пропорциональна квадрату x, т.е. траектория движения представляет собой параболу, вершина которой находится в начальной точке движения. Путь — длина участка траектории материальной точки. Перемеще́ние — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Кинематика Криволинейного движения точки и Движения твердого тела
1. Полное мгновенное ускорение Вектор полного ускорения можно разложить на две составляющие: тангенциальное (касательное) ускорение Тангенциальное ускорение
Нормальное ускорение
Модуль полного ускорения равен:
2. Мгновенное угловое ускорение при движении точки по окружности и при вращении твердого тела вокруг неподвижной оси:
Принцип относительности Галилея: законы механики выглядят одинаково во всех ИСО. При́нцип суперпози́ции: результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.43.106 (0.009 с.) |


 , где
, где  — радиус–вектор точки.
— радиус–вектор точки.
 ,
, 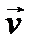 = const,где
= const,где  — радиус–вектор в начальный момент времени t= 0.
— радиус–вектор в начальный момент времени t= 0.
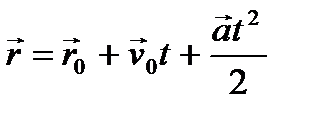 ,
,  ,где
,где  — радиус–вектор и скорость точки в начальный момент времени t = 0 (начальные условия).
— радиус–вектор и скорость точки в начальный момент времени t = 0 (начальные условия).

 .
. и нормальное (центростремительное) ускорение
и нормальное (центростремительное) ускорение  (см. рис. 2.1).
(см. рис. 2.1). =
=  .
. =
=  .(R - радиус кривизны)
.(R - радиус кривизны) .
.



