
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение динамики вращат. Движения
Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение(основной закон динамики вращательного движения).Математически он выражается так: M= 1. Момент инерции Iz системы материальных точек относительно оси Z: Момент инерции твердого тела относительно оси Z: 3. Кинетическая энергия и момент импульса тела, вращающегося с угловой скоростью w вокруг неподвижной оси Z:
Свободное вращение твердого тела. Под свободным движением твердого тела понимают движение, происходящее в от-сутствие внешних сил. Этот простейший вид движения принято называть «движением по инерции». Моменты инерции некоторых сложных тел:
В других случаях для определения момента инерции следует использовать теорему Штейнера: Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных), необходимых для полного описания движения механической системы.Также число степеней свободы равно полному числу независимых уравнений второго порядка или половине числа уравнений первого, полностью описывающих динамику системы. Кинематическая энергия сложного движения.Упругий и неупругий удар. При сложном движении твердого тела его кинетическая энергия может быть представлена в виде суммы кинетических энергий поступательного и вращательного движений.Это относится и к плоскому движению твердого тела. Для вычисления кинетической энергии тела при плоском движении удобно пользоваться формулой
Здесь М – масса твердого тела, V – скорость его центра масс, I – момент инерции относительно оси, проходящей через центр масс, и w – угловая скорость вращения. Эта формула справедлива только тогда, когда ось вращения проходит через центр масс тела.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.69.152 (0.004 с.) |
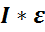 .
. ,где mi - массы точек, ri - их расстояния до оси Z.
,где mi - массы точек, ri - их расстояния до оси Z. ,где интегрирование производится по всему объему тела. Моменты инерции некоторых тел относительно оси Z, проходящей через центр масс (m – масса тела):· диск радиуса R (ось Z перпендикулярна плоскости диска):
,где интегрирование производится по всему объему тела. Моменты инерции некоторых тел относительно оси Z, проходящей через центр масс (m – масса тела):· диск радиуса R (ось Z перпендикулярна плоскости диска):  ;· шар радиуса R:
;· шар радиуса R:  ;· тонкий стержень длины l (ось Z перпендикулярна стержню):
;· тонкий стержень длины l (ось Z перпендикулярна стержню):  .2. Теорема Штейнера. Пусть IC - момент инерции тела относительно оси СС, проходящей через центр масс. Момент инерции IA относительно оси АА, параллельной оси СС и отстоящей от нее на расстояние d, равен:
.2. Теорема Штейнера. Пусть IC - момент инерции тела относительно оси СС, проходящей через центр масс. Момент инерции IA относительно оси АА, параллельной оси СС и отстоящей от нее на расстояние d, равен:  ,где m – масса тела.
,где m – масса тела. ,
,  .
.











