
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двулучепреломление в одноосных кристаллахСодержание книги Поиск на нашем сайте
Пространственное распределение показателя преломления анизотропной среды можно представить с помощью эллипсоида волновых нормалей, полуоси которого равны главным значениям показателя преломления (рис. 6.6). Построим сечение этого эллипсоида плоскостью, перпендикулярной волновому вектору k. Это сечение представляет собой эллипс, направления осей которого определяют направления векторов D' и D" двух распространяющихся в кристалле волн, а длины полуосей пропорциональны показателям преломления этих волн. Известно, что любой трехосный эллипсоид имеет два центральных круговых сечения. Направления, перпендикулярные этим сечениям и есть направления оптических осей кристалла.
На рис. 6.7 представлены эллипсоиды нормалей для двух возможных случаев: а) – скорость обыкновенного луча меньше, чем необыкновенного (no > ne, отрицательный кристалл), и б) –скорость обыкновенного луча больше, чем необыкновенного (no < ne, положительный кристалл). В обоих случаях при последовательном изменении направления луча от k 1 до k 5 показатель преломления луча с Y-поляризацией no не изменяется. Показатель преломления необыкновенного луча в первом случае уменьшается от no до ne, а во втором – возрастает. Точечной заливкой выделены главные плоскости. Найдем зависимость фазовой скорости световой волны в одноосном кристалле от направления распространения. Уравнение волновых нормалей (6.6) при Vx = Vy = Vo, Vz = Ve можно переписать в виде
Направление нормали удобно задавать через угол q с оптической осью. Тогда
Анализ распространения света в кристаллах и преломления на границах становится наглядным при использовании сечений волновых поверхностей (рис. 6.8). При этом в плоскости рисунка изображаются “мгновенные” сечения волновых фронтов обыкновенной и необыкновенной волн, испущенных точечным источником, помещенным в начало координат. Для первого они сферические, а для второго – представляют овалоид вращения, описываемый вторым уравнением (6.8). Направление, в котором эти сечения совпадают (т. е. обыкновенная и необыкновенная волны распространяются с одинаковой скоростью Vo), и является оптической осью кристалла.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.108.8 (0.009 с.) |

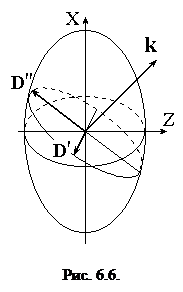 В одноосном кристалле эллипсоид нормалей превращается в эллипсоид вращения вокруг оси Z, его единственное круговое сечение лежит в плоскости XY. Для одноосных кристаллов принято обозначать главные показатели преломления nz º ne, nx = ny º no.
В одноосном кристалле эллипсоид нормалей превращается в эллипсоид вращения вокруг оси Z, его единственное круговое сечение лежит в плоскости XY. Для одноосных кристаллов принято обозначать главные показатели преломления nz º ne, nx = ny º no.
 . (6.7)
. (6.7) ,
,  и решениями уравнения (6.7) являются
и решениями уравнения (6.7) являются (6.8)
(6.8)



