
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распространение монохроматической плоской волны в анизотропной средеСодержание книги
Поиск на нашем сайте Рассмотрим геометрические соотношения между основными векторами в электромагнитной волне. Уравнения (4.1), остаются справедливыми и в анизотропных средах. Введем единичный вектор нормали к волновому фронту N = k / k, тогда (4.1) можно переписать в виде:
Направление переноса энергии в волне определяется вектором Пойнтинга D ^ H, D ^ N, N ^ H, s ^ E, s ^ H, E ^ H. (6.4)
Соотношение между фазовой и лучевой скоростями можно получить, рассматривая два положения волнового фронта, соответствующие двум близким моментам времени (рис. 6.3). Из-за анизотропии среды форма волновой поверхности отлична от сферической (более подробно этот вопрос обсуждается в следующем разделе). Направление фазовой скорости совпадает с направлением волновой нормали N, а направление лучевой – с лучевым вектором s, проведенным от источника О в точку наблюдения. Из рисунка видно, что фазовая скорость равна проекции лучевой на направление волновой нормали:
Различие фазовой и лучевой скоростей является проявлением пространственной дисперсии (см. раздел 2.1). Эти скорости отличаются даже для монохроматических волн, а также в отсутствие временной дисперсии n ¹ n (l). Исключая из уравнений (6.3) напряженность магнитного поля и учитывая соотношения (6.2) можно получить выражение для скорости волны, распространяющейся в кристалле с главными скоростями Vx > Vy > Vz в направлении вектора N с проекциями (Nx, Ny, Nz), называемое уравнением волновых нормалей Френеля:
Попадая в кристалл, произвольная световая волна распадается на две ортогонально поляризованные волны с разными скоростями и разными направлениями переноса энергии – возникает двойное лучепреломление. Следует отметить, что в ряде случаев лучевые вектора этих волн могут совпадать (a = 0), например, при распространении волны вдоль любой из главных осей кристалла. При определенном выборе направления распространения, а именно
два решения уравнения Френеля совпадают, т. е. V ' = V ''. Такие направления (O'O' и O"O" на рис. 6.5) называются оптическими осями кристалла, а сам кристалл называется двухосным. Если Vx = Vy ¹ Vz, то обе оптические оси сливаются с осью Z. Такой кристалл называется одноосным.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.66.158 (0.009 с.) |

 . (6.3)
. (6.3) . Определим лучевой вектор как s = S / S. Из свойств векторного произведения следует, что
. Определим лучевой вектор как s = S / S. Из свойств векторного произведения следует, что Поскольку вектора D и E в анизотропной среде неколлинеарны, приходим к выводу, что в волне существуют две правые ортогональные тройки векторов (E, H, s) и (D, H, N), повернутые на угол a относительно общего вектора H (рис. 6.2). Таким образом, направление перемещения волнового фронта (вектор N) в кристаллах в общем случае не совпадает с направлением переноса энергии (вектор s). Соответственно различают фазовую скорость V (скорость перемещения фронта) и лучевую скорость u (скорость переноса энергии).
Поскольку вектора D и E в анизотропной среде неколлинеарны, приходим к выводу, что в волне существуют две правые ортогональные тройки векторов (E, H, s) и (D, H, N), повернутые на угол a относительно общего вектора H (рис. 6.2). Таким образом, направление перемещения волнового фронта (вектор N) в кристаллах в общем случае не совпадает с направлением переноса энергии (вектор s). Соответственно различают фазовую скорость V (скорость перемещения фронта) и лучевую скорость u (скорость переноса энергии).
 . (6.5)
. (6.5) . (6.6)
. (6.6)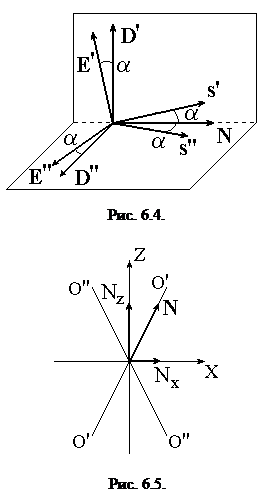 Уравнение волновых нормалей может быть преобразовано к квадратному уравнению относительно фазовой скорости V, и, следовательно, имеет два корня. Таким образом, в каждом направлении в кристалле могут распространяться две волны с различными фазовыми скоростями V' и V'' и ортогональными поляризациями D ' ^ D ''. Каждому вектору D соответствует свой вектор E, повернутый на угол a, а каждому вектору E – ортогональный ему лучевой вектор s (рис. 6.4).
Уравнение волновых нормалей может быть преобразовано к квадратному уравнению относительно фазовой скорости V, и, следовательно, имеет два корня. Таким образом, в каждом направлении в кристалле могут распространяться две волны с различными фазовыми скоростями V' и V'' и ортогональными поляризациями D ' ^ D ''. Каждому вектору D соответствует свой вектор E, повернутый на угол a, а каждому вектору E – ортогональный ему лучевой вектор s (рис. 6.4). ,
,


