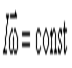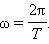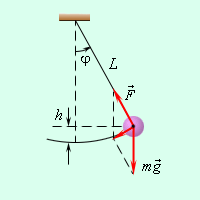Работа, мощность и кинетическая энергия при вращательном движении. Законы сохранения момента импульса и кинетической энергии замкнутой системы.

Затухающие колебания. Уравнения кинематики и динамики. Графическое представление. Силы сопротивления.

В реальных условиях любая механическая система находится под действием сил трения (сопротивления). При этом часть механической энергии превращается во внутреннюю энергию теплового движения, и свободные колебания становятся затухающими(колебания, амплитуда которых уменьшается вследствие потерь энергии системой).

Рисунок 1.9.6. График затухающих колебаний.

Затухание вызывается силой, которая пропорциональна скорости и направлена противоположно ей:

.

F ~ −υ

Коэффициент пропорциональности называют коэффициентом вязкого трения β, т. е.

F = −βυ = −βy, где y – отклонение, β – коэффициент вязкого трения.

 

 

Вынужденные колебания. Уравнения кинематики и динамики. Вынуждающая сила. Графики. Резонанс.

Вынужденные колебания – колебания, возникающие под действием внешней периодически изменяющейся силы. Частота вынужденных колебаний равна частоте изменения внешней силы.

Если частота ν внешней силы совпадет с частотой свободных колебаний системы, то амплитуда колебаний резко возрастает. Это явление называется резонансом.

Резонанс – резкое возрастание амплитуды колебаний. Вынуждающая сила - сила, вынуждающая что-то делать

Ое начало термодинамики. (для теплового двигателя). Схемы идеальной тепловой машины и холодильника. КПД идеальной тепловой машины.

Второе начало термодинамики позволяет определить направление протекания процессов.

 

Работа, мощность и кинетическая энергия при вращательном движении. Законы сохранения момента импульса и кинетической энергии замкнутой системы.

При вращательном движении работа определяется проекцией момента сил на направление угловой скорости:

кинетическая энергия при вращательном движении

мощность при вращательном движении

 

Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.
Поэтому, то есть

или

Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Это один из фундаментальных законов природы.

Закон сохранения механической энергии:

Ek1 + Ep1 = Ek2 + Ep2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

 

14. Механические колебания. Свободные колебания и его характеристики (возвращающаяся сила, амплитуда, фаза, частота). Уравнения кинематики и динамики свободных колебаний и их графики. Энергия колебаний.

Колебания – это движения или процессы, которые характеризуются определенной повторяемостью во времени

Период колебаний T – интервал времени, в течение которого происходит одно полное колебание

Частота колебаний ν – число полных колебаний в единицу времени. В системе СИ выражается в герцах (Гц).

Амплитуда – максимальное отклонение колеблющейся величины от некоторого усредненного ее значения для системы. (м)

Фаза колебаний – определяет смещение в любой момент времени, то есть определяет состояние колебательной системы

Период и частота колебаний связаны соотношением

Циклическая (или круговая) (она показывает число колебаний за 2п единиц времени) частота ω = 2πν. Она связана с периодом отношением

Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса. Смещение определяется формулой

Свободные колебания – это колебания, происходящие без участия внешнего периодического воздействия.

В качестве примеров свободных колебаний можно привести пружинный и математический маятники. Пружинный (гармонический) маятник – груз массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно. Круговая частота колебаний груза равна

	Рисунок 1.9.4. Пружинный маятник.

а период

 

Рисунок 1.9.5. Математический маятник.

Математический маятник – тело небольших размеров, подвешенное на тонкой нерастяжимой невесомой нити длиной l. Круговая частота математического маятника равна

а период колебаний