
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез кодовой комбинации циклического кодаСодержание книги
Поиск на нашем сайте
Кодовая комбинация циклического кода может быть получена двумя способами. Первый получается умножением информационной последовательности на образующий полином Р (х), что приводит к формированию неразделимого циклического кода. Неразделимость значительно усложняет процесс декодирования. Поэтому на практике чаще используют второй способ, при котором информационная последовательность умножается на одночлен хr и добавляется остаток от деления полученной последовательности на образующий полином. Это можно записать в виде формулы:
где F (x) – кодовая комбинация циклического кода;
G (x) – информационная последовательность в полиномиальной форме;
Для перевода двоичной последовательности в полиномиальную форму каждый бит (1 или 0) умножается на х в степени, соответствующей месторасположению этого бита.
Составление информационная последовательность в полиномиальной форме - G (x)
Необходимо составить информационный блок, состоящий из трех прописных букв – инициалов фамилии, имени и отчества студента. Для составления необходимо использовать фрагмент кодовой таблицы первичного кода КОИ-8, который представлен на рис. 1.
Старшие биты считываются из первых четырех строк, а младшие – из первых четырех столбцов, соответствующих месторасположению буквы на рисунке.
Рисунок 1 – Код КОИ-8. Фрагмент русского алфавита
Закодированные инициалы Бойко Иван Владимирович: Б ® 1011 0001 И ® 1011 1000
В ® 1011 0010 Переведем последовательность в полиномиальную форму.
Полученную кодовую комбинацию можно записать как: G (x) = х 23 + х 21 + х 20 + х 16 + х 15 + х 13 + х 12 + х 11 + х 7 + х 5 + х 4 + х 1 Умножим G (x) на одночлен хr. Так как количество проверочных разрядов, рассчитанное в п. 1.2 равно восьми, то умножаем на х 14
G(x) х 14 = х 37 + х 35 + х 34 + х 30 + х 29 + х 27 + х 26 + х 25 + х 21 + х 19 + х 18+ х 15
Для получения разрешенной комбинации циклического кода разделим полученную последовательность на выбранный в п. 1.2 образующий полином. Процесс деления показан ниже.
Итак, разрешенная комбинация циклического кода, в соответствии с формулой (7) имеет вид:
F (x)= х 31 + х 30 + х 24 + х 23 + х 22 + х 16 + х 15 + х 14 + х 11 + х 10 + х 9 + х 7 + х 6 + x 4 + x 3 + x.
Переведем ее в двоичный вид:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.213.208 (0.009 с.) |

 (7)
(7)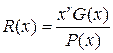 - остаток от деления на образующий полином.
- остаток от деления на образующий полином.






