
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изменение координат вектора при изменении базисаСодержание книги
Поиск на нашем сайте
Пусть в
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса
Эта матрица называется матрицей перехода от старого базиса к новому. Изменение матрицы линейного преобразования при изменении базиса В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой. Пусть Предложение 19.1 Пусть
Доказательство. Пусть Определение 19.2 Две квадратных матрицы Следствие 19.1 Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах. Напомним, что в евклидовом пространстве определено скалярное произведение векторов
Определение. Если существует такой оператор B,что для любых Теорема. Если A — линейный оператор в евклидовом пространстве E и A — его матрица в некотором ортонормированном базисе в E, то у оператора есть единственный сопряженный оператор, причем матрица сопряженного оператора в том же базисе — это матрица AT. Теорема доказана на лекции. Пример. Рассмотрим оператор Uj поворота пространства R2 на угол j относительно начала координат против часовой стрелки:
Матрицы операторов поворота на угол j и угол - j имеют, соответственно, вид:
Нетрудно доказать (на лекции доказано) следующие свойства сопряженного оператора: · что сопряженный к линейному оператру — линейный оператор; · · · · характеристические многочлены операторов совпадают. 5.3.2. Самосопряженный оператор Определение. Если линейный оператор A, действующий в евклидовом пространсте E, таков, что для любых Пример. Оператор P2 — оператор проектирования пространства R3 на подпространство R2 параллельно вектору Как показано выше, матрица оператора P 2 в естественном ортонормированном базисе Имеет вид
Тогда
Видно, что матрица P2 оператора P 2 — симметричная матрица. Нетрудно доказать следующие свойства самосопряженного оператора: · сумма самосопряженных операторов — самосопряженный оператор; · если оператор A самосопряженный оператор, то оператор 5.3.3. Собственные значения и собственные векторы самосопряженного оператора Можно показать (на лекции не доказывается), что у самосопряженного оператора существует собственный ортонормированный базис. Поскольку A=A*, то матрица самосопряженного оператора — симметричная матрица. Справедлива следующая теорема.
Теорема. Матрица самосопряженного оператора в собственном базисе имеет диагональную форму. Ясно, что для того чтобы привести матрицу самосопряженного оператор к диагональному виду нужно найти собственные значения оператора и диагональную матрицу, на диагонали которой расположены собственные значения матрицы. Если нужно записать выражение для приведения матрицы к этой диагональной форме, то нужно еще найти собственные векторы матрицы, записать матрицу C перехода к собственному базису (матрицу, столбцами которой являются координаты собственных векторов оператора), найти обратную к ней матрицу С -1 и тогда
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.71.60 (0.01 с.) |

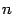 -мерном линейном пространстве
-мерном линейном пространстве 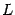 выбран базис
выбран базис 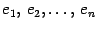 , который мы будем для удобства называть "старый" и другой базис
, который мы будем для удобства называть "старый" и другой базис 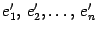 , который мы будем называть "новый". Возьмем призвольный вектор
, который мы будем называть "новый". Возьмем призвольный вектор 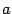 из
из 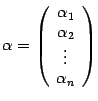 , а в новом --
, а в новом -- 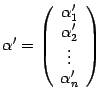 . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису
. Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису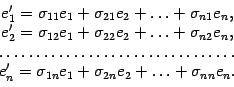

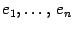 и
и 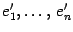 -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть
-- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть 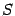 -- матрица перехода 19.1.4 а от старого базиса к новому.
-- матрица перехода 19.1.4 а от старого базиса к новому.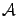 -- линейное преобразование пространства
-- линейное преобразование пространства 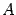 и
и 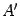 -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда
-- матрицы этого преобразования в старом и новом базисе соответственно. Тогда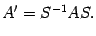
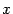 -- произвольный вектор пространства
-- произвольный вектор пространства 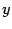 -- его образ, то есть
-- его образ, то есть 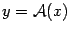 . Пусть
. Пусть 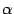 и
и 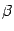 -- координатные столбцы векторов
-- координатные столбцы векторов 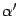 ,
, 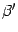 -- в новом. Тогда в силу формулы (19.3)
-- в новом. Тогда в силу формулы (19.3) 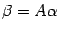 . По предложению 18.5 имеем
. По предложению 18.5 имеем 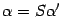 ,
, 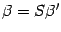 . Подставим эти выражения в предыдущую формулу, получаем
. Подставим эти выражения в предыдущую формулу, получаем 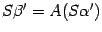 . Откуда
. Откуда 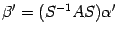 . С другой стороны, в силу формулы (19.3) в новом базисе
. С другой стороны, в силу формулы (19.3) в новом базисе 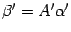 . Сравнивая это равенство с предыдущим, получаем
. Сравнивая это равенство с предыдущим, получаем 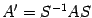 .
.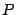 и
и 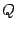 одного порядка называются подобными, если существует такая невырожденная матрица
одного порядка называются подобными, если существует такая невырожденная матрица 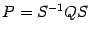 .
.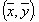
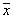 и
и 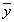 из евклидова пространства E справедливо
из евклидова пространства E справедливо 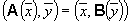 , то оператор B называется сопряженным оператором к оператору A и обозначается A*:
, то оператор B называется сопряженным оператором к оператору A и обозначается A*: 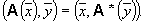
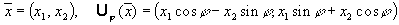
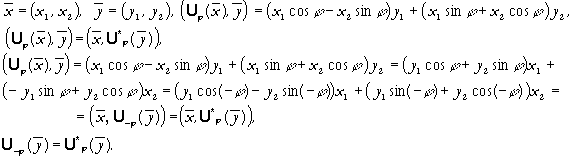
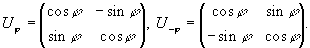 Видно, что
Видно, что 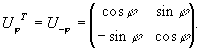
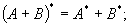
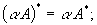
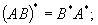
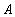 и
и 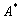
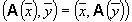 , то оператор A называется самосопряженным оператором.
, то оператор A называется самосопряженным оператором.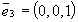 :
: 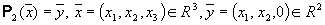 .
.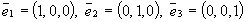
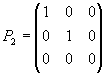
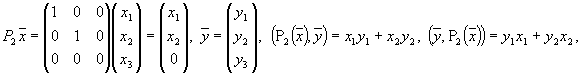 т.е.
т.е. 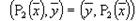 — оператор P 2 — самосопряженный оператор.
— оператор P 2 — самосопряженный оператор.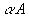 — тоже самосопряженный оператор (
— тоже самосопряженный оператор (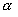 — действительное число).
— действительное число).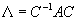 — равенство, связывающее диагональну форму
— равенство, связывающее диагональну форму 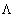 матрицы оператора в собственном базисе с матрицей A оператора в заданном базисе.
матрицы оператора в собственном базисе с матрицей A оператора в заданном базисе.


