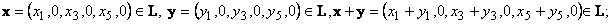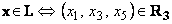Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители.( детерминанты)Содержание книги
Поиск на нашем сайте
Определение. Определителем квадратной матрицы А= det A = М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов. Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу: det A = Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула: detA =
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1. Для указанной матрицы А число М1к называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах. Обратная матрица Определим операцию деления матриц как операцию, обратную умножению.
Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию: XA = AX = E, где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну. Рассмотрим общий подход к нахождению обратной матрицы. Исходя из определения произведения матриц, можно записать: AX = E Þ eij = 0, i ¹ j, eij = 1, i = j. Таким образом, получаем систему уравнений:
Решив эту систему, находим элементы матрицы Х. Пример. Дана матрица А =
Таким образом, А-1=
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
где Мji - дополнительный минор элемента аji матрицы А.
Пример. Дана матрица А = det A = 4 - 6 = -2.
M11=4; M12= 3; M21= 2; M22=1 x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким образом, А-1=
Cвойства обратных матриц Укажем следующие свойства обратных матриц: 1) (A-1)-1 = A;
2) (AB)-1 = B-1A-1
3) (AT)-1 = (A-1)T. Пример. Дана матрица А = А2 = АА =
Отметим, что матрицы
Пример. Вычислить определитель
Значение определителя: -10 + 6 – 40 = -44.
Ранг матрицы Определение. Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров. Т.е. если у матрицы порядка (m, n) есть отличный от нуля минор порядка r, r<= min(m, n), а все миноры более высоких порядков равны нулю, то r — ранг матрицы. Очень важным свойством элементарных преобразований матриц является то, что они не изменяют ранг матрицы. Элементарные преобразования матрицы Определение. Элементарными преобразованиями матрицы назовем следующие преобразования: 1) умножение строки на число, отличное от нуля; 2) прибавление к элемнтам одной строки элементов другой строки; 3) перестановка строк; 4) вычеркивание (удаление) одной из одинаковых строк (столбцов); 5) транспонирование; Те же операции, применяемые для столбцов, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк (столбцов). . РАНГ СТУПЕНЧАТОЙ МАТРИЦЫ РАВЕН ЧИСЛУ ЕЕ СТРОК Арифметическим вектором называется упорядоченная совокупность n чисел. Обозначается x = (x 1, x 2,..., xn); числа x 1, x 2, ..., xn называются компонентами арифметического вектора. Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: для любых x = (x 1, x 2,..., xn), y = (y 1, y 2,..., yn) и любого числа α справедливо: x + y = (x 1+ y 1, x 2 + y 2,..., xn + yn);α x = (αx 1, αx 2,..., α xn). Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn. Вектор θ = (0, 0,..., 0) называется нулевым вектором Rn, а вектор − x = (−x 1, −x 2,..., −xn) — противоположным вектором для вектора x в Rn. Для любых векторов x, y и z из Rn и любых чисел α и β справедливо: 1. x + y = x + y, сложение коммутативно; 2. x + (y + z) = (x + y)+ z, сложение ассоциативно; 3. x + θ = x;
4. x + (− x) = θ; 5. α(x + y) = α x + α y, умножение на число дистрибутивно относительно сложения векторов; 6. α(β x) = (αβ) x, умножение на число ассоциативно; 7. (α + β) x = α x + β x, умножение вектора на число дистрибутивно относительно сложения чисел. 8. 1· x = x. Пространство Rn − n -мерное векторное пространство, dim Rn = n. Если в пространстве Rn определен естественный базис e 1, e 2,... e n , e 1= (1, 0, 0,..., 0, 0), e 2= (0, 1, 0,..., 0, 0),..., e n -1= (0, 0, 0,..., 1, 0), e n = (0, 0, 0,..., 0, 1), то компоненты вектора x = (x 1, x 2,..., x n) из Rn являются координатами вектора x в естественном базисе e 1, e 2,... e n: x = (x 1, x 2,..., x n) = x 1 e 1+ x 2 e 2+...+ x n e n. Всякое конечномерное n -мерное линейное пространство изоморфно пространству арифметических векторов Rn. Пример L − множество 6-мерных арифметических векторов, у которых чётные коомпоненты равны нулю, {x =(x1, 0, x2, 0, x5, 0) } − трёхмерное линейное пространство, изоморфное пространству арифметических векторов R3. Действительно.
Как видно из приведенных выше соотношений, множество L − трёхмерное линейное пространство (три вектора e1, e2 и e3 образуют базис), изоморфное пространству трёхмерных арифметических векторов R3.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.42.19 (0.011 с.) |

 называется число, которое может быть вычислено по элементам матрицы по формуле:
называется число, которое может быть вычислено по элементам матрицы по формуле: , где
, где
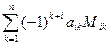 , i = 1,2,…,n.
, i = 1,2,…,n. , i=(1,n), j=(1,n),
, i=(1,n), j=(1,n), ,
, , найти А-1.
, найти А-1.


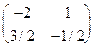 .
.
 , найти А3.
, найти А3. ; A3 =
; A3 =  .
. .
.
 = -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10. =
=  = 2(0 – 2) – 1(0 – 6) = 2.
= 2(0 – 2) – 1(0 – 6) = 2. =
=  = 2(-4) – 3(-6) = -8 + 18 = 10.
= 2(-4) – 3(-6) = -8 + 18 = 10.